Conceito de experimento aleatório, espaço de amostra, exemplos

Fala -se de experimento aleatório Quando o resultado de cada estudo em particular é imprevisível, mesmo quando a probabilidade de ocorrência de um determinado resultado pode ser estabelecida.

No entanto, deve -se esclarecer que não é possível reproduzir o mesmo resultado de um sistema aleatório com os mesmos parâmetros e condições iniciais em cada estudo do experimento.

figura 1. O lançamento de dados é um experimento aleatório. Fonte: Pixabay.

Um bom exemplo de experimento aleatório é o lançamento de um dado. Mesmo quando você tome cuidado para lançar os dados da mesma maneira, em cada tentativa, um resultado imprevisível será obtido. Na verdade, a única coisa que pode ser afirmada é que o resultado pode ser alguns dos seguintes: 1, 2, 3, 4, 5 ou 6.

O lançamento de uma moeda é outro exemplo de experimento aleatório com apenas dois resultados possíveis: face ou selo. Embora a moeda seja lançada a partir da mesma altura e da mesma maneira, o fator de chance estará sempre presente, o que resulta em incerteza para cada nova tentativa.

O oposto de um experimento aleatório é um experimento determinístico. Por exemplo, sabe -se que toda vez que a água é fervida no nível do mar, a temperatura de ebulição é 100 ºC. Mas nunca acontece que, mantendo as mesmas condições, o resultado às vezes é 90 ºC, outros 12 0ºC e às vezes 100 ºC.

[TOC]

Espaço amostral

O conjunto de todos os resultados possíveis de um experimento aleatório é chamado espaço amostral. No experimento aleatório do lançamento de um dado, o espaço de amostra é:

D = 1, 2, 3, 4, 5, 6.

Por sua parte, no lançamento de uma moeda, o espaço de amostra é:

M = face, selo.

Evento ou evento

Em um experimento aleatório, um evento É a ocorrência ou não de um certo resultado. Por exemplo, no caso do lançamento de uma moeda, um evento ou evento é para ser caro.

Pode atendê -lo: lados homólogos

Outro evento em um experimento aleatório pode ser o seguinte: o lançamento de um número de um número menor que três é liberado.

Caso o caso ocorra, o conjunto de resultados possíveis é o conjunto:

E = 1, 2, 3

Por sua vez, este é um subconjunto do espaço ou conjunto de amostras:

M = 1, 2, 3, 4, 5, 6.

Exemplos

Abaixo estão alguns exemplos que ilustram os acima:

Exemplo 1

Suponha que duas moedas sejam jogadas, uma após a outra. É solicitado:

a) indicar se é um experimento aleatório ou pelo contrário um experimento determinístico.

b) Qual é o espaço de amostra deste experimento?

c) Indique todo o evento A, correspondente ao experimento, tem um resultado de rosto e carimbo.

d) Calcule a probabilidade de que o evento ocorra para.

e) Finalmente, encontre a probabilidade de que o evento B: não pareça cara ao resultado.

Solução 

a) É um experimento aleatório, porque não há como prever o que será o resultado de um lançamento das duas moedas.

b) O espaço da amostra é o conjunto de todos os resultados possíveis:

S = (c, c), (c, s), (s, c), (s, s)

c) O evento A, no caso que é dado, pode ter os seguintes resultados:

A = (c, s), (s, c)

d) A probabilidade de evento A é obtida ao dividir o número de elementos do conjunto A entre o número de elementos do conjunto correspondente ao espaço da amostra:

P (a) = 2/4 = ½ = 0.5 = 50%

e) O conjunto de resultados possíveis correspondentes ao evento B (não aparecendo face ao resultado) é:

Pode atendê -lo: trinômio quadrado perfeito

B = (s, s)

Portanto, a probabilidade de o evento B ocorrer em um ensaio é a razão entre o número de resultados possíveis de B entre o número de casos totais:

P (b) = ¼ = 0.25 = 25%.

Exemplo 2

Uma bolsa contém 10 bolinhas brancas e 10 bolinhas pretas. Da bolsa, eles são removidos aleatoriamente e sem olhar para dentro de três bolinhas consecutivamente. 

a) Determine o espaço da amostra deste experimento aleatório.

b) Determine o conjunto de resultados correspondentes ao evento que é que, após o experimento, existem dois bolinhas pretas.

c) O evento B deve obter pelo menos dois bolinhas pretas, determinar o conjunto B dos resultados para este evento.

d) Qual é a probabilidade de o evento ocorrer?

e) Encontre a probabilidade de que o evento B.

f) determinar a probabilidade de que o resultado do experimento aleatório seja que pelo menos um mármore preto. Este evento será chamado de C.

Figura 2. Bolinhas pretas e pretas para experimentos aleatórios. Fonte: NeedPix.

Solução para

Para construir o espaço da amostra, é útil fazer um diagrama de árvore, como o mostrado na Figura 3:

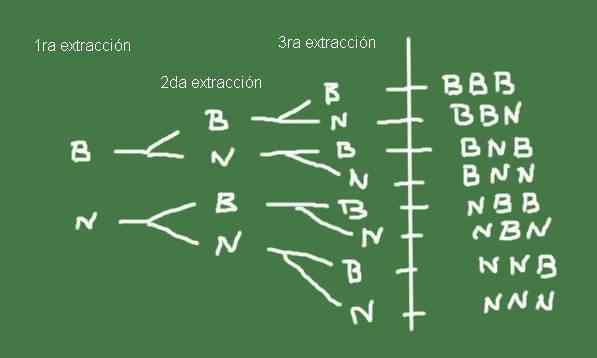Figura 3. Diagrama de árvores por exemplo 2. Preparado por Fanny Zapata.

O conjunto ω de resultados possíveis de extrair três mármores de uma bolsa com o mesmo número de bolinhas pretas e pretas é precisamente o espaço de amostra deste experimento aleatório.

Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)

Solução b

O conjunto de resultados possíveis correspondentes ao evento A, que consiste em ter duas bolinhas de gude pretas é:

Pode atendê -lo: Soma de Riemann: História, fórmulas e propriedades, exercícios

A = (b, n, n), (n, b, n), (n, n, b)

Solução c

O evento B é definido como: "Ter pelo menos duas bolinhas de gude pretas depois de fazer a extração aleatória de três deles". O conjunto de resultados possíveis para o evento B é:

B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)

Solução d

A probabilidade de ter o evento A é a razão entre o número de resultados possíveis para este evento e o número total de resultados possíveis, ou seja, o número de elementos de espaço de amostra.

P (a) = n (a) / n (ω) = 3/8 = 0.375 = 37.5%

Então existem 37.5% de probabilidade de ter dois bolinhas negras depois de extrair aleatoriamente três mármores da bolsa. Mas observe que de forma alguma podemos prever o resultado exato do experimento.

Solução e

A probabilidade de o evento B ser dado, consistindo em pelo menos um mármore preto é:

P (b) = n (b) / n (ω) = 4/8 = 0.5 = 50%

Isso significa que a possibilidade de evento B é igual à probabilidade que não ocorra. 

Solução f

A probabilidade de obter pelo menos um mármore preto, depois de extrair três deles, é igual a 1 menos a probabilidade de que o resultado seja "as três mármores brancos".

P (c) = 1 - p (b b b) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Agora, podemos verificar esse resultado, observando que o número de possibilidades, dado o evento C, é igual ao número de elementos dos possíveis resultados para o evento C:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)

N (c) = 7

P (c) = n (c) / n (ω) = ⅞ = 87.5%

Referências

1. Canalphi. Experimento aleatório. Recuperado de: youtube.com.
2. Mathemovil. Experimento aleatório. Recuperado de: youtube.com
3. Pishro nick h . Introdução à probabilidade. Recuperado de: ProbabilityCourse.com
4. Ross. Probabilidade e estatística para engenheiros. Mc-Graw Hill.
5. Wikipedia. Experiência (teoria da probabilidade). Recuperado de: em.Wikipedia.com
6. Wikipedia. Evento determinístico. Recuperado de: é. Wikipedia.com
7. Wikipedia. Experimento aleatório. Recuperado de: é.Wikipedia.com