Regra empírica como aplicá -la, para que serve, exercícios resolvidos

A Regra empírica É o resultado da experiência prática e da observação da vida real. Por exemplo, você pode saber que as espécies de aves podem ser observadas em certos lugares em cada época do ano e que a observação pode ser estabelecida uma "regra" que descreve os ciclos de vida desses pássaros.

Nas estatísticas, a regra empírica refere -se à forma de agrupamento de observações em torno de um valor central, média ou média, em unidades de desvio padrão.

Suponha que você tenha um grupo de pessoas com uma altura média de 1.62 metros e um desvio padrão de 0.25 metros, então a regra empírica permitiria definir, por exemplo, quantas pessoas estariam em um intervalo da média mais ou menos um desvio padrão?

De acordo com a regra, 68% dos dados são mais ou menos um desvio padrão da média, ou seja, 68% do grupo que as pessoas terão uma altura entre 1.37 (1.62-0.25) e 1.87 (1.62+0.25) metros.

[TOC]

De onde vem a regra empírica?

A regra empírica é uma generalização do teorema de Tchebyshev e distribuição normal.

Teorema de Tchebyshev

O teorema de Tchebyshev diz que: para algum valor de k> 1, a probabilidade de uma variável aleatória estar entre a média menos k vezes o desvio padrão e a média mais K vezes, o desvio padrão é maior ou igual a (1 -1 /k²).

A vantagem desse teorema é que ele se aplica a variáveis ​​aleatórias discretas ou contínuas com qualquer distribuição de probabilidade, mas a regra definida dela nem sempre é muito precisa, porque depende da simetria da distribuição. Quanto mais assimétrica a distribuição da variável aleatória, menos ajustada à regra será seu comportamento.

A regra empírica definida desse teorema é:

Se k = √2, diz -se que 50% dos dados estão no intervalo: [µ - √2 s, µ + √2 s]

Se k = 2, diz -se que 75% dos dados estão no intervalo: [µ - 2 s, µ + 2 s]

Se k = 3, diz -se que 89% dos dados estão no intervalo: [µ - 3 s, µ + 3 s]

Distribuição normal

A distribuição normal, ou Gauss Bell, permite estabelecer a regra empírica ou a regra 68 - 95 - 99.7.

Pode atendê -lo: proporção

A regra é baseada nas probabilidades de ocorrência de uma variável aleatória em intervalos entre a média menos um, dois ou três desvios padrão e a média mais um, dois ou três desvios padrão.

A regra empírica define os seguintes intervalos:

68.27% dos dados estão no intervalo: [µ - s, µ + s]

95.45% dos dados estão no intervalo: [µ - 2s, µ + 2s]

99.73% dos dados estão no intervalo: [µ - 3s, µ + 3s]

Na figura, você pode ver como esses intervalos são apresentados e a relação entre eles, aumentando a largura da base gráfica.

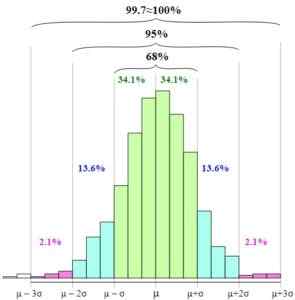Regra empírica. Melikamp [CC BY-SA 4.0 (https: // CreativeCommons.org/)] A padronização da variável aleatória, ou seja, a expressão da variável aleatória em termos da variável padrão ou normal, simplifica o uso da regra empírica, uma vez que a variável z tem média igual a zero e desvio padrão igual para um.

Portanto, a aplicação da regra empírica em escala de uma variável normal padrão, z, define os seguintes intervalos:

68.27% dos dados estão no intervalo: [-1, 1]

95.45% dos dados estão no intervalo: [-2, 2]

99.73% dos dados estão no intervalo: [-3, 3]

Como aplicar a regra empírica?

A regra empírica permite que você abrevie os cálculos ao trabalhar com uma distribuição normal.

Suponha que um grupo de 100 estudantes universitários tenha uma idade média de 23 anos, com um desvio padrão de 2 anos. Que informação a regra empírica permite?

A aplicação da regra empírica implica seguir as etapas:

1- Construir os intervalos da regra

Como a média é 23 e o desvio padrão é 2, os intervalos são:

[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]

[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]

2- Calcule o número de estudantes em cada intervalo de acordo com as porcentagens

(100)*68.27% = 68 alunos aproximadamente

(100)*95.45% = aproximadamente 95 alunos

(100)*99.73% = 100 alunos

3- Intervalos de idades estão associados à quantidade de alunos e interpretados

Pelo menos 68 alunos têm entre 21 e 25 anos.

Pode servir a você: Estatística descritiva: história, características, exemplos, conceitos

Pelo menos 95 alunos têm entre 19 e 27 anos.

Praticamente 100 alunos têm entre 17 e 29 anos.

Qual é a regra empírica para?

A regra empírica é uma maneira rápida e prática de analisar dados estatísticos, sendo cada vez mais confiável na medida em que a distribuição está próxima da simetria.

Sua utilidade depende do campo em que é usado e das perguntas que surgem. É muito útil saber que a ocorrência de valores de três desvios padrão é quase improvável abaixo ou acima da média, mesmo para variáveis ​​de distribuição não normais, pelo menos 88.8% dos casos estão no intervalo de três sigma.

Nas ciências sociais, um resultado geralmente conclusivo é o intervalo da média de mais ou menos dois sigma (95%), enquanto na física de partículas, um novo efeito requer um intervalo de cinco sigmas (99.99994%) para ser considerado uma descoberta.

Exercícios resolvidos

Coelhos na reserva

Em uma reserva de vida selvagem, estima -se que exista uma média de 16.000 coelhos com um desvio padrão de 500 coelhos. Se a distribuição da variável 'número de coelhos na reserva' é desconhecida, é possível.000 e 17.000 coelhos?

O intervalo pode ser apresentado nestes Termos:

15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s

Portanto: [15000, 17000] = [µ - 2 s, µ + 2 s]

Aplicando o teorema de Tchebyshev, há uma probabilidade de pelo menos 0.75 que a população de coelhos da Reserva da Vida Selvagem está entre 15.000 e 17.000 coelhos.

Médias de crianças de um país

O peso médio de um ano -ano é normalmente distribuído com uma média de 10 kg e um desvio padrão de aproximadamente 1 kg para.

a) Estime a porcentagem de crianças de um ano no país com peso médio entre 8 e 12 kg.

8 = 10 - 2 = 10 - 2 (1) = µ - 2 s

12 = 10 + 2 = 10 + 2 (1) = µ + 2 s

Portanto: [8, 12] = [µ - 2s, µ + 2s]

Pode atendê -lo: Teste de Tukey: O que é, em caso de exemplo, exercício resolvido

De acordo com a regra empírica, pode -se afirmar que 68.27% das crianças no país têm entre 8 e 12 kg de peso.

b) Qual é a probabilidade de encontrar um filho de um ano de 7 kg ou menos peso?

7 = 10 - 3 = 10 - 3 (1) = µ - 3 s

Sabe -se que 7 kg de peso representa o valor µ - 3s, bem como se sabe que 99.73% das crianças estão entre 7 e 13 kg de peso. Isso deixa apenas 0.27% do total de crianças para os extremos. Metade deles, 0.135%, tem 7 kg de peso ou menos e a outra metade, 0.135%, tem 11 kg de peso ou mais.

Portanto, pode -se concluir que há uma probabilidade de 0.00135 que uma criança tem 7 kg de peso ou menos.

c) Se a população do país atingir 50 milhões de habitantes e os filhos de 1 ano?

9 = 10 - 1 = µ - s

11 = 10 + 1 = µ + s

Portanto: [9, 11] = [µ - s, µ + s]

De acordo com a regra empírica, 68.27% das crianças de um ano estão no intervalo [µ -s, µ + s]

No país, existem 500.000 crianças de um ano (1% de 50 milhões), então 341350 crianças (68.27% de 500000) têm entre 9 e 11 kg de peso.

Referências

1. Abraira, v. (2002). Desvio padrão e erro padrão. Revista Semergen. Web recuperado.Arquivo.org.
2. Freund, r.; Wilson, w.; Mohr, d. (2010). Métodos estatísticos. Terceira ed. Academic Press-Elsevier Inc.
3. Alicante Server (2017). Regra empírica (termos estatísticos). Glossário recuperado.servidor-aliva.com.
4. Lind, d.; Marchal, w.; Wathen, s. (2012). Estatísticas aplicadas aos negócios e economia. Décima ed. McGraw-Hill/Interamerican do México S. PARA.
5. Salinas, h. (2010). Estatística e Probabilidades. Recuperado da UDA.Cl.
6. Sokal, r.; Rohlf, f. (2009). Introdução à bioestatística. Segunda ed. Dover Publications, Inc.
7. Spiegel, m. (1976). Probabilidade e Estatística. Série Schaum. McGraw-Hill/Interamerican do México S. PARA.
8. Spiegel, m.; Stephens, l. (2008). Estatisticas. Quarto ed. McGraw-Hill/Interamerican do México S. PARA.
9. STAT119 Revisão (2019). Perguntas de regra de solução empírica. Recuperado do STAT119REVIEW.com.
10. (2019). 68-95-99.7 regra. Recuperado de.Wikipedia.org.