Homocedicidade O que é, importância e exemplos

O Homocedicidade Em um modelo estatístico preditivo, ele ocorre se em todos os grupos de dados de uma ou mais observações, a variação do modelo em relação às variáveis ​​explicativas (ou independentes) permanece constante.

Um modelo de regressão pode ser homocedástico ou não, nesse caso, falamos sobre heterocedicidade.

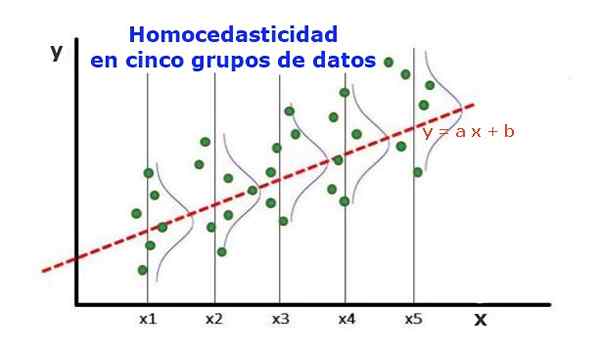
figura 1. Cinco grupos de dados e ajuste de regressão do conjunto. A variação em relação ao valor prevista é a mesma em cada grupo. (UPAV-Library.org)

Um modelo de regressão estatística de várias variáveis ​​independentes é chamado de homocedástico, apenas se a variação do erro variável previsto (ou o desvio padrão da variável dependente) permanecer uniforme para diferentes grupos das variáveis ​​explicativas ou independentes.

Nos cinco grupos de dados da Figura 1, a variação foi calculada em cada grupo, com relação ao valor estimado pela regressão, tornando -se a mesma em cada grupo. Também se supõe que os dados seguem a distribuição normal.

Em um nível gráfico, significa que os pontos são igualmente dispersos ou dispersos em torno do valor previsto pelo ajuste de regressão e que o modelo de regressão tem o mesmo erro e validade para o intervalo da variável explicativa.

[TOC]

Importância da homocedicidade

Para ilustrar a importância da homocedasticidade nas estatísticas preditivas, é necessário contrastar com o fenômeno oposto, heterocedicidade.

Homocedasticidade versus heterocedicidade

No caso da Figura 1, em que há homocedicidade, é cumprido que:

Var ((y1-y1); x1) ≈ var ((y2-y2); x2) ≈ ... var (y4-y4); x4)

Onde var ((yi-ii); xi) representa a variação, o par (xi, yi) representa um fato do Grupo I, enquanto Yi é o valor que prevê a regressão para o valor médio xi do grupo. A variação dos dados do grupo I é calculada da seguinte maneira:

Var ((yi -ii); xi) = ∑j (yij - yi)^2/n

Pelo contrário, quando ocorre heterocedicidade, o modelo de regressão pode não ser válido para toda a região em que foi calculado. A Figura 2 mostra um exemplo desta situação.

Pode atendê -lo: o que são ângulos alternativos internos? (Com exercícios)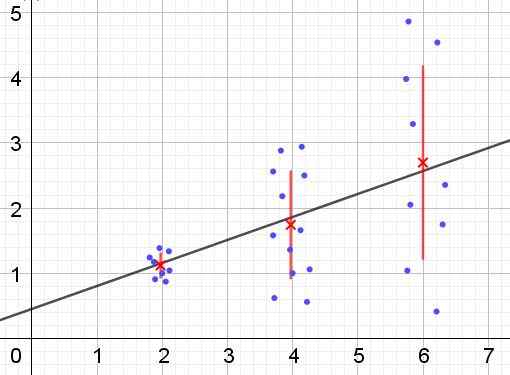 Figura 2. Grupo de dados que têm heterocedicidade. (Elaboração própria)

Na Figura 2, três grupos de dados e o conjunto do conjunto são representados por uma regressão linear. Deve -se notar que os dados no segundo e no terceiro grupo são mais dispersos do que no primeiro grupo. O gráfico da Figura 2 também mostra o valor médio de cada grupo e sua barra de erro ± σ, sendo o desvio padrão σ de cada grupo de dados. Deve -se lembrar que o desvio padrão σ é a raiz quadrada da variação.

Es claro que en el caso de la heterocedasticidad, el error de la estimación por regresión es cambiante en el rango de valores de la variable explicativa o independiente, y en los intervalos donde este error es muy grande, la predicción por regresión es poco confiable o não aplicável.

Em um modelo de regressão, erros ou resíduos (y -y) devem ser distribuídos com igual variação (σ^2) em todo o intervalo de valores variáveis ​​independentes. É por esse motivo que um bom modelo de regressão (linear ou não -linear) deve passar no teste de homocedasticidade. 

Testes de homocedicidade

Os pontos mostrados na Figura 3 correspondem aos dados de um estudo que busca uma relação entre os preços (em dólares) das casas, dependendo do tamanho ou área em metros quadrados.

O primeiro modelo que é ensaiado é o de uma regressão linear. Em primeiro lugar, note -se que o coeficiente de determinação r^2 do ajuste é bastante alto (91%), portanto, pode -se pensar que o ajuste é satisfatório.

No entanto, duas regiões podem ser claramente distinguidas do gráfico de ajuste. Um deles, aquele à direita trancado em um oval, encontra homocedasticidade, enquanto a região da esquerda não tem homocedasticidade.

Pode atendê -lo: grau de um polinômio: como é determinado, exemplos e exercícios

Isso significa que a previsão do modelo de regressão é adequada e confiável na faixa entre 1800 m^2 e 4800 m^2, mas muito inadequada fora desta região. Na área heterocédica, não apenas o erro é muito grande, mas também os dados parecem seguir outra tendência diferente da proposta pelo modelo de regressão linear.

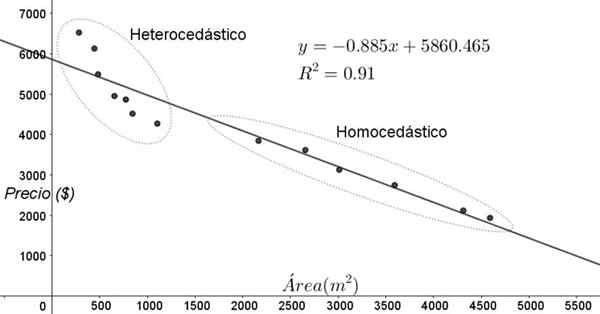Figura 3. Preços da habitação versus área e modelo preditivo por regressão linear, mostrando áreas de homocedasticidade e heterocedicidade. (Elaboração própria)

O gráfico de dispersão de dados é o teste mais simples e visual de sua homocedasticidade, mas às vezes não é tão evidente quanto no exemplo mostrado na Figura 3, é necessário recorrer a gráficos com variáveis ​​auxiliares.

Variáveis ​​padronizadas

Com o objetivo de separar as áreas onde a homocedasticidade é atendida e não, não são introduzidas as variáveis ​​padronizadas ZRES e o ZREDED:

Zres = abs (y - y)/σ

ZPred = y/σ

Deve -se notar que essas variáveis ​​dependem do modelo de regressão aplicado, pois é o valor da previsão de regressão. Abaixo está o gráfico de dispersão Zres vs Zred para o mesmo exemplo:

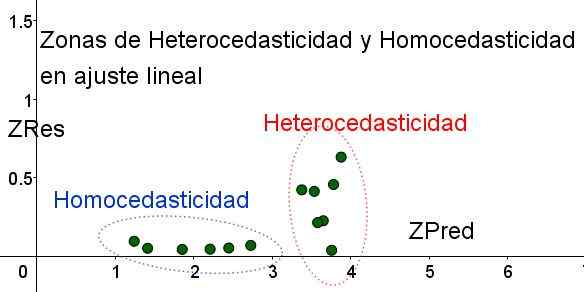Figura 4. Deve -se notar que na zona de homocedasticidade Zres permanece uniforme e pequena na região de previsão (elaboração própria).

No gráfico da Figura 4 com as variáveis ​​padronizadas, a área onde o erro residual é pequeno e o uniforme é claramente separado, com relação ao que não. Na primeira área, a homocedasticidade é cumprida enquanto o erro residual é muito variável e grande.

Um ajuste de regressão é aplicado ao mesmo grupo de dados 3. O resultado é mostrado na figura a seguir:

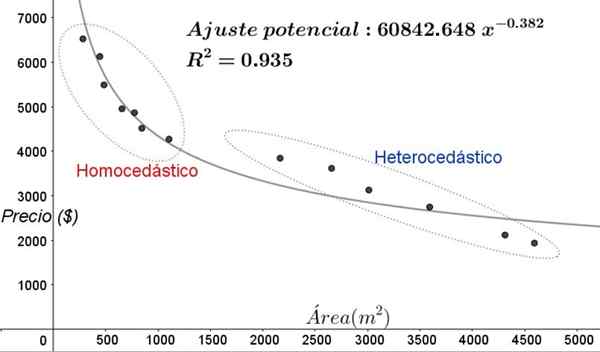Figura 5. Novas áreas de homocedasticidade e heterocedicidade no ajuste de dados com um modelo de regressão não linear. (Elaboração própria).

No gráfico da Figura 5, as áreas homocédicas e heterocedicásticas devem ser claramente notadas. Deve -se notar também que essas áreas foram trocadas em relação àquelas que foram formadas no modelo de ajuste linear.

Pode atendê -lo: tipos de ângulos, características e exemplos

No gráfico da Figura 5, é evidente que, mesmo quando há um coeficiente de determinação do ajuste bastante alto (93,5%), o modelo não é adequado para todo o intervalo da variável explicativa, uma vez que os dados para valores com mais de 2000 M^2 tem heterocedasticidade.

Testes de homocedasticidade não -ográfica

Um dos testes não -ográficos mais utilizados para verificar se a homocedasticidade é ou não atendida ou não Teste de Breusch-Pagan.

Todos os detalhes deste teste não serão dados neste artigo, mas suas características fundamentais e as etapas do mesmo são amplamente descritas:

1. O modelo de regressão é aplicado aos dados n e a variação do mesmo é calculada em relação ao valor estimado pelo modelo σ^2 = ∑j (yj - y)^2/n.
2. Uma nova variável ε = ((yj - y)^2) / (σ^2) é definida
3. O mesmo modelo de regressão é aplicado à nova variável e seus novos parâmetros de regressão são calculados.
4. O valor crítico do qui quadrado (χ^2) é determinado, sendo esta metade da soma dos quadrados novos resíduos na variável ε.
5. Se usa la tabla de la distribución Chi cuadrado considerando en el eje x de la tabla el nivel de significancia (usualmente 5%) y el número de grados de libertad (#de variables de la regresión menos la unidad), para obtener el valor de A tabela.
6. O valor crítico obtido na etapa 3 é comparado com o valor encontrado na tabela (χ^2).
7. Se o valor crítico estiver abaixo do da tabela, você tem a hipótese nula: há homocedicidade
8. Se o valor crítico estiver acima do da tabela, você tem a hipótese alternativa: não há homocedasticidade.

A maioria dos pacotes estatísticos de computador, como: SPSS, Minitab, R, Python Pandas, SAS, Statgraphic e vários outros incorporam o teste de homocedasticidade de Breusch-Pagan. Outro teste para verificar a uniformidade de variância Teste de Levene.

Referências

1. Caixa, caçador e caçador. (1988) Estatísticas para pesquisadores. Eu revertei os editores.
2. Johnston, J (1989). Métodos de Econometria, Vicens -ives Editores.
3. Murillo e González (2000). Manual de economia. Universidade de Las Palmas de Gran Canaria. Recuperado de: ULPGC.é.
4. Wikipedia. Homocedicidade. Recuperado de: é.Wikipedia.com
5. Wikipedia. Homoscedasticidade. Recuperado de: em.Wikipedia.com