Fórmulas de distribuição hipergeométrica, equações, modelo

O Distribuição hipergeométrica É uma função estatística discreta, adequada para calcular a probabilidade em experimentos aleatórios com dois resultados possíveis. A condição necessária para aplicar é que são pequenas populações, nas quais as extrações não são substituídas e as probabilidades não são constantes. 

Portanto, quando um elemento da população é escolhido para saber o resultado (verdadeiro ou falso) de uma certa característica, esse mesmo elemento não pode ser escolhido novamente.

figura 1. Em uma população de parafusos como este, certamente existem espécimes com defeito. Fonte: Pixabay.

Certamente, o próximo elemento escolhido é, portanto, é mais provável que obtenha um resultado verdadeiro, se o elemento anterior tiver um resultado negativo. Isso significa que a probabilidade é variando, na medida em que os elementos da amostra são extraídos.

As principais aplicações da distribuição hipergeométrica são: Controle de qualidade em processos com pouca população e o cálculo de probabilidades em jogos aleatórios.

Quanto à função matemática que define a distribuição hipergeométrica, consiste em três parâmetros, que são:

- Número de elementos da população (n)

- Tamanho da amostra (M) 

- Número de eventos na população completa com um resultado favorável (ou desfavorável) da característica estudada (n).

[TOC]

Fórmulas e equações

A fórmula de distribuição hipergeométrica fornece probabilidade P de que x casos favoráveis ​​de uma certa característica ocorrem. A maneira de escrevê -lo matematicamente, dependendo dos números combinatórios é:

Na expressão anterior N, n e m Eles são parâmetros e x a própria variável. 

-A população total é N.

-Número de resultados positivos de uma certa característica binária em relação à população total é n.

-Número de elementos da amostra é m.

Neste caso, X É uma variável aleatória que obtém valor x e P (x) indica a probabilidade de ocorrência de x casos favoráveis ​​da característica estudada.

Variáveis ​​estatísticas importantes

Outras variáveis ​​estatísticas para a distribuição hipergeométrica são:

- Metade μ = m*n/n

- Variação σ^2 = m*(n/n)*(1-n/n)*(n-m)/(n-1)

- Desvio típico σ que é a raiz quadrada da variação.

Modelo e propriedades 

Para chegar ao modelo de distribuição hipergeométrica, ele é baseado na probabilidade de obter x casos favoráveis ​​em uma amostra de tamanho m. Esta amostra contém elementos que atendem à propriedade em estudo e aos elementos que não.

Vamos lembrar disso n representa o número de casos favoráveis ​​na população total de N Unid. Então a probabilidade seria calculada assim:

Pode servir a você: espaço vetorial: base e dimensão, axiomas, propriedades

P (x) = (# de maneiras de obter x# de maneiras fracassadas)/(# maneiras totais de seleção)

Expressando o acima na forma de números combinatórios, é alcançado o seguinte modelo de distribuição de probabilidades:

Principais propriedades da distribuição hipergeométrica

São as seguintes:

- A amostra deve sempre ser pequena, embora a população seja grande.

- Os elementos da amostra são extraídos de um, sem incorporá -los novamente à população.

- A propriedade a ser estudada é binária, ou seja, só pode levar dois valores: 1 qualquer 0, o bem verdadeiro qualquer falso.

Em cada etapa de extração, a probabilidade muda dependendo dos resultados anteriores.

Abordagem por distribuição binomial

Outra propriedade da distribuição hipergeométrica é que ela pode ser abordada por distribuição binomial, indicada como Bi, Enquanto a população N ser grande e pelo menos 10 vezes maior que a amostra m. Nesse caso, seria assim:

P (n, n, m; x) = bi (m, n/n, x)           

Enquanto n for grande e n> 10m

Exemplos

Exemplo 1

Suponha que uma máquina que produz parafusos e dados acumulados indique que 1% sai com defeitos. Então, em uma caixa de n = 500 parafusos, o número de defeitos será:

N = 500 * 1/100 = 5

Probabilidades através da distribuição hipergeométrica

Suponha que a partir dessa caixa (ou seja, dessa população), coletamos uma amostra de m = 60 parafusos.

A probabilidade de que nenhum parafuso (x = 0) da amostra sai com defeito é de 52,63%. Este resultado é alcançado ao usar a função de distribuição hipergeométrica:

P (500, 5, 60; 0) = 0,5263

A probabilidade de x = 3 parafusos de amostra deixam com defeito é: p (500, 5, 60; 3) = 0,0129.

Por outro lado, a probabilidade de que x = 4 parafusos dos anos sessenta da amostra saia com defeito é: P (500, 5, 60; 4) = 0,0008.

Finalmente, a probabilidade de que x = 5 parafusos nessa amostra saiu com defeito é: p (500, 5, 60; 5) = 0.

Mas se você quiser saber a probabilidade de que, nessa amostra, haja mais de 3 parafusos defeituosos, a probabilidade acumulada deve ser obtida, acrescentando:

P (3)+p (4)+p (5) = 0,0129+0,0008+0 = 0,0137.

Este exemplo é ilustrado na Figura 2, obtido através do uso de Geogebra Uso amplo software livre em escolas, institutos e universidades.

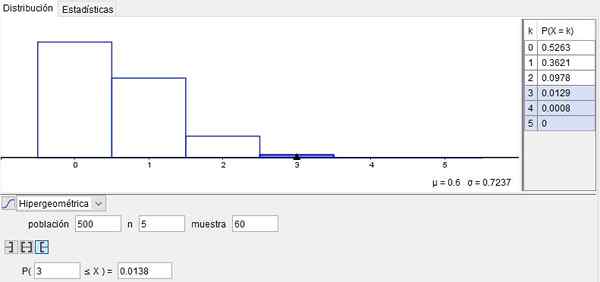Figura 2. Exemplo de distribuição hipergeométrica. Preparado por f. Zapata com geogebra.

Exemplo 2

Um deck de espanhol tem 40 cartas, das quais 10 têm ouro e os 30 restantes não têm. Suponha que 7 cartas sejam extraídas desse baralho, que não retornam ao baralho.

Pode atendê -lo: simetria central: propriedades, exemplos e exercícios

Se x é o número de ouro presente nas 7 cartas extraídas, a probabilidade de X Oros em uma extração de 7 cartões é dada pela distribuição hipergeométrica p (40,10,7; x).

Vejamos isso: para calcular a probabilidade de ter 4 ouro em uma extração de 7 cartões, usamos a fórmula de distribuição hipergeométrica com os seguintes valores:

E o resultado é: 4,57% de probabilidade.

Mas se você quiser saber a probabilidade de obter mais de 4 cartões, teremos que adicionar:

P (4)+p (5)+p (6)+p (7) = 5,20%

Exercícios resolvidos

O seguinte conjunto de exercícios destina -se a ilustrar e assimilar os conceitos que foram apresentados neste artigo. É importante que o leitor tente resolvê -los por conta própria, antes de olhar para a solução.

Exercício 1

Uma fábrica profilática descobriu que de cada 1000 preservativos produzidos por uma determinada máquina, 5 estão com defeito. Para realizar controle de qualidade, 100 preservativos são tomados aleatoriamente e o lote é rejeitado se houver pelo menos um ou mais com defeito. Responder:

a) Que possibilidade deve ser um lote 100 descartado?

b) Este critério de controle de qualidade é eficiente?

Solução

Nesse caso, números combinatórios muito grandes aparecerão. O cálculo é difícil, a menos que um pacote de computador adequado esteja disponível.

Mas como é uma população grande e a amostra é dez vezes menor que a população total, você pode usar a abordagem para a distribuição hipergeométrica devido à distribuição binomial:

P (1000,5,100; x) = bi (100, 5/1000, x) = bi (100, 0.005, x) = c (100, x)*0.005^x (1-0.005)^(100-X)

Na expressão anterior C (100, x) É um número combinatório. Então, a probabilidade de Haya mais de um defeituoso será calculada da seguinte forma:

P (x> = 1) = 1 - bi (0) = 1-.6058 = 0.3942

É uma excelente abordagem, se comparada ao valor obtido ao aplicar a distribuição hipergeométrica: 0.4102

Pode -se dizer que, 40% de probabilidade de muitos 100 profiláticos devem ser descartados, o que não é muito eficiente.

Mas, sendo um pouco menos exigente no processo de controle de qualidade e descarte.

Exercício 2

Uma máquina de taco de plástico funciona de tal maneira que de cada 10 peças, uma é deformada. Em uma amostra de 5 peças, essa possibilidade deve estar com defeito.

Solução

População: n = 10

Pode servir a você: identidades pitagóricas: demonstração, exemplo, exercícios

Número N Defeito para cada n: n = 1

Tamanho da amostra: M = 5

P (10, 1, 5; 1) = c (1,1)*C (9,4)/c (10,5) = 1*126/252 = 0.5

Portanto, há uma probabilidade de 50% de que em uma amostra de 5, um taco sai deformado.

Exercício 3

Em uma reunião de jovens escolas secundárias, existem 7 senhoras e 6 cavalheiros. Entre as meninas, 4 estudam humanidades e 3 ciências. No grupo de meninos, 1 estuda humanidades e 5 ciências. Calcule o seguinte:

a) Escolhendo aleatoriamente três meninas: qual é a probabilidade de que todos estudem humanidades?.

b) Se três participantes forem escolhidos aleatoriamente para a reunião de amigos: o que são três deles, independentemente do sexo, estudar as três ou as humanidades também todos os três?.

c) Agora selecione dois amigos aleatórios e ligue x para a variável aleatória "Número daqueles que estudam humanidades". Entre os dois escolhidos, determine o valor médio ou esperado de x e a variação σ^2.

Solução para 

A população é o número total de meninas: n = 7. Aqueles que estudam humanidades são n = 4, do total. A amostra aleatória de meninas será m = 3.

Nesse caso, a probabilidade de que os três sejam humanidades sejam dadas pela função hipergeométrica:

P (n = 7, n = 4, m = 3, x = 3) = c (4, 3) c (3, 0) / c (7, 3) = 0.1143

Então há 11.4% de probabilidade de que três chicas aleatórias estudem humanidades.

Solução b

Os valores a serem usados ​​são:

-População: n = 14

-Quantidade que estuda as cartas é: n = 6 e o

-Tamanho da amostra: M = 3.

-Número de amigos que estudam humanidades: x

De acordo com isso, x = 3 significa que as três humanidades do estudo, mas x = 0 significa que ninguém estuda humanidades. A probabilidade de que os três estudos sejam dados pela soma:

P (14, 6, 3, x = 0) + p (14, 6, 3, x = 3) = 0.0560 + 0.1539 = 0.2099

Em seguida, temos uma probabilidade de 21% de que três participantes da reunião, escolhidos aleatoriamente.

Solução c

Aqui temos os seguintes valores:

N = 14 população total de amigos, n = 6 número total na população que estuda humanidades, o tamanho da amostra é m = 2.

A esperança é:

E (x) = m * (n/n) = 2 * (6/14) = 0.8572

E a variação:

σ (x)^2 =  M*(n/n)*(1-n/n)*(n-m)/(n-1) = 2*(6/14)*(1-6/14)*(14-2)/(14 -1) =

= 2*(6/14)*(1-6/14)*(14-2)/(14-1) = 2*(3/7)*(1-3/7)*(12) (13)  = 0.4521

Referências

1. Distribuições de probabilidade discreta. Recuperado de: biploot.USAL.é
2. Estatística e probabilidade. Distribuição hipergeométrica. Recuperado de: Projectodescartes.org
3. CDPYE-AGR. Distribuição hipergeométrica. Recuperado de: UGR.é
4. Geogebra. Geogebra clássico, cálculo de probabilidade. Recuperado da geogebra.org
5. Probate fácil. Exercícios de distribuição hipergeométrica resolvidos. Recuperado de: probafacil.com
6. Minitab. Distribuição hipergeométrica. Recuperado de: suporte.Minitab.com
7. Universidade de Vigo. Principais distribuições discretas. Recuperado de: Anapg.sites.Uvigo.é
8. Vitutor. Estatísticas e combinatórios. Recuperado de: Vitutor.líquido
9. Weisstein, Eric W. Distribuição hipergeométrica. Recuperado de: Mathworld.Volfrâmio.com
10. Wikipedia. Distribuição hipergeométrica. Recuperado de: é.Wikipedia.com