Volume específico

Explicamos qual é o volume específico, sua fórmula, unidades, como ela é calculada e damos vários exemplos de cálculo

Qual é o volume específico?

Ele Volume específico (Representado com o símbolo ν, letra grega nu) é uma propriedade intensiva do assunto que mede o volume ocupado por unidade de massa de um corpo. Corresponde à relação entre volume e massa, por isso representa o inverso da densidade. Isso significa que, quanto mais denso um corpo, menor seu volume específico e vice -versa.

Conhecer o volume específico de uma substância é importante em aplicações nas quais o volume disponível é limitado. Por exemplo, selecionando o combustível para um foguete espacial, o ideal é que o combustível tem como um volume possível específico, pois, caso contrário, terá muito espaço, o que exigirá um foguete muito grande e caro.

Volumes específicos também são de grande importância no campo da termodinâmica, pois permitem simplesmente calcular volumes molares de diferentes substâncias de sua massa molar ou determinar o volume total de uma amostra de sua massa.

Finalmente, mudanças específicas de volume também permitem mudanças de fase, como fusão e ebulição, entre outros.

Fórmula de volume específico

A equação a seguir corresponde à definição matemática do volume específico:

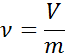
Onde V é o volume de um corpo ou substância, m é sua massa e ν é o volume específico. No entanto, também pode ser calculado a partir da densidade, pois, como mencionado acima, o volume específico é o inverso da densidade:

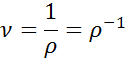
Onde ρ representa densidade.

Unidades de volume específicas

As unidades de volume específicas são unidades de volume em unidades de massa. Como de costume, essas magnitudes podem ser expressas em diferentes sistemas de unidades; portanto, o volume específico também pode ser expresso em diferentes unidades.

Pode servir a você: eletrofilo: reações, exemplos, eletrofilidade

A tabela a seguir mostra as unidades de volume específicas nos sistemas de unidades mais importantes:

Sistema unitário	Unidades de volume específicas
S.Yo.	m3/kg
Mks	m3/kg
CGS	cm3/g
Sistema Anglo -Saxon	Pie3/lb
Outras unidades	ml/g ou cm3/g

Cálculo de volume específico

Para sólidos regulares

No caso de sólidos regulares, a maneira mais fácil de determinar o volume específico é determinar o volume das dimensões do sólido e depois dividir entre a massa.

Para determinar o volume do sólido, a fórmula de volume correspondente à forma particular do sólido (esfera, cone, cilindro, etc.).

Exemplo 1: barra cilíndrica

Você tem uma barra cilíndrica sólida de 2,54 cm de espessura, 10 cm de comprimento e uma massa de 1,50 kg. Determinar o volume específico do material nas unidades do S.Yo.

• Solução: Como sabemos que é um cilindro, então devemos usar a fórmula de volume de um cilindro e depois aplicar a fórmula de volume específica. Ambas as equações podem ser combinadas em uma, como mostrado abaixo:

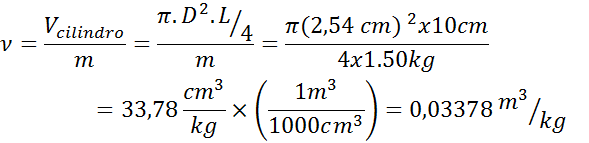
Exemplo 2: Esfera de vidro

Um mármore de vidro de 1 cm de diâmetro é pesado em um equilíbrio. Esta leitura 2,50 g. Determinar o volume específico de vidro.

• Solução: Do diâmetro, sabe -se que o raio da esfera é de 0,50 cm. Com este raio e usando a fórmula de volume de uma esfera, podemos determinar o volume do mármore. Então usamos a fórmula de volume específica. Você também pode combinar as duas equações em uma:

Pode servir a você: Trioxido de Arsênico (AS2O3)

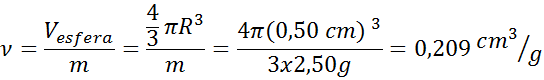
Para sólidos amorfos

No caso de sólidos amorfos, não é possível determinar seu volume por meio de fórmulas, pois não são sólidos regulares. Uma solução possível é determinar o volume do corpo por meio do volume que desloca ao mergulhar em água ou outro líquido:

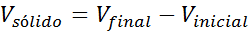
Exemplo 3: Um meteorito

Um meteorito foi encontrado muito estranhamente. Primeiro, foi pesado, após o qual uma massa de 185,3 g foi obtida. Em seguida, foi introduzido em um cilindro graduado que continha 50,0 ml de água. Depois de submergir o meteorito, o nível da água aumentou para 73,5 ml. Determine o volume específico do meteorito.

• Solução: Como mencionado acima, o volume do meteorito é determinado pelo deslocamento do líquido. A diferença entre os volumes de água no cilindro graduado antes e depois de submergir o meteorito fornece o volume do mesmo. Em seguida, a fórmula de volume específica é aplicada:

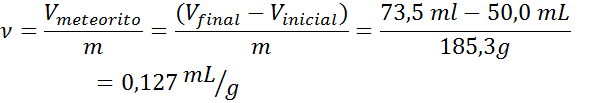
Exemplo 4: uma rocha

Perto do local onde foi encontrado o meteorito do exemplo anterior, outra rocha foi encontrada com aparência semelhante. Isso também foi pesado, obtendo uma massa de 125 g e imersa na água, onde deslocou 15,90 ml do líquido. Determinar se é ou não um fragmento de meteorita.

• Solução: O volume específico é uma propriedade intensiva; portanto, se a rocha for feita do mesmo material que o meteorito, deve ter o mesmo volume específico.

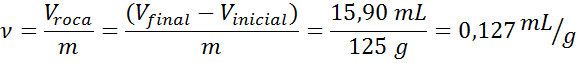
Como pode ser visto, o volume específico da rocha é idêntico ao do meteorito, por isso é possível que a rocha seja um fragmento dela.

Pode atendê -lo: nitrobenzeno (c6h5n2): estrutura, propriedades, usos, riscos

Líquido

Calcule o volume específico de um líquido é feito da mesma maneira que foi mostrado nos exemplos anteriores. O volume pode ser facilmente medido usando material volumétrico. Você também pode calcular o volume específico a partir da densidade do líquido, como mostrado no exemplo a seguir.

Exemplo 5: volume específico de álcool desnaturado

Determine o volume específico de álcool desnaturado, sabendo que tem uma densidade de 0,876 g/ml.

• Solução: Sabemos que o volume específico é o inverso da densidade, então:

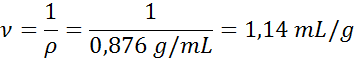
Para gases

Em vista do fato de que a maioria dos gases está em conformidade com a lei ideal para gases relativamente bem, essa equação pode ser usada para determinar o valor de volume específico de um gás. Após reordenar esta equação, o seguinte relacionamento é obtido:

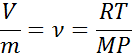
onde r, t, m e p são a constante de gases ideais, temperatura, massa molar de gás e pressão, respectivamente.

Exemplo 6: volume de ar específico

Calcule o volume específico de uma amostra de ar encontrada em 2 atm de pressão e 350 ° C, sabendo que a massa molar média do ar é de 28,96 g/mol.

• Solução: Para usar esta equação, é necessário transformar a temperatura para Kelvin, adicionando 273 na temperatura em graus Celsius: t = 350+273 = 623 K. Agora podemos aplicar a equação anterior, usando o valor da constante r = 0,08206 ATL.L/mol.K: