Cálculo normal e vetor de exemplo

Ele Vetor normal É aquele que define a direção perpendicular a uma entidade geométrica em consideração, que pode ser para uma curva, um plano ou uma superfície, por exemplo.

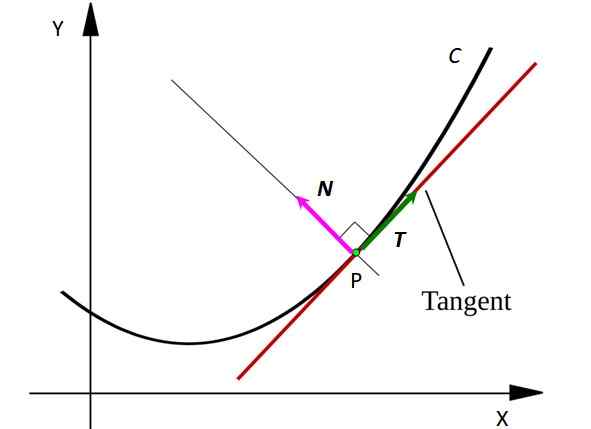
É um conceito muito útil no posicionamento de uma partícula móvel ou alguma superfície no espaço. No gráfico seguinte, é possível ver como o vetor normal é para uma curva arbitrária C:

figura 1. Uma curva C com o vetor normal à curva no ponto P. Fonte: SVJO [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

Considere um ponto P na curva c. O ponto pode representar uma partícula móvel que se move após uma estrada em forma de C. A linha tangente à curva no ponto P aparece desenhada em vermelho.

Observe que o vetor T É tangente para C em cada ponto, enquanto o vetor N é perpendicular a T e aponta para o centro de uma circunferência imaginária cujo arco é um segmento de C. Os vetores são indicados em letra ousada em texto impresso, para distingui -los de outras magnitudes não -vetoriais.

O vetor T Sempre indica onde a partícula se move, portanto indica a velocidade do mesmo. Em vez disso, o vetor N Sempre aponte na direção em que a partícula está girando, dessa maneira indica a concavidade da curva C.

[TOC]

Como levar o vetor normal a um avião?

O vetor normal não é necessariamente um vetor de unidade, ou seja, um vetor cujo módulo é 1, mas se sim, é chamado vetor de unidade normal.

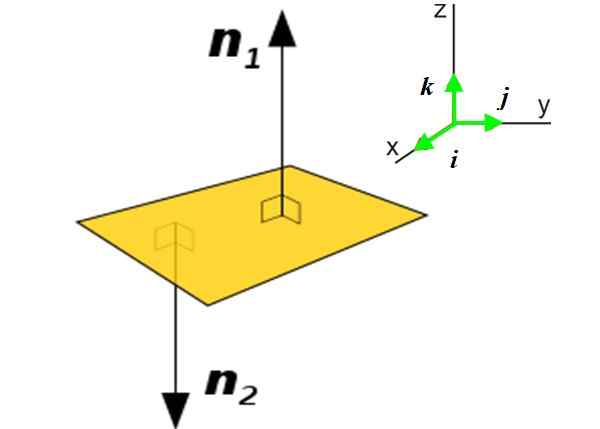Figura 2. À esquerda, um avião P e os dois vetores normais para o referido avião. À direita, os vetores da unidade nas três direções que determinam o espaço. Fonte: Wikimedia Commons. Veja a página para o autor [domínio público]

Em inúmeras aplicações, é necessário conhecer o vetor normal em um avião em vez de uma curva. Este vetor torna conhecida a orientação do referido plano no espaço. Por exemplo, considere o avião P (amarelo) da figura:

Pode atendê -lo: gemine: origens, características e como observá -las

Existem dois vetores normais nesse avião: n₁ e n₂. O uso de um ou outro dependerá do contexto em que o referido plano é encontrado. A obtenção do vetor normal a um avião é muito simples se a equação dela for conhecida:

AX + por + CZ + D = 0, com para, b, c e d numeros reais.

Bem, um vetor plano normal é dado por:

N = a Yo + b J + c k

Aqui o vetor N é expresso em termos de vetores unitários e perpendicular um ao outro Yo, J e k, dirigido ao longo das três direções que determinam o espaço X e z, Veja Figura 2 Right.

O vetor normal do produto vetorial

Um procedimento muito simples para encontrar o vetor normal faz uso das propriedades do produto vetorial entre dois vetores.

Como se sabe, três pontos diferentes e não colineal um com o outro, determine um plano p. Agora, é possível obter dois vetores ou e v que pertencem ao referido avião tendo esses três pontos.

Uma vez que os vetores são, o Produto vetorial ou x v É uma operação cujo resultado é um vetor, que tem a propriedade de ser perpendicular ao plano determinado por ou e v.

Conhecido este vetor, é denotado como N, E, a partir dele, será possível determinar a equação do avião graças à equação indicada na seção anterior:

N = ou x v

A figura a seguir ilustra o procedimento descrito:

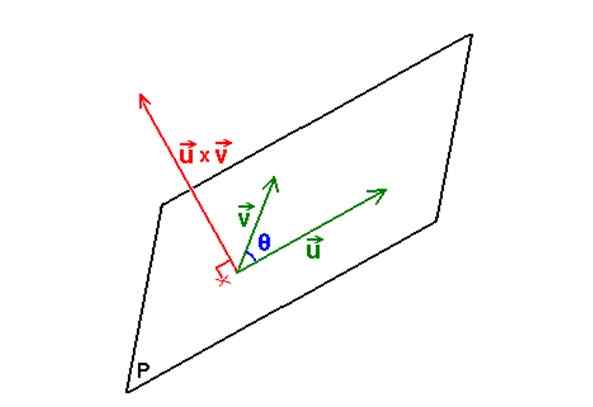Figura 3. Com dois vetores e seu vetor ou produto cruzado, a equação do plano contendo os dois vetores é determinada. Fonte: Wikimedia Commons. Nenhum autor legível por máquina fornecido. M.Romero Schmidtke assumiu (com base em reivindicações de direitos autorais). [Domínio público]

Exemplo

Encontre a equação do plano determinado pelos pontos A (2,1,3); B (0,1,1); C (4,2,1).

Pode atendê -lo: equação de continuidade

Solução

Este exercício ilustra o procedimento descrito acima. Por ter 3 pontos, um deles é escolhido como uma origem comum de dois vetores que pertencem ao plano definido por esses pontos. Por exemplo, o ponto A é definido como origem e vetores são construídos Ab e AC.

O vetor Ab É o vetor cuja origem é o ponto A e cujo fim é o ponto B. Coordenadas do vetor Ab As coordenadas de B das coordenadas de A:

Ab = (0-2) Yo + (1-1) J + (1-3) k = -2Yo + 0J -2 k

Prosseguir da mesma maneira para encontrar o vetor AC:

AC = (4-2) Yo + (2-1) J + (1-3) k = 2Yo + J -2 k

Cálculo do produto vetorial Ab x ac

Existem vários procedimentos para encontrar o produto vetorial entre dois vetores. Neste exemplo, é usado um procedimento mnemônico que utiliza a figura a seguir para encontrar produtos vetoriais entre os vetores da unidade Yo, J e K:

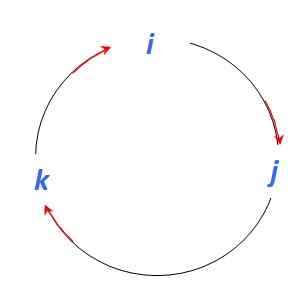Figura 4. Gráfico para determinar o produto vetorial entre os vetores da unidade. Fonte: Self feito.

Para começar, é bom lembrar que os produtos vetoriais entre vetores paralelos são nulos, portanto:

Yo x Yo = 0; J x J = 0; k x k = 0

E como o produto vetorial é outro vetor perpendicular aos vetores participantes, movendo -se na direção da seta vermelha que você possui:

Yo x J = k ; J x k = Yo; k x Yo = J

Se você precisar se mover ao contrário da seta, um sinal (-) será adicionado:

J x Yo = - k; k x J = -Yo; Yo x k = -J

No total, é possível fazer 9 produtos vetoriais com os vetores da unidade Yo, J e k, dos quais 3 serão nulos.

Ab x AC = (-2Yo + 0J -2 k) X (2Yo + J -2 k) = -4 (Yo x Yo) -2 (Yo x J) +4 (Yo x k) +0 (J x Yo) + 0 (J x J) - 0 (J x k) - 4 (k x Yo) -2 (k x J) + 4 (k x k) = -2k-4J-4J+2Yo = 2Yo -8J-2k

Equação plana

O vetor n foi determinado pelo produto vetorial calculado anteriormente:

Pode atendê -lo: movimento pendular

N = 2Yo -8J-2k

Portanto, a = 2, b = -8, c = -2, o plano procurado é:

Ax + por + Cz + D = 0 → 2x-8y-2z + D = 0

O valor de d. Isso é fácil se os valores de qualquer um dos pontos a, b ou c dos quais estão disponíveis forem substituídos na equação plana. Escolhendo C, por exemplo:

x = 4; y = 2; Z = 1

É sobrou:

2.4 - 8.2 - 2.1 + d = 0

-10 + d = 0

D = 10

Em suma, o avião desejado é:

2x-8y-2z +10 = 0

O leitor inquisitivo pode perguntar se o mesmo resultado teria sido obtido se, em vez de fazer Ab x AC Teria sido escolhido AC x Ab. A resposta é sim, o plano determinado por esses três pontos é único e tem dois vetores normais, como mostrado na Figura 2.

Quanto ao ponto selecionado como a origem dos vetores, também não há inconveniência na escolha de qualquer um dos outros dois.

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB). 31-62.
2. Encontrando o normal para um avião. Recuperado de: web.MA.Utexas.Edu.
3. Larson, r. (1986). Cálculo e geometria analítica. Mc Graw Hill. 616 - 647.
4. Linhas e planos em R 3. Recuperado de: matemática.Harvard.Edu.
5. Vetor normal. Recuperado do Mathworld.Volfrâmio.com.