Físico

Equação do diretor vetorial da linha, exercícios resolvidos

Equação do diretor vetorial da linha, exercícios resolvidos

É entendido por Diretor Vector aquele que define a direção de uma linha, seja no avião ou no espaço. Portanto, um vetor paralelo à linha pode ser considerado como diretor do mesmo.

Isso é possível graças a um axioma da geometria euclidiana que diz que dois pontos definem uma linha. Em seguida, o segmento orientado que forma esses dois pontos também define um diretor vetorial dessa linha.

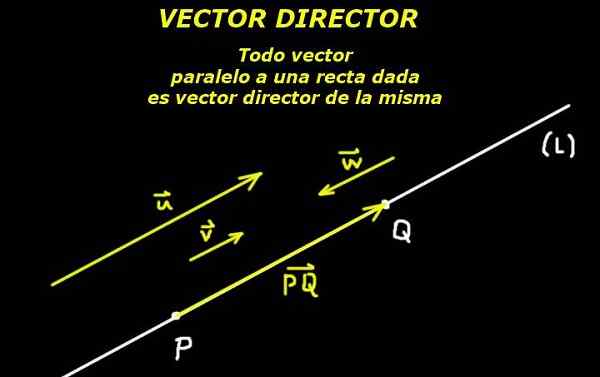figura 1. Diretor vetorial de uma linha. (Elaboração própria)

Dado um ponto P pertencente à linha (EU) e dado um vetor de diretor ou Dessa linha, a linha é completamente determinada.

[TOC]

Equação da linha e diretor diretor

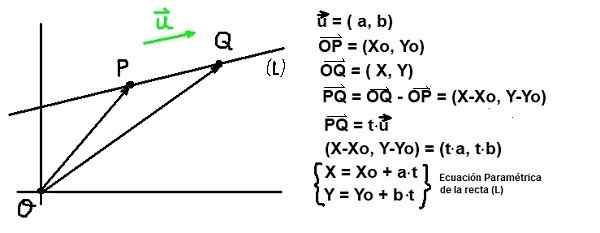
Figura 2. Equação da linha e diretor diretor. (Elaboração própria)

Dado um ponto P de coordenadas P: (XO, eu) e um vetor ou Diretor de uma linha (EU), Todos os pontos Q de coordenadas Q: (x, y) deve cumprir que o vetor Pq ser paralelo a você. Esta última condição é garantida se Pq É proporcional a ou:

Pq = T⋅ou

Na expressão anterior t É um parâmetro que pertence a números reais.

Se os componentes cartesianos de Pq e de ou A equação anterior é escrita da seguinte forma:

(X-xo, y-yo) = t⋅ (a, b)

Se os componentes da igualdade vetorial forem iguais ao seguinte par de equações:

X - XO = a⋅t      e   E - eu = b⋅t 

Equação paramétrica da linha

As coordenadas X e E de um ponto pertencente à linha (EU) isso passa por um ponto de coordenada (Xo, eu) E é paralelo a Diretor Vector ou= (a, b) Eles são determinados atribuindo valores reais ao parâmetro variável t:

X = xo + a⋅t; Y = me + b⋅t

Exemplo 1

Para ilustrar o significado da equação paramétrica da linha, tomamos como diretor vetor

Pode atendê -lo: Óptica ondulada

ou = (a, b) = (2, -1) 

e como um ponto conhecido da linha o ponto 

P = (XO, ME) = (1, 5). 

A equação paramétrica da linha é:

X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞

Para ilustrar o significado desta equação, a Figura 3 mostra, onde o parâmetro t está mudando o valor e o ponto Q  de coordenadas (X, y) Tire posições diferentes na linha.

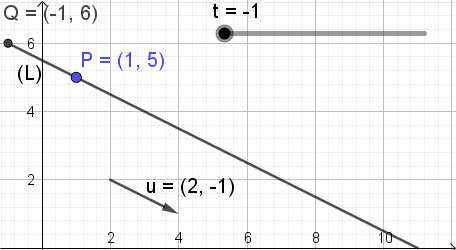Figura 3. Pq = t u. (Elaboração própria)

A linha em forma de vetor

Dado um ponto P da linha e seu diretor ou a equação da linha podem ser escritos em um formulário vetorial:

Oq = Op + λ⋅ou 

Na equação anterior que é qualquer ponto, mas pertencente à linha e λ Um número real.

A equação vetorial da linha é aplicável a qualquer número de dimensões, mesmo um hipereret pode ser definido.

No caso tridimensional para um vetor de diretor ou= (a, b, c) e um ponto P = (xo, eu, zo), As coordenadas de um ponto genérico Q = (x, y, z) Pertencente à linha é:

(X e z) = (Xo, i, zo) + λ⋅ (a, b, c)

Exemplo 2

Considere novamente a linha que tem como diretor  

ou = (a, b) = (2, -1) 

e como um ponto conhecido da linha o ponto 

P = (XO, ME) = (1, 5). 

A equação vetorial desta linha é:

(X, y) = (1, 5) + λ⋅ (2, -1) 

Forma contínua da linha e o vetor do diretor

A partir da forma paramétrica, limpando e combinando o parâmetro λ você tem:

(X-xo)/a = (y-yo)/b = (z-zo)/c

Esta é a forma simétrica da equação de linha. Eu sinto isso para, b e c Eles são os componentes do vetor do diretor.

Exemplo 3

Considere a linha que tem como diretor diretor  

ou = (a, b) = (2, -1) 

e como um ponto conhecido da linha o ponto 

Pode atendê -lo: qual é a eletricidade? (Com experimento)

P = (XO, ME) = (1, 5). Encontre sua forma simétrica.

A forma simétrica ou contínua é da linha é:

(X - 1)/2 = (y - 5)/( - 1)

Forma geral da equação de linha

É conhecido como a forma geral da linha no plano XY para a equação que a estrutura a seguir possui:

A⋅x + b⋅y = c

A expressão da forma simétrica pode ser reescrita para ter a forma geral:

B⋅x - a⋅y = b⋅xo - a⋅o

Comparando com a forma geral da linha permanece: 

A = b, b = -a e c = B⋅xo - a⋅o 

Exemplo 3

Encontre a forma geral da linha cujo diretor é u = (2, -1)

 E o que passa pelo ponto P = (1, 5).

Para encontrar a forma geral, podemos usar as fórmulas dadas, no entanto, um caminho alternativo será escolhido.

Começamos encontrando o vetor W duplo do vetor u, definido como o vetor que é obtido trocando os componentes de u e multiplicando por -1 o segundo:

C= (-1, -2)

O vetor duplo C corresponde a uma rotação em 90 ° no cronograma do diretor v.

Nós multiplicamos escalando C com (X, y) e com (Xo, eu) E nós combinamos:

(-1, -2) • (x, y) = (-1, -2) • (1, 5)

-X -2y = -1 -2⋅5 = -11

Finalmente restante:

X + 2y = 11

Forma padrão da equação de linha

É conhecido como forma padrão da linha no plano XY, aquele que possui a seguinte estrutura:

Y = m⋅x + d

onde m representa a inclinação e a interceptação com o eixo e.

Dado o diretor u = (a, b) vetor, a inclinação m é b/a.

E D é obtido substituindo X e Y pelo ponto conhecido XO, eu:

I = (b/a) xo + d.

Em suma, m = b/a y d = me -(b/a) xo

Observe que a inclinação m é o quociente entre o componente e do diretor e o componente x do mesmo.

Pode servir a você: Equilíbrio rotacional: fórmulas e equações, exemplos, exercícios

Exemplo 4

Encontre a forma padrão da linha cujo diretor é u = (2, -1) 

E o que passa pelo ponto P = (1, 5).

M = -½ e d = 5 -( -½) 1 = 11/2

Y = (-1/2) x + 11/2

Exercícios resolvidos

-Exercício 1

Encontre um diretor vetorial da linha (L), que é a interseção do plano (π): x - y + z = 3 e o plano (ω): 2x + y = 1.

Em seguida, escreva a forma contínua da linha da linha (L).

Solução

Da equação plana (ω) depuração y: y = 1 -2x

Então substituímos na equação plana (π):

X - (1 - 2x) + z = 3 ⇒ 3x + z = 4 ⇒ z = 4 - 3x

Em seguida, parametrizamos x, escolhemos a parametrização x = λ

Isso significa que a linha tem uma equação vetorial dada por:

(X, y, z) = (λ, 1 - 2λ, 4 - 3λ)

que pode ser reescrito como:

(X, y, z) = (0, 1, 4) + λ (1, -2, -3)

Com o que está claro que o vetor ou = (1, -2, -3) é um vetor de gerenciamento direto (L).

A forma contínua da linha (l) é:

(X - 0)/1 = (y - 1)/( - 2) = (z - 4)/( - 3)

-Exercício 2

Dado o avião 5x + para Y + 4z = 5 

e a linha cuja equação é x/1 = (y-2)/3 = (z -2)/(-2)

Determinar o valor de para para que o avião e a linha sejam paralelos.

Solução 2

O vetor n = (5, a, 4) é um vetor normal para o plano.

O vetor ou = (1, 3, -2) é um gerente direto.

Se a linha estiver paralela ao avião, então n • v = 0.

(5, para, 4)•(1, 3, -2) = 5 +3para -8 = 0 ⇒ para= 1.

Referências

  1. Fleming, w., & Varberg, D. E. (1989). Matemática do Pré -Eleno. Prentice Hall Ptr.
  2. Kolman, b. (2006). Álgebra Linear. Pearson Education.
  3. Leal, j. M., & Viloria, n. G. (2005). Geometria analítica plana. Mérida - Venezuela: editorial venezuelano C. PARA.
  4. Navarro, Rocio. Os vetores. Recuperado de: livros.Google.co.ir.
  5. Pérez, c. D. (2006). Pré -qualculus. Pearson Education.
  6. PreNowitz, w. 2012. Conceitos básicos de geometria. Rowman & Littlefield.
  7. Sullivan, m. (1997). Pré -qualculus. Pearson Education.