Trajetória e deslocamento

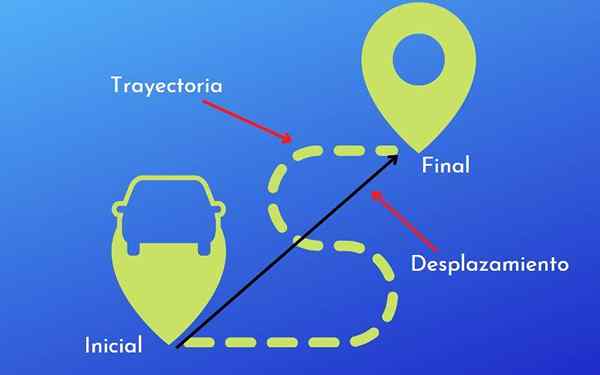
Diferença entre trajetória e deslocamento. Com licença

O Diferença entre trajetória e deslocamento é que o último é a distância e a direção percorrida por um objeto, enquanto a trajetória é a rota ou a forma adotada pelo movimento desse objeto.

No entanto, para ver mais claramente as diferenças entre deslocamento e trajetória, é melhor explicar através de exemplos que permitem uma maior compreensão de ambos os termos.

Deslocamento

É entendido como a distância e a direção percorridas por um objeto, levando em consideração sua posição inicial e sua posição final, sempre em uma linha reta. Para seu cálculo, porque é uma magnitude vetorial, as medidas de comprimento conhecidas como centímetros, medidores ou quilômetros são usadas.

A fórmula para calcular o deslocamento é definida da seguinte forma:

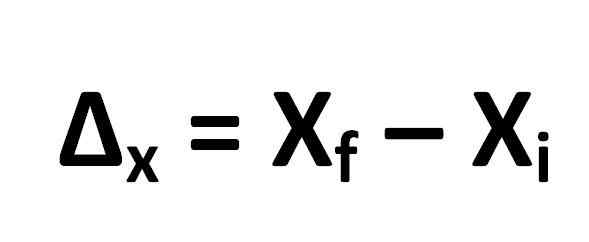
Do qual se segue:

- Δ_x = deslocamento

- X_F = posição final do objeto

- X_Yo = posição inicial do objeto

Exemplo de deslocamento

1. Se um grupo de crianças estiver no início de uma rota, cuja posição inicial é de 50 m, movendo -se em linha reta, determinando o deslocamento em cada um dos pontos x_F. 

- X_F = 120 m

- X_F = 90 m

- X_F = 60 m

- X_F = 40 m

2. Os dados do problema são extraídos substituindo os valores de x₂ e x₁ Na fórmula de deslocamento:

- Δ_x = ?

- X_Yo = 50 m

- Δ_x = X_F - X_Yo

- Δ_x = 120 m - 50 m = 70 m

3. Nesta primeira abordagem, dizemos que δ_x É igual a 120 m, que corresponde ao primeiro valor que encontramos de x_F, menos 50 m, que é o valor de x_Yo, Isso resulta em 70 m, ou seja, ao atingir 120 m viajou, o deslocamento foi de 70 m para a direita.

Pode atendê -lo: ramo de laboratório

4. Passamos a resolver da mesma maneira para os valores de B, C e D

- Δ_x = 90 m - 50 m = 40 m

- Δ_x = 60 m - 50 m = 10 m

- Δ_x = 40 m - 50 m = - 10 m

Nesse caso, o deslocamento nos deu negativo, isso significa que a posição final está na direção oposta da posição inicial.

Trajetória

É a rota ou linha determinada por um objeto durante seu movimento e sua avaliação no sistema internacional, geralmente adota formas geométricas, como linha, parábola, círculo ou elipse.

É identificado através de uma linha imaginária e por ser uma quantidade escalar, é medida em metros.

Deve -se notar que, para calcular a trajetória, devemos saber se o corpo está em repouso ou em movimento, ou seja, é submetido ao sistema de referência que selecionamos.

A equação para calcular a trajetória de um objeto no sistema internacional é dada por:

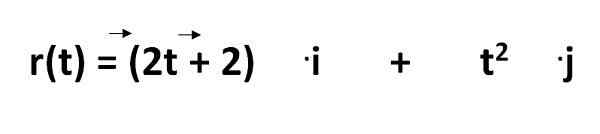
Dos quais temos que:

- R (t) = é a equação de trajetória

- 2T - 2 e T² = representar as coordenadas em função do tempo

-  ^.eu e ^.J = são os vetores da unidade

Para entender o cálculo da trajetória viajada por um objeto, desenvolveremos o seguinte exemplo:

Calcule a equação das trajetórias dos seguintes vetores de posição:

- R (t) = (2T + 7) ^.i + t^{2 .}J

- R (t) = (t - 2) ^.R&D 2T ^.J

Primeira etapa: como uma equação de trajetória é uma função de x, pois isso define os valores de x e y, respectivamente, em cada um dos vetores levantados:

1. Resolva o vetor de primeira posição:

- R (t) = (2T + 7) ^.i + t^{2 .}J

2. Ty = f (x), onde x é dado pelo conteúdo do vetor de unidade ^.Eu e é dado pelo conteúdo do vetor da unidade ^.J:

Pode atendê -lo: ad hoc: origem do termo, significados e exemplos de uso

- X = 2t + 7

- Y = t²

3. y = f (x), isto é, o tempo não faz parte da expressão; portanto, devemos esclarecer, temos:

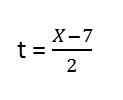
4. Substituímos a folga em e. Fica:

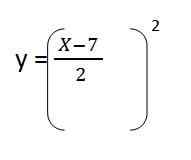
5. Resolvamos o conteúdo dos parênteses e temos a equação da trajetória resultante para o primeiro vetor de unidade:

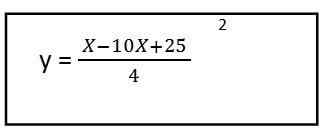
Como podemos ver, resultou em uma equação de segundo grau, isso significa que a trajetória é para a forma de uma parábola.

Segunda etapa: prosseguimos da mesma maneira para o cálculo da trajetória do vetor da segunda unidade:

1. R (t) = (t - 2) ^.R&D 2T ^.J

- X = t - 2

- Y = 2t

2. Seguindo as etapas que vimos anteriormente y = f (x), devemos limpar o tempo porque não faz parte da expressão, temos:

- t = x + 2

3. Substituímos a folga e, permanecendo:

- y = 2 (x + 2)

4. Resolvendo os parênteses, temos a equação da trajetória resultante para o vetor da segunda unidade:

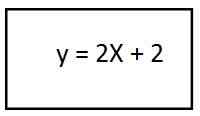
Neste procedimento, resultamos em uma linha, o que nos diz que a trajetória tem uma forma retilínea.

Entendeu os conceitos de deslocamento e trajetória, podemos deduzir o restante das diferenças que existem entre os dois termos.

Mais diferenças entre deslocamento e trajetória

Deslocamento

- É a distância e a direção percorrida por um objeto levando em consideração sua posição inicial e sua posição final.

- Sempre acontece em uma linha reta.

- É reconhecido com uma flecha.

- Use medidas de comprimento (centímetro, medidor, quilômetro).

- É uma quantidade de vetor.

- Leve em consideração a direção percorrida (direita ou esquerda)

- Não considera o tempo gasto durante o passeio.

Pode atendê -lo: condensação: conceito, processo, exemplos

- Não depende de um sistema de referência.

- Quando o ponto de partida é o mesmo ponto de partida, o deslocamento é zero.

- O módulo deve coincidir com o espaço a ser excitado enquanto a trajetória é uma linha reta e não há mudanças no sentido a seguir.

- O módulo tende a aumentar ou diminuir à medida que o movimento ocorre, levando em consideração a trajetória.

Trajetória

É a rota ou linha determinada por um objeto durante seu movimento. Adote formas geométricas (retas, parabólicas, circulares ou elípticas).

- É representado através de uma linha imaginária.

- É medido em metros.

- É uma quantidade escalar.

- Não leva em consideração o caminho viajado.

- Considere o tempo gasto durante o passeio.

- Depende de um sistema de referência.

- Quando o ponto de partida ou a posição inicial é a mesma que a posição final, a trajetória é dada pela distância percorrida.

- O valor da trajetória coincide com o módulo do deslocamento do vetor, se a trajetória resultante for uma linha reta, mas não há mudanças no sentido a seguir.

- Sempre aumenta quando o corpo se move, independentemente da trajetória.

Referências

1. Fernández, m., Fidalgo, J. (2016). Física e química 1º bacharelado. Edições paraninfo, S.PARA. Espanha.
2. Instituto Guatemalteco de Educação de Rádio (2011) Física Fundamental. Grupo Zaculeu do primeiro semestre. Guatemala.