O que é um experimento determinístico?

Ele experimento determinístico, Nas estatísticas, é um que possui um resultado previsível e reproduzível, desde que as mesmas condições iniciais e parâmetros sejam mantidas. Isto é, a relação causa-efeito é conhecida em sua totalidade.

Por exemplo, o tempo que leva a areia de um relógio para se mover de um compartimento para o outro é um experimento determinístico, porque o resultado é previsível e reproduzível. Enquanto as condições forem iguais, levará o mesmo tempo para passar de cápsula para cápsula.

figura 1. O tempo que leva a areia de um compartimento para o outro é um experimento determinístico. Fonte: Pixabay

Muitos fenômenos físicos são determinísticos, sendo alguns exemplos os seguintes:

- Um objeto mais denso que a água, como uma pedra, sempre afundará.

- Um flutuador, que é menos denso que a água, sempre estará à tona (a menos que uma força que a mantenha submersa) é exercida).

- A temperatura de ebulição da água no nível do mar é sempre 100 ºC.

- O tempo que leva para cair dado que cai do descanso, pois é determinado pela altura da qual foi descartado e desta vez é sempre o mesmo (quando é liberado da mesma altura).

Aproveitando o exemplo dos dados. Se isso for descartado, mesmo quando você tiver o cuidado de dar a mesma orientação e sempre na mesma altura, é difícil prever o rosto que aparecerá assim que ela parar no chão. Este seria um experimento aleatório.

Teoricamente, se eles eram conhecidos com dados de precisão infinita, como: posição; velocidade inicial e orientação dos dados; forma (bordas arredondadas ou angulares); e coeficiente de restituição da superfície em que cai, talvez fosse possível prever, através de cálculos complexos, o que o rosto dos dados mostrará quando parar. Mas qualquer pequena variação nas condições de partida daria um resultado diferente. 

Tais sistemas são determinísticos e, ao mesmo tempo.

Pode atendê -lo: Sistema de equações: métodos de solução, exemplos, exercícios

[TOC]

Medição

Os experimentos determinísticos são completamente mensuráveis, mas ainda assim a medição de seu resultado não é infinitamente precisa e tem uma certa margem de incerteza.

Vamos colocar, por exemplo, o experimento a seguir, totalmente determinístico: solte um carro de brinquedo em uma inclinação reta.

Figura 2. Um carro desce através de uma inclinação retilínea em um experimento determinístico. Fonte: Pixabay.

É sempre liberado do mesmo ponto de partida, tomando cuidado para não dar nenhum impulso. Nesse caso, o tempo que leva o carro a percorrer a pista deve sempre ser o mesmo.

Agora, uma criança pretende medir o tempo que leva para o carrinho Tour the Track. Para isso, você usará o cronômetro que é incorporado ao seu telefone celular.

Sendo um garoto observador, a primeira coisa que você observa é que seu instrumento de medição tem uma precisão finita, porque a menor diferença de tempo que pode medir o cronômetro é 1 centésimo de segundo.

Em seguida, a criança passa a realizar o experimento e com o Mobile Stopwatch mede 11 vezes - digamos que, com certeza - o tempo que levou ao carrinho para viajar pelo plano inclinado, obtendo os seguintes resultados:

3,12s 3,09S 3,04S 3,04S 3.10S 3.08S 3.05S 3.10S 3.11s 3.06s e 3.03s.

A criança fica surpresa, porque na escola eles lhe disseram que este é um experimento determinístico, mas em cada extensão ele obteve um resultado ligeiramente diferente.

Variações na medida

Quais podem ser as causas que em cada medição têm um resultado diferente? 

Uma causa pode ser a precisão do instrumento, que como já havia sido dito é 0,01s. Mas observe que as diferenças nas medições estão acima desse valor, portanto, deve -se pensar em outras causas, como:

- Pequenas variações do ponto de partida.

- Diferenças no início e parada do cronômetro, devido ao tempo de reação da criança.

Em relação ao tempo de reação, certamente ocorre um atraso, já que a criança vê que o carrinho começa a se mover, até que o cronômetro pressiona. 

Pode servir você: bordas de um cubo

Da mesma forma, na chegada, há um atraso devido ao tempo à reação. Mas os atrasos de início e chegada são compensados, para que o tempo obtido seja muito próximo do real. 

De qualquer forma, a compensação pelo atraso da reação não é exata, porque os tempos de reação podem ter pequenas variações em cada estudo, o que explica as diferenças nos resultados.

Qual é então o verdadeiro resultado do experimento?

Resultados de uma medição e erro

Para relatar o resultado final, devemos usar estatísticas. Primeiro, vamos ver com que frequência os resultados são repetidos:

- 3.03s (1 hora)

- 3.04s (2 vezes)

- 3.05s (1 tempo)

- 3.06s (1 tempo)

- 3.08s (1 hora)

- 3.09s 1 tempo

- 3.10s (2 vezes)

- 3.11s (1 hora)

- 3.12s (1 hora)

Ao pedir os dados, percebemos que um moda ou resultado mais repetido. Então o resultado a ser relatado é a média aritmética, que pode ser calculada da seguinte forma:

(1 × 3,03 + 2 × 3,04 + 1 × 3,05 + 1x 3,06 + 1 × 3,08 + 1 × 3,09 + 2 × 3,10 + 1 × 3,11 + 1 × 3,12) / (1 + 2 + 1 + 1 + 1 + 1 + 2 + 1 + 1).

O resultado do cálculo anterior é 3.074545455. Logicamente, não faz sentido relatar todas essas decimais no resultado, porque cada medição não tem nada mais 2 decimais de precisão. 

Aplicando as regras de arredondamento, pode -se dizer que o tempo que leva para a turnê do carrinho a pista é a média aritmética arredondada para duas figuras decimais.

O resultado que podemos relatar para o nosso experimento é:

3,08 segundos é o tempo que você leva para o carro de brinquedo viaja pela pista inclinada.

- Erro de medição

Como visto em nosso exemplo de um experimento determinístico, toda medição tem um erro, pois não pode ser medido com precisão infinita.

De qualquer forma, a única coisa que pode ser feita é melhorar os instrumentos e métodos de medição, a fim de obter um resultado mais preciso.

Na seção anterior, demos um resultado para o nosso experimento determinístico do tempo que leva ao carro de brinquedo para viajar uma pista inclinada. Mas este resultado implica um erro. Agora vamos explicar como calcular esse erro.

Pode servir a você: Coordenadas retangulares: Exemplos e exercícios resolvidos

- Cálculo do erro de medição

Nas medições do tempo, há uma dispersão nas medidas feitas. O Desvio padrão É um formulário estatístico frequentemente usado para relatar a dispersão de dados. 

Variação e desvio padrão

A maneira de calcular o desvio padrão é assim: primeiro é a variação dos dados, definida desta maneira:

A soma das diferenças de cada resultado com a média aritmética, quadrada e dividida pelo número total de dados

Se a raiz quadrada for levada para a variação, o desvio padrão será obtido.

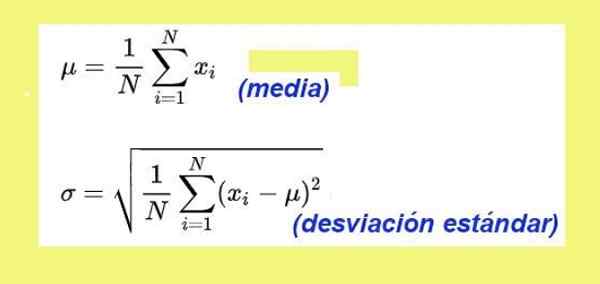Figura 3. Fórmulas médias e desvio padrão. Fonte: Wikimedia Commons.

O desvio padrão para os dados de tempo de descida do Toy Auton é:

σ = 0,03

O resultado foi arredondado para 2 decimais, porque a precisão de cada um dos dados é de 2 decimais. Nesse caso, 0,03s representa o erro estatístico de cada um dos dados.

No entanto, a média aritmética média dos tempos obtidos tem um erro menor. O erro médio é calculado dividindo o desvio padrão entre a raiz quadrada do número total de dados.

Erro médio = σ / √n = 0,03 / √11 = 0,01

Isto é, o erro estatístico do tempo médio é 1 centésimo de segundo e neste exemplo, coincide com a apreciação do cronômetro, mas nem sempre é assim.

Como resultado final da medida, é relatado então:

 T = 3,08s ± 0,01s é o tempo que leva para o carro de brinquedo para viajar pela pista inclinada.

Conclui -se que, mesmo quando se trata de um experimento determinístico, o resultado de sua medição não tem precisão infinita e sempre tem uma margem de erro. 

Além disso, para relatar o resultado final, é necessário, mesmo quando se trata de um experimento determinístico, use métodos estatísticos.

Referências

1. Canalphi. Experimento determinístico. Recuperado de: youtube.com
2. Mathemovil. Experimento determinístico. Recuperado de: youtube.com
3. Pishro nick h . Introdução à probabilidade. Recuperado de: ProbabilityCourse.com
4. Ross. Probabilidade e estatística para engenheiros. Mc-Graw Hill.
5. Estatísticas como. Determinista: Definição e Exames. Recuperado de: statisticshowto.DataScienceCeral.com
6. Wikipedia. Desvio típico. Recuperado de: é.Wikipedia.com
7. Wikipedia. Experiência (teoria da probabilidade). Recuperado de: em.Wikipedia.com