Fórmulas de distribuição de Poisson, equações, modelo, propriedades

O Distribuição de veneno É uma distribuição de probabilidades discretas, através da qual você pode saber a probabilidade de que, dentro de uma amostra grande e durante um determinado intervalo, um evento cuja probabilidade é pequena ocorra.

Freqüentemente, a distribuição de Poisson pode ser usada em vez da distribuição binomial, desde que as seguintes condições descritas sejam atendidas: amostra grande e pequena probabilidade.

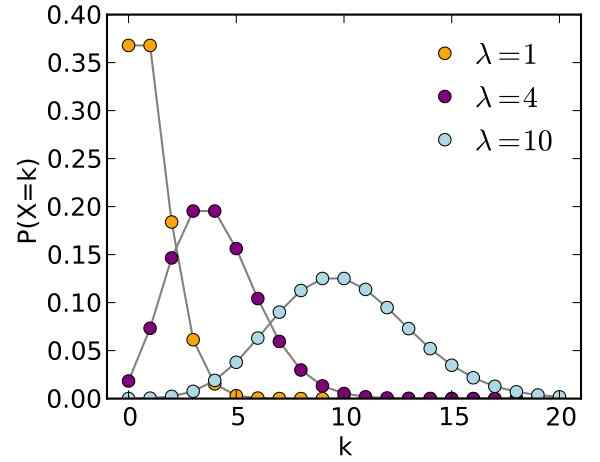
figura 1. Gráfico de distribuição de Poisson para diferentes parâmetros. Fonte: Wikimedia Commons.

Siméon-denis Poisson (1781-1840) criou essa distribuição que leva seu nome, muito útil quando se trata de eventos imprevisíveis. Poisson publicou seus resultados em 1837, um trabalho de pesquisa sobre a probabilidade de ocorrência de sentenças criminais errôneas.

Posteriormente, outros pesquisadores adaptaram a distribuição em outras áreas, por exemplo, o número de estrelas que poderiam estar em um certo volume de espaço, ou a probabilidade de um soldado morrer por causa de um cavalo porque.

[TOC]

Fórmula e equações

A forma matemática da distribuição de Poisson é a seguinte:

 - A variável aleatória é e

- μ (também às vezes indicado como λ) É o parâmetro médio ou de distribuição

- Número Euler: E = 2.71828

- A probabilidade de obter y = k é p

- k É o número de sucessos 0, 1,2,3 ..

- n É o número de testes ou eventos (tamanho da amostra)

As variáveis ​​aleatórias discretas, como o nome indica, dependem do acaso e apenas tomam valores discretos: 0, 1, 2, 3, 4 ..., k.

A média da distribuição é dada por:

A variação σ, que mede a dispersão dos dados, é outro parâmetro importante. Para a distribuição de Poisson, é:

σ = μ

Poisson determinou que quando n → ∞ e p → 0, o μ -tal também chamado valor esperado- Tende a uma constante:

μ → Constante

Importante: p É a probabilidade de ocorrência do evento levar em consideração a população total, enquanto P (Y) É a previsão de Poisson sobre a amostra.

Modelo e propriedades

A distribuição de Poisson tem as seguintes propriedades:

-O tamanho da amostra é grande: N → ∞.

-Os eventos ou eventos considerados são independentes um do outro e ocorrem aleatoriamente.

-Probabilidade P Que certo evento e Ocorre por um período específico de tempo é muito pequeno: P → 0.

-A probabilidade de mais de um evento no intervalo de tempo é 0.

-O valor médio está próximo de uma constante dada por: μ = n.P (n é o tamanho da amostra)

-Como a dispersão σ é igual a μ, pois adota valores maiores, a variabilidade também é maior.

-Os eventos devem ser distribuídos uniformemente no intervalo de tempo usado.

-O conjunto de possíveis valores de evento e É: 0,1,2,3,4 .. .

Pode servir a você: experimento aleatório: conceito, espaço de amostra, exemplos

-A soma de Yo Variáveis ​​que seguem uma distribuição de Poisson, também é outra variável de Poisson. Seu valor médio é a soma dos valores médios dessas variáveis.

Diferenças com a distribuição binomial

A distribuição de Poisson difere da distribuição binomial nos seguintes aspectos importantes:

-A distribuição binomial é afetada tanto pelo tamanho da amostra S quanto pela probabilidade P, Mas a distribuição de Poisson é afetada apenas pela média μ.

-Em uma distribuição binomial, os possíveis valores da variável aleatória e Eles são 0,1,2,…, em vez da distribuição de Poisson, não há limite superior para esses valores.

Exemplos

Poisson aplicou inicialmente sua famosa distribuição a casos legais, mas no nível industrial, um de seus primeiros usos foi na fabricação de cerveja. Neste processo, as culturas de leveduras são usadas para fermentação.

O fermento consiste em células vivas, cuja população é variável no tempo. Na fabricação de cerveja, é necessário adicionar a quantidade necessária, por isso é necessário saber a quantidade de células por unidade de volume.

Durante a Segunda Guerra Mundial, a distribuição de Poisson foi usada para saber se os alemães estavam realmente apontando para Londres de Calais, ou simplesmente disparando aleatoriamente. Isso foi importante para os Aliados determinarem como era boa a tecnologia disponível para os nazistas.

Aplicações práticas

Os aplicativos de distribuição de Poisson sempre se referem às contagens de tempo ou contagens de espaço. E como a probabilidade de ocorrência é pequena, também é conhecida como "Lei de Eventos Raros".

Aqui está uma lista de eventos que se enquadram em uma dessas categorias:

-O registro de partículas em um decaimento radioativo, que, como o crescimento de células de levedura, é uma função exponencial.

-Número de visitas a um determinado site.

-Chegada de pessoas à uma briga para pagar ou ser atendida (teoria das caudas).

-Número de carros que passam por um certo ponto em uma estrada, para um determinado intervalo de tempo.

Figura 2. A quantidade de carros que passam por um ponto segue aproximadamente uma distribuição de Poisson. Fonte: Pixabay.

-Mutações sofreram em uma certa cadeia de DNA após receber a exposição à radiação.

-Número do meteoro de diâmetro superior a 1 m caído em um ano.

-Defeitos por metro quadrado de um tecido.

-Quantidade de células sanguíneas em 1 centímetro cúbico.

-Ligações por minuto para uma bolsa telefônica.

-Faíscas de chocolate presentes em 1 kg de massa de bolo.

-Número de árvores infectadas pelo caminho em 1 hectare da floresta.

Observe que essas variáveis ​​aleatórias representam o número de vezes que um evento acontece por um período fixo de tempo (Ligações por minuto para a bolsa telefônica), ou uma determinada região do espaço (Defeitos de um tecido por metro quadrado).

Pode atendê -lo: variação proporcional

Esses eventos, como já estabelecidos, são independentes do tempo que passou desde a última ocorrência.

Aproximando -se da distribuição binomial com a distribuição de Poisson

A distribuição de Poisson é uma boa abordagem para a distribuição binomial enquanto:

-O tamanho da amostra é grande: n ≥ 100

-Probabilidade P é pequeno: p ≤ 0,1

- μ estar na ordem de: NP ≤ 10

Nesses casos, a distribuição de Poisson é uma excelente ferramenta, uma vez que a distribuição binomial pode se tornar complicada de aplicar nesses casos.

Exercícios resolvidos

Exercício 1

Um estudo sismológico determinou que, durante os últimos 100 anos, houve 93 grandes terremotos em todo o mundo, pelo menos 6.0 na escala Richter -logarítmica-. Suponha que a distribuição de Poisson seja um modelo adequado neste caso. Encontrar:

a) A ocorrência média de grandes terremotos por ano.

b) Sim P (Y) É a probabilidade de acontecer e Terremotos para um ano selecionado aleatório, encontre as seguintes probabilidades:

P(0), P(1), P (2), P (3), P (4), P (5), P (6) e P (7).

c) Os verdadeiros resultados do estudo são os seguintes:

- 47 anos (0 terremotos)

- 31 anos (1 terremoto)

- 13 anos (2 terremotos)

- 5 anos (3 terremotos)

- 2 anos (4 terremotos)

-  0 anos (5 terremotos)

- 1 ano (6 terremotos)

- 1 ano (7 terremotos)

Como esses resultados são obtidos na subseção B? A distribuição de Poisson é uma boa escolha para modelar esses eventos?

Solução para)

a) terremotos são eventos cuja probabilidade p Ele é pequeno e estamos considerando um período de tempo restrito, de um ano. Os terremotos médios são:

μ = 93 /100 terremotos / ano = 0.93 terremotos por ano.

Solução b)

b) Para calcular as probabilidades solicitadas, os valores são substituídos na fórmula dada no início:

Por exemplo, para encontrar P (2), Qual seria a probabilidade de haver 2 grandes terremotos por ano:

y = 2

μ = 0.93

E = 2.71828

E essa é a probabilidade de que haja 7 grandes terremotos por um ano:

É bem menor que P (2).

Os resultados estão listados abaixo:

P (0) = 0.395, p (1) = 0.367, p (2) = 0.171, p (3) = 0.0529, p (4) = 0.0123, p (5) = 0.00229, p (6) = 0.000355, p (7) = 0.0000471.

Por exemplo, poderíamos dizer que há uma probabilidade de 39.5 % que nenhum grande terremoto ocorre em um determinado ano. Ou que existem 5,29 % que 3 grandes terremotos ocorrem naquele ano.

Solução c)

c) As frequências são analisadas, multiplicando -se por n = 100 anos:

39.5; 36.7; 17.1; 5.29; 1.23; 0.229; 0.0355 e 0.00471.

Pode atendê -lo: derivados algébricos

Por exemplo:

- Uma frequência de 39.5 indica que, em 39.Ocorrem 5 de 100 anos ou grandes terremotos, poderíamos dizer que está bem perto do resultado real de 47 anos, sem qualquer grande terremoto.

Vamos comparar outro resultado de Poisson com resultados reais:

- O valor obtido de 36.7 significa que em um período de 37 anos há 1 grande terremoto. O resultado real é que em 31 anos houve 1 grande terremoto, uma boa coincidência com o modelo.

- 17 são esperados.1 ano com 2 grandes terremotos e sabe -se que em 13 anos, o que é um valor próximo, houve de fato 2 grandes terremotos.

Portanto, o modelo de Poisson é aceitável para este caso.

Exercício 2

Uma empresa estima que o número de componentes que falham antes de concluir 100 horas de operação segue uma distribuição de Poisson. Se o número médio de falhas for 8 naquele momento, encontre as seguintes probabilidades:

a) Que um componente falha em 25 horas.

b) Falha menos de dois componentes, em 50 horas.

c) Que pelo menos três componentes falham em 125 horas.

Solução para)

a) Sabe -se que a falha média em 100 horas é 8, portanto, em 25 horas, a quarta parte das falhas é esperada, ou seja, 2 falhas. Este será o parâmetro μ.

A probabilidade de falhar 1 componente é solicitado, a variável aleatória é “componentes que falham antes de 25 horas” e seu valor é y = 1. Substituindo a função de probabilidade:

 b) Agora a variável aleatória é "componentes que falham antes de 50 horas". O parâmetro é μ = 4, Como o valor esperado das falhas em 50 horas é 4.

No entanto, a questão é a probabilidade de que menos de dois componentes falhem em 50 horas, não que exatamente 2 componentes falhem em 50 horas; portanto, devemos adicionar as probabilidades que:

-Nenhum falha

-Falhar apenas 1

P (menos de 2 componentes) = p (0) + p (1)

P (menos de 2 componentes) = 0.0183+0.0732 = 0.0915

c) Que pelo menos 3 componentes falham em 125, significa que 3, 4, 5 ou mais naquele momento podem falhar.

A probabilidade de ocorrer pelo menos um dos vários eventos é igual a 1, exceto a probabilidade de que nenhum dos eventos aconteça.

-O evento procurado é falhar 3 ou mais componentes em 125 horas

-O fato de o evento não acontecer significa que menos de 3 componentes falham, cuja probabilidade é: P (0)+p (1)+p (2)

O parâmetro μ da distribuição neste caso é:

 μ = 8 + 2 = 10 falhas em 125 horas.

P (caído 3 ou mais componentes) = 1- P (0)- P (1)- P (2) =

= 1-0.0026786 = 0.9972

Referências

1. Mathworks. Distribuição de veneno. Recuperado de: é.Mathworks.com
2. Mendenhall, w. 1981. Estatística para administração e economia. 3º. edição. Grupo editorial da Iberoamerica.
3. Stat Trek. Ensine a si mesmo estatísticas. Distribuição de veneno. Recuperado de: stattrek.com,
4. TRIOLA, m. 2012. Estatísticas elementares. 11º. Ed. Pearson Education.
5. Wikipedia. Distribuição de veneno. Recuperado de: em.Wikipedia.org