Fórmulas de coeficiente de correlação, cálculo, interpretação, exemplo

Ele coeficiente de correlação Nas estatísticas, é um indicador que mede a tendência de duas variáveis ​​quantitativas x e y ter uma relação de linearidade ou proporcionalidade entre elas.

Geralmente, os pares de variáveis ​​x e y são duas características da mesma população. Por exemplo, x pode ser a altura de uma pessoa e e seu peso.

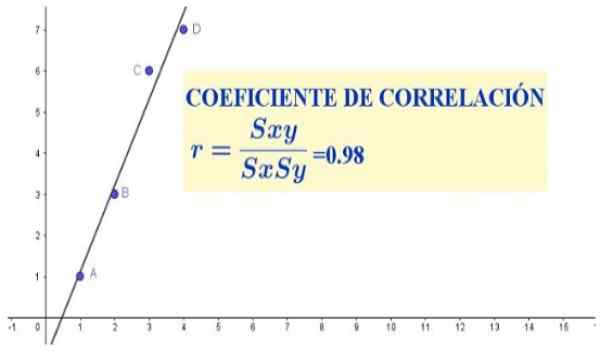
figura 1. Coeficiente de correlação para quatro pares de dados (x, y). Fonte: f. Zapata.

Nesse caso, o coeficiente de correlação indicaria se há ou não uma proporção de proporcionalidade entre a altura e o peso de uma determinada população.

O coeficiente de correlação linear de Pearson é indicado com a carta r minúsculas e seus valores mínimo e máximo são -1 e +1, respectivamente. 

Um valor r = +1 indicaria que todo o pares (x, y) está perfeitamente alinhado e que quando x crescer, e crescerá na mesma proporção. Por outro lado, se isso acontecer que r = -1, o conjunto de pares também estaria perfeitamente alinhado, mas nesse caso quando X cresce e diminui na mesma proporção.

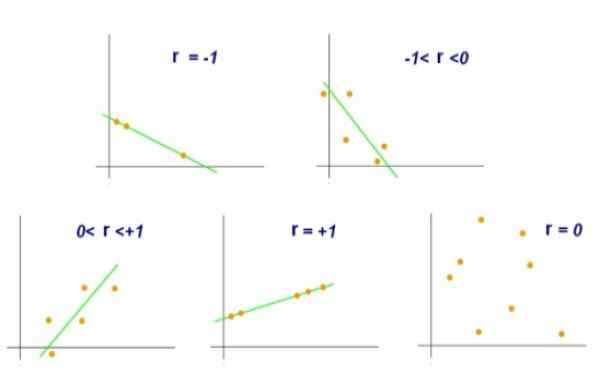Figura 2. Diferentes valores do coeficiente de correlação linear. Fonte: Wikimedia Commons.

Por outro lado, um valor r = 0 indicaria que não há correlação linear entre as variáveis ​​x e y. Embora um valor de r = +0,8 indique que os pares (x, y) tendem a agrupar para um lado e outro de uma certa linha.

A fórmula para calcular o coeficiente de correlação R é a seguinte:

Onde o numerador representa a covariância entre as variáveis ​​x e y, enquanto o denominador é o produto do desvio padrão para a variável x e o desvio padrão para a variável e.

Como calcular o coeficiente de correlação?

O coeficiente de correlação linear é uma quantidade estatística que é incorporada a calculadoras científicas, na maioria das planilhas e programas estatísticos.

Pode servir a você: parabolóide hiperbólico: definição, propriedades e exemplos

No entanto, é conveniente saber como a fórmula que define é aplicada e, para isso, um cálculo detalhado será exibido, realizado em um pequeno conjunto de dados.

E, como afirmado na seção anterior, o coeficiente de correlação é a covariância SXY dividida pelo produto do desvio padrão SX para as variáveis ​​x e sy para a variável e.

Covariância e variação

A covariância SXY é:

Sxy = [σ (xi -) (yi -)] / (n -1)

Onde a soma vai de 1 para os n pares (xi, yi). E são as meias aritméticas dos dados xi e yi, respectivamente.

Por sua parte, o desvio padrão para a variável x é a raiz quadrada da variação do conjunto de dados xi, com I de 1 a n:

Sx = √ [σ (xi -)^2) / (n -1)]

Da mesma forma, o desvio padrão para a variável e é a raiz quadrada da variação do conjunto de dados YI, com I de 1 a n:

Sy = √ [σ (yi -)² ) / (N-1)]

Caso ilustrativo

Para mostrar em detalhes a maneira de calcular o coeficiente de correlação, levaremos o seguinte conjunto de quatro pares de dados 

(X, y): (1, 1); (23); (3, 6) e (4, 7).

Primeiro, calculamos a média aritmética para x e y, como segue:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Em seguida, os demais parâmetros são calculados:

SXY Covariância

Sxy = [(1 - 2.5) (1 - 4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. ... .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Pode atendê -lo: regras de derivação (com exemplos)

.. .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Desvio padrão sx

Sx = √ [(-1.5)² + (-0.5)² + (0.5)² + (1.5)²) / (4-1)] = √ [5/3] = 1.29

Desvio padrão sy

Sx = √ [(-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (4-1)] = 

√ [22.75/3] = 2.75

Coeficiente de trilhos r

R = 3.5 / (1.29 * 2.75) = 0.98

Interpretação

No conjunto de dados do caso anterior, há uma forte correlação linear entre as variáveis ​​x e y, que se manifesta tanto no gráfico de dispersão (que pode ser visto na Figura 1) e no coeficiente de correlação, que jogou um valor bem próximo a a unidade.

Na medida em que o coeficiente de correlação está mais próximo de 1 ou -1, mais sentido faz com que a configuração dos dados em uma linha, o resultado da regressão linear.

Regressão linear

A linha de regressão linear é obtida de Método de mínimos quadrados. em que o parâmetro da linha de regressão é obtido a partir da minimização da soma do quadrado da diferença entre o valor e estimado e o yi dos dados n.

Por outro lado, os parâmetros A e B da linha de regressão y = a + bx, obtidos pelo método dos quadrados mínimos, são:

*B = sxy / (sx²) Para a inclinação

*A = - b para a interseção da linha de regressão com o eixo do e.

Lembre -se de que SXY é a covariância definida acima e SX² É a variação ou o quadrado do desvio padrão definido anteriormente. E são os meios aritméticos dos dados x e e respectivamente.

Exemplo

O coeficiente de correlação é usado para determinar se existe uma correlação do tipo linear entre duas variáveis. É aplicável quando as variáveis ​​a serem estudadas são quantitativas e também, elas devem seguir uma distribuição de tipo normal.

Pode atendê -lo: regra de correspondência de uma função

Um exemplo ilustrativo que temos abaixo: Uma medida do grau de obesidade é o índice de massa corporal, obtido dividindo o peso de uma pessoa em quilogramas entre a altura da mesma nas unidades quadradas do quadrado.

É desejado saber se existe uma forte correlação entre o índice de massa corporal e a concentração de colesterol HDL no sangue, medido em milimoles por litro. Para esse fim, um estudo foi realizado com 533 pessoas resumidas no gráfico a seguir, no qual cada ponto representa os dados de uma pessoa.

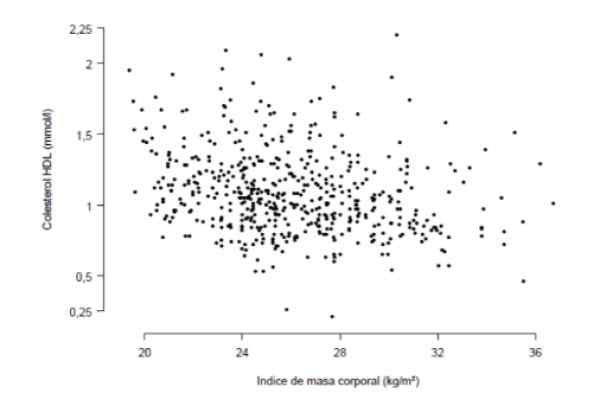Figura 3. Estudo IMC e colesterol HDL em 533 pacientes. Fonte: Instituto Aragonês de Ciências da Saúde (IACS).

A partir da observação cuidadosa do gráfico, segue -se que existe uma certa tendência linear (não muito marcada) entre a concentração de colesterol HDL e o índice de massa corporal. A medida quantitativa dessa tendência é o coeficiente de correlação que, para este caso, acabou sendo r = -0.276.

Referências

1. González c. Estatísticas gerais. Recuperado de: tarwi.La molina.Edu.educaçao Fisica
2. IACS. Instituto Aragonês de Ciências da Saúde. Recuperado de: ICS-Aragon.com 
3. Salazar c. e Castillo s. Princípios de estatísticas básicas. (2018). Recuperado de: dspace.Uce.Edu.EC
4. Superprof. Coeficiente de correlação. Recuperado de: superprof.é
5. USAC. Manual de Estatística Descritiva. (2011). Recuperado de: estatísticas.Engenharia.USAC.Edu.Gt
6. Wikipedia. Coeficiente de correlação de Pearson. Recuperado de: é.Wikipedia.com.