Produto cruzado

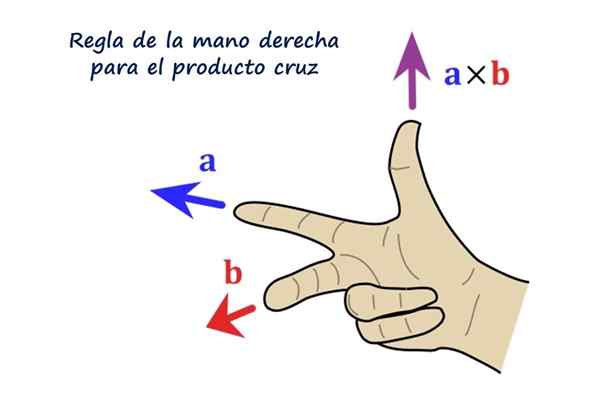Regra correta para o produto vetorial. Fonte: f. Zapata.

Qual é o produto cruzado ou produto vetorial?

Ele Produto cruzado, Também chamado de produto vetorial, é um tipo de produto que é realizado entre dois vetores e resulta em outro vetor, perpendicular ao plano definido pelos dois primeiros.

O produto cruzado entre dois vetores para e b, Resulta em outro vetor R, Matematicamente está escrito da seguinte maneira:

para × b = R

É assim: “Um cruzamento B igual a R ".

No texto impresso, os vetores são escritos com letras ousadas, ou com uma flecha na carta, para distingui -las de sua magnitude ou módulo. Para isso, eles são usados, de forma intercambiável, barras de módulos e letras atuais; portanto, o valor absoluto do vetor para O símbolo está escrito assim:

│para│ = a

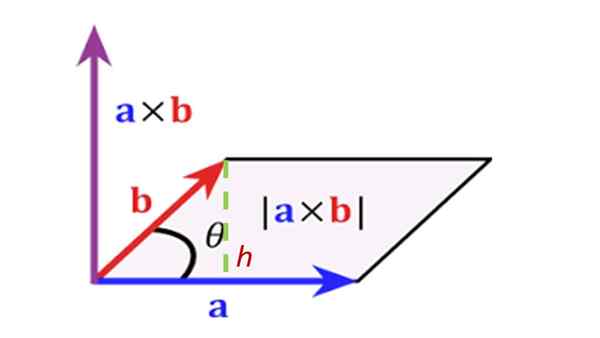
O valor ou módulo absoluto do produto vetorial entre dois vetores é calculado multiplicando o módulo de ambos os vetores através do ângulo θ entre eles:

R = a ∙ b ∙ sen θ

A direção do vetor R É perpendicular ao dos vetores para e b. O sentido de R É dextrogyr de para na direção b E, na prática, é determinado usando a regra da mão direita, que consiste em posicionar o índice, médio e polegar da mão direita da seguinte forma:

• O dedo indicador é colocado seguindo o vetor para
• Com o dedo médio segue o vetor b
• O polegar, estendido, indica a direção e a direção do vetor R.

Esta ordem deve ser seguida exatamente, uma vez que o produto vetorial não é comutativo, isto é para × b ≠ b × para E se os vetores forem trocados, o resultado correto não será obtido.

Pode atendê -lo: Teorema da existência e exclusividade: demonstração, exemplos e exercícios

O leitor é aconselhado a colocar a mão direita como a figura mostra, o índice apontando para a esquerda representa o vetor para, O dedo médio segue b E aponta diretamente para o leitor, finalmente, o polegar indica, apontando para a direção e direção do vetor para × b = R.

Propriedades do produto Cruz

-O produto cruzado ou vetorial entre dois vetores sempre resulta em outro vetor.

-Um produto cruzado não é comutativo, portanto: para × b ≠ b × para.

-Para o produto cruzado, é verdade que: para × b = - (b × para). Esta propriedade é chamada Anti-Connminacy.

-O vetor resultante do produto vetorial entre dois vetores é perpendicular (normal) aos referidos vetores.

-Do exposto, segue -se que o produto vetorial entre vetores com a mesma direção é nulo. Em particular para × A = 0.

-O produto cruzado está em conformidade com a lei de distribuição em relação à soma: para × (b+c) = para × b + para × c

-Se m é um escalar, então m (para × b) = m para × b = para × m b

PRODUTO CRIME

Os três vetores de unidade, chamados Yo, J e k, Eles são perpendiculares um ao outro e indicam as três direções notáveis ​​do espaço: alto, largo e profundidade. Esses endereços são perpendiculares um ao outro.

O produto vetorial entre os vetores da unidade é facilmente determinado pela regra da mão direita e tendo em mente as propriedades do produto cruzado:

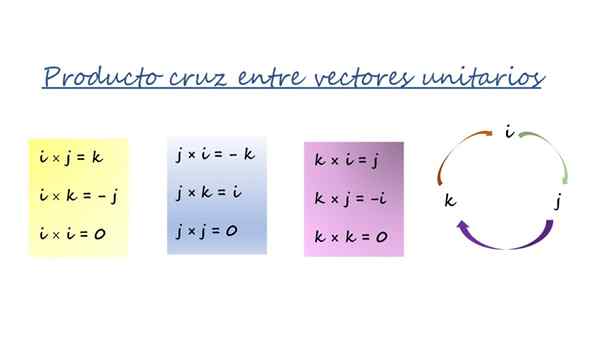Produto vetorial de vetores unitários cartesianos. Fonte: f. Zapata.

As três caixas coloridas da figura estão resumidas na rodada com setas à direita e são usadas dessa maneira:

-Ao se multiplicar na direção da seta, o resultado é o vetor em frente à flecha e tem um sinal positivo. Por exemplo, multiplicando vetorialmente J e k, O terceiro vetor é Yo, E como a ordem segue o significado da flecha, o sinal é +.

Pode atendê -lo: funções vetoriais

-E se multiplicar na direção oposta à seta, o resultado é o terceiro vetor na frente da seta, mas com um sinal negativo.

Os vetores da unidade constituem uma base, para que qualquer outro vetor possa ser escrito em termos deles. Isso facilita muito o cálculo do produto cruzado entre dois vetores arbitrários no espaço.

Como analisar o produto cruzado de dois vetores analiticamente

Quando vetores para e b Eles têm uma direção arbitrária no espaço, com componentes ao longo de cada um deles, é mais fácil calcular o produto cruzado de maneira analítica, expressando -os em termos dos vetores da unidade Yo, J e k:

• para = a_x Yo + para_e J + para_z k
• b = b_x Yo + b_e J + b_z k

Agora, a propriedade distributiva da multiplicação é usada, que também é válida para o produto cruzado:

para × b = (a_x Yo + para_e J + para_z k) × (b_x Yo + b_e J + b_z k) =

= (a_x Yo × b_x Yo) + (A_x Yo × b_e J) + (A_x Yo × b_z k) + (A_E J × b_x Yo) + (A_E J × b_e J) + (A_E J × b_z k) + (A_Z k × b_x Yo) + (A_Z k × b_e J) + (A_Z k × b_z k)

Os produtos cruzados entre os vetores unitários iguais são cancelados, pois são vetores paralelos, o que reduz essa expressão a 6 termos:

para × b = (a_x Yo × b_e J) + (A_x Yo × b_z k) + (A_E J × b_x Yo) + (A_E J × b_z k) + (A_Z k × b_x Yo) + (A_Z k × b_e J)

Finalmente, usando a figura acima, cada produto resulta em:

para × b = a_x b_e k + para_x b_z ( -J) + a_E b_x ( -k) + a_E b_z Yo + para_Z b_xJ + para_Z b_e ( -Yo) =

= (a_E b_z - a_Z b_e) Yo + (para_Z b_x - a_x b_z) J + (para_x b_e - a_E b_x) k

Produto Cruz através de um determinante

Não é necessário memorizar a fórmula acima, mas aplicar convenientemente a rodada da figura anterior ou simplesmente realizar cuidadosamente o determinante mostrado abaixo, que é totalmente equivalente:

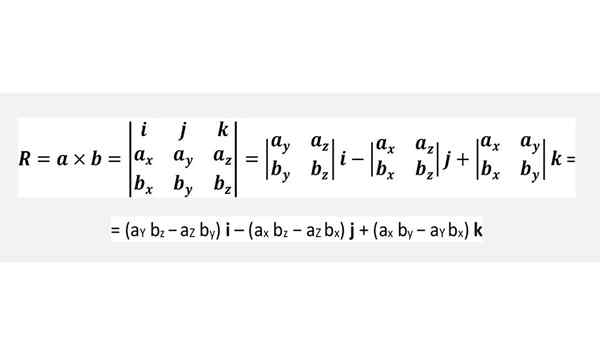
Exemplo

Assumindo vetores para e b são:

• para = 5 Yo - J + 4 k
• b = -Yo + 0J +7 k

O produto cruzado entre eles é calculado identificando e substituindo as respectivas coordenadas:

Pode servir a você: parabolóide hiperbólico: definição, propriedades e exemplos

para_x = 5; para_e = −1; para_z = 4; b_x = −1; b_e = 0: b_z = 7

para × b = [(−1) ∙ 7 - 4 ∙ 0] Yo + [(4 ∙ (−1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] k = [−7 - 0] Yo + [(-4 - 35) J + [0 - 1] k =

= (-7) Yo - 39 J - k

O método determinante oferece o mesmo resultado.

Exercício

Calcule pelos determinantes, o produto cruzado entre os vetores:

• ou = 2 Yo +J + 5 k
• v = Yo + 4J +7 k

E determine a área do paralelogramo subtendida pelos vetores anteriores, como mostrado na figura:

Solução

Os valores das coordenadas dos valores são substituídos no determinante:

A área de paralelogramo determinada é o módulo do produto vetorial entre eles, resultante: r = 17,3 unidades de área.