Números inteiros

O que são números inteiros?

Números inteiros constituem um conjunto de números úteis para contar os objetos completos que são obtidos e aqueles que não são. Também para contar aqueles de um lado e o outro de um determinado local de referência.

Também com os números inteiros, a subtração ou diferença pode ser realizada entre um número e outro maior que ele, sendo resolvido como uma dívida, por exemplo. A distinção entre lucros e dívidas é feita com sinais + e - respectivamente.

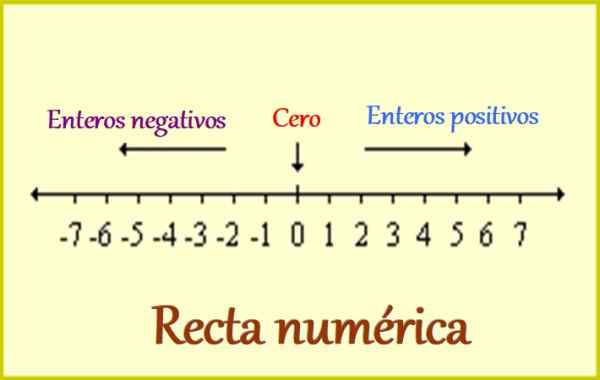
figura 1. A linha numérica para números inteiros. Fonte: Wikimedia Commons. LEOMG/CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0).

É por isso que todo o número inteiro inclui o seguinte:

-Números inteiros positivos, que são escritos precedidos por um sinal de A +, ou simplesmente sem o sinal, pois também é entendido que eles são positivos. Por exemplo: +1, +2, +3 ... e assim por diante.

-O 0, no qual o sinal é irrelevante, porque não o adiciona para subtrair de alguma quantidade. Mas o 0 é muito importante, pois é a referência para os números inteiros: de um lado, os positivos estão localizados e os negativos, como vemos na figura superior.

-Inteiros negativos, que sempre devem ser escritos a partir do sinal -, pois com eles as quantidades como dívidas e todos aqueles que estão do outro lado da referência são distintos. Exemplos de números inteiros negativos são: -1, -2, -3 ... e a partir de então.

Como são os números inteiros?

No início, representamos os números inteiros com a configuração do conjunto: z = … -4, -3, -2, -1, 0, +1, +2, +3, +4…, isto é, listado e organizado. Mas uma representação muito útil é o que usa a linha numérica. Para isso, é necessário desenhar uma linha, que geralmente é horizontal, na qual 0 é marcado e dividido em seções idênticas:

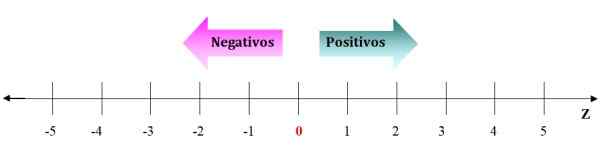Figura 2. Representação de números inteiros na linha numérica. De 0 à direita são os números inteiros positivos e de 0 para a esquerda os negativos. Fonte: f. Zapata.

Os negativos vão para a esquerda de 0 e os positivos vão para a direita. As setas na linha numérica simbolizam que os números continuam para o infinito. Dado qualquer número inteiro, é sempre possível encontrar um que seja maior ou diferente de.

O valor absoluto de um número inteiro

O valor absoluto de um número inteiro é a distância entre o número e 0. E as distâncias são sempre positivas. Portanto, o valor absoluto do número inteiro negativo é o número sem seu sinal menos.

Por exemplo, o valor absoluto de -5 é 5. O valor absoluto é indicado com barras, como segue:

| -5 | = 5

Para visualizá -lo, basta ter os espaços na linha numérica, de -5 a 0. Embora o valor absoluto de um número inteiro positivo seja o mesmo número, por exemplo | +3 | = 3, uma vez que sua distância a 0 são 3 espaços:

Pode atendê -lo: Lei de Sanduíche: Explicação e Exercícios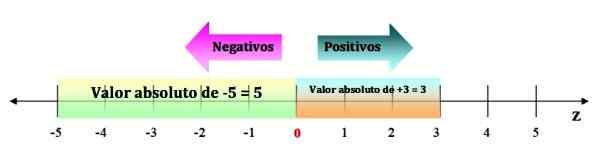Figura 3. O valor absoluto de um número inteiro é sempre uma quantidade positiva. Fonte: f. Zapata.

Propriedades

-O conjunto de números inteiros é indicado como z e inclui o conjunto de números naturais n, sendo seus elementos infinitos.

-Um número inteiro e o que se segue (ou aquele que o precede) sempre difere na unidade. Por exemplo, depois de 5 chega em 6, sendo 1 a diferença entre eles.

-Todo número inteiro tem um antecessor e um sucessor.

-Qualquer número inteiro positivo é maior que 0.

-Um número inteiro negativo é sempre menor que 0 e que qualquer número positivo. Vamos tomar, por exemplo, o número -100, isso é menor que 2, que 10 e 50. Mas também é menor que -10, -20 e -99 e é maior que -200.

-0 não tem considerações de sinal, pois não é negativo ou positivo.

-Com os números inteiros, as mesmas operações realizadas com os números naturais podem ser realizadas, a saber: soma, subtração, multiplicação, potenciação e muito mais.

-O oposto inteiro a um certo número inteiro x é -x e a soma de um número inteiro com seu oposto é 0:

x + (-x) = 0.

Operações com números inteiros

- Adição

-Se os números a serem adicionados tiverem o mesmo sinal, seus valores absolutos serão adicionados e o resultado será colocado o sinal de que os adendos têm. aqui estão alguns exemplos:

a) (+8) +( +9) = 8 +9 = +17

b) (-12) + ( - 10) = - (12 + 10) = -22

-No caso de os números terem um sinal diferente, os valores absolutos (o major do menor) são subtraídos e o resultado é colocado o sinal do número com o maior valor absoluto, como segue:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Propriedades da soma de números inteiros

-A soma é comutativa, portanto a ordem dos adiçãois não altera a soma. Seja A e B dois números inteiros, é cumprido que A+B = B+A

-0 é o elemento neutro da soma de números inteiros: a + 0 = a

-Qualquer número inteiro adicionado com seu oposto é 0. O oposto de + a é -a e, inversamente, o oposto de -a es + a. Portanto: (+ a)+ (-a) = 0.

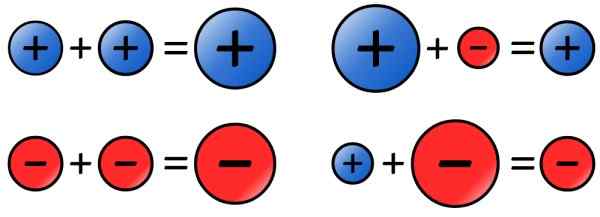Figura 4. Regra de sinais para a soma de números inteiros. Fonte: Wikimedia Commons.

- Subtração

Para subtrair números inteiros, você deve ser guiado por esta regra: A subtração é equivalente à soma de um número com seu oposto. Deixe dois números A e B, então:

A - b = a + (-b)

Por exemplo, suponha que você precise fazer a seguinte operação: (-3) - (+7), então:

(-3) -(+7) = (-3)+( -7) = -(3+7) = -10

- Multiplicação

A multiplicação de números inteiros segue certas regras para os sinais:

-O produto de dois números com O mesmo sinal É sempre positivo.

-Quando dois números se multiplicam Sinais diferentes, O resultado é sempre negativo.

Pode atendê -lo: quais são as partes da fração? (Exemplos)

-O valor do produto é igual a multiplicar os respectivos valores absolutos.

Imediatamente alguns exemplos que esclarecem o acima:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Propriedades da multiplicação de números inteiros

-A multiplicação é comutativa. Ser dois números inteiros A e B, é verdade que: a.b = b.A, que também pode ser expresso como:

A ordem dos fatores não altera o produto.

-O elemento neutro da multiplicação é 1. Ser um número inteiro, portanto.1 = 1

-Qualquer número inteiro multiplicado por 0 é igual a 0: a.0 = 0

Propriedade distributiva

A multiplicação atende à propriedade distributiva em relação à soma. Sim A, B e C são números inteiros então:

para.(B +C) = A.b + a.c

Em seguida, um exemplo de como aplicar esta propriedade:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12 -33 = 12 + (-33) = -21

Potenciação

-Se a base for positiva, o resultado da operação é sempre positivo.

-Quando a base é negativa, se o expoente for par, o resultado é positivo. E se o expoente for estranho, o resultado é negativo.

- Divisão

Na divisão, as mesmas regras de sinais se aplicam como na multiplicação:

-Ao dividir dois números inteiros do mesmo sinal, o resultado é sempre positivo.

-Quando dois números inteiros de sinais diferentes são divididos, o quociente é negativo.

Por exemplo:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Importante: A divisão não é comutativa, em outras palavras para ÷ b ≠ b ÷ a e, como sempre, a divisão entre 0 não é permitida.

- Potenciação

Seja um número inteiro e queremos aumentá -lo para um expoente n, então devemos multiplicar por si só, como mostrado abaixo:

paraⁿ = a.para.para.para.… para

Vamos também considerar o seguinte, levando em consideração que N é um número natural:

-Se A é negativo e N é par, o resultado é positivo.

-Quando A é negativo e N é estranho, resulta em um número negativo.

-Se A é positivo e N é par ou estranho, é sempre um número inteiro positivo.

-Qualquer número inteiro elevado a 0 é igual a 1: a⁰ = 1

-Cada número alto de 1 é igual ao número: A¹ = a

Vamos colocar, por exemplo, que você deseja encontrar (-3)⁴ , Para multiplicar (-3) quatro vezes por si só, assim: (-3).(-3).(-3).(-3) = 81.

Outro exemplo, também com um número inteiro negativo é:

(-2)³ = (-2).(-2).(-2) = -8

Produto de poderes básicos iguais

Suponha que dois poderes de base igual, se multiplicá -los, obtemos outro poder com a mesma base, cujo expoente é a soma dos expoentes dados:

paraⁿ ·para^m = a^{n + m}

Taxa de pó de base igual

Ao dividir os poderes da mesma base, o resultado é um poder com a mesma base, cujo expoente é a subtração dos expoentes dados:

Pode servir a você: ângulos na circunferência: tipos, propriedades, exercícios resolvidos

paraⁿ ÷ a^m = a^{n - m}

Em seguida, dois exemplos que esclarecem estes pontos:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Exemplos

Vejamos exemplos simples para aplicar essas regras, lembrando que, no caso de números inteiros positivos, o sinal pode ser dispensado:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + ( - 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) -( + 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

h) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Exercícios resolvidos

- Exercício 1

Uma formiga se move na linha numérica da Figura 1. A partir do ponto x = +3 executa os seguintes deslocamentos:

-7 unidades se movem para a direita

-Agora 5 unidades são devolvidas à esquerda

-Ande 3 unidades à esquerda.

-Ele retorna e move 4 unidades para a direita.

Em que ponto está a formiga no final da rota?

Solução

Vamos chamar os deslocamentos. Quando estão à direita, recebem um sinal positivo e quando estão no sinal negativo esquerdo. Dessa forma, e começando de x = +3 você tem:

-Primeiro D: X₁ = +3 +7 = +10

-Segundo D: X₂ = +10 +(-5) = +5

-Terceiro D: X₃ = +5 +(-3) = +2

-Quarto D: X₄ = +2 +4 = +6

Quando a formiga termina, sua caminhada está na posição x = +6. Isto é, é 6 unidades à direita de 0 na linha numérica.

- Exercício 2

Resolva a seguinte operação:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)]

Solução

Esta operação contém sinais de agrupamento, que são parênteses, colchetes e chaves. Ao resolver, você deve cuidar dos parênteses primeiro, depois dos colchetes e, finalmente, das chaves. Em outras palavras, você tem que trabalhar de dentro para fora.

Neste exercício, o ponto representa uma multiplicação, mas no caso entre um número e um parêntese ou outro símbolo, não há sentido, da mesma maneira que se entende que é um produto.

Em seguida, a resolução passo a passo, as cores servem como um guia para seguir o resultado da redução dos parênteses, que são os símbolos de grupo mais internos:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)] = =

= 36 + [- (-16)].-[-6+ 5- (0)]+ 2 (-2)] = =

= 36 + [16].-[-1] -4] =

= 52.1- 4] = 52.-3 = -156

- Exercício 3

Resolva a equação do primeiro grau:

12 + x = 30 + 3x

Solução

Os termos são agrupados com o desconhecido à esquerda da igualdade e os termos numéricos à direita:

x - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9