Método de amostragem de cotas, vantagens, desvantagens, exemplos

Ele amostragem de cotas É uma maneira não proprobabilística de obter dados de uma amostra que atribui taxas por estratos. As taxas devem ser proporcionais à fração que esse estrato representa em relação à população total e a soma das cotas deve ser igual ao tamanho da amostra. 

O pesquisador é quem decide quais serão os grupos ou estratos, por exemplo, você pode dividir uma população em homens e mulheres. Outro exemplo de estratos são as faixas etárias, por exemplo, de 18 a 25, de 26 a 40 e de 40 em diante, o que pode ser rotulado da seguinte maneira: jovens, adultos e mais velhos.

figura 1. As taxas de amostragem são segmentadas de acordo com as diferenças na população total. Fonte: Pixabay.

É muito conveniente saber anteriormente qual a porcentagem da população total representa cada estrato. Em seguida, é escolhido um tamanho de amostra que é estatisticamente significativo e cotas proporcional à porcentagem de cada estrato em relação à população total são atribuídas. A soma das taxas por estrato deve ser igual ao tamanho total da amostra.

Finalmente, os dados das cotas atribuídos a cada estrato são levados, escolhendo os primeiros elementos que completam a cota.

É precisamente por causa dessa maneira não alienadora de escolher os elementos, que esse método de amostragem é considerado não probabilístico.

[TOC]

Etapas para realizar amostragem de cotas

Passo 1

Segmentar a população total em estratos ou grupos com alguma característica comum. Esse recurso será decidido anteriormente pelo pesquisador estatístico que o estudo conduz.

Passo 2

Determine qual porcentagem em relação à população total representa cada um dos estratos ou grupos escolhidos na etapa anterior.

etapa 3

Estime um tamanho de amostra estatisticamente significativo, de acordo com os critérios e metodologias da ciência estatística.

Passo 4

Calcule o número de elementos ou cotas para cada estrato, para que sejam proporcionais à porcentagem que cada um deles representa em relação à população total e ao tamanho total da amostra.

Etapa 5

Pegue os dados dos elementos em cada estrato até concluir a cota correspondente a cada estrato.

Caso prático

Suponha que você queira saber o nível de satisfação em relação ao serviço de metrô em uma cidade. Estudos anteriores sobre uma população de 2000 pessoas determinaram que 50% dos usuários são jovens Entre 16 e 21 anos, 40% são Adultos entre 21 e 55 anos e apenas 10% dos usuários estão maior mais de 55 anos.

Aproveitar os resultados deste estudo é segmentado ou estratificado de acordo com a era dos usuários:

-Jovens: cinquenta%

-Adultos: 40%

-Maior: 10%

Como um orçamento limitado está disponível, o estudo deve ser aplicado a uma pequena amostra, mas isso é estatisticamente significativo. Um tamanho de 200 amostra é escolhido, ou seja, a pesquisa no nível de satisfação será aplicada a 200 pessoas no total.

Pode atendê -lo: Lei de Sanduíche: Explicação e Exercícios

Agora é necessário determinar a cota ou número de pesquisas para cada segmento ou estrato, que deve ser proporcional ao tamanho da amostra e à porcentagem por estrato. 

Cita de estrato

O número de número de pesquisas por estrato é assim:

Jovens: 200 * 50% = 200 * (50/100) = 100 pesquisas

Adultos: 200 * 40% = 200 * (40/100) = 80 pesquisas

Maior: 200 * 10% = 200 * (10/100) = 20 pesquisas

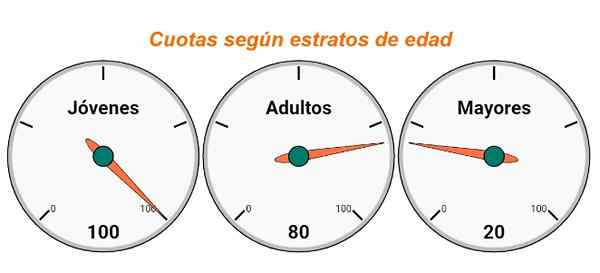Figura 2. Cotas em uma amostra de 200 indivíduos de acordo com a idade do estrato. Fonte: f. Zapata.

Observe que a soma das taxas deve ser igual ao tamanho da amostra, ou seja, igual ao número total de pesquisas que serão aplicadas. Então as pesquisas são passadas para as cotas para cada estrato.

É importante observar que esse método é muito melhor do que levar todas as pesquisas e passá -las para as primeiras 200 pessoas que aparecem, porque, de acordo com os dados anteriores, é muito provável que o estrato minoritário esteja fora do estudo.

Aplicabilidade, vantagens e desvantagens

Para que o método seja aplicável, é necessário um critério para a formação dos estratos, que depende do objetivo do estudo.

A amostragem de cotas é adequada quando você deseja conhecer as preferências, diferenças ou características dos setores para direcionar campanhas específicas de acordo com o estrato ou segmento.

Seu uso também é útil quando, por algum motivo, é interessante conhecer as características ou interesses dos setores minoritários, ou quando eles não querem ser deixados de fora do estudo.

Para ser aplicável, o peso ou o significado de cada estrato devem ser conhecidos sobre a população total. É muito importante que esse conhecimento seja confiável, caso contrário, resultados errados serão obtidos.

Vantagens

-Os tempos de estudo diminuem, porque as cotas de estrato são geralmente pequenas

-Simplifica a análise de dados.

-Minimiza os custos porque o estudo se aplica a amostras pequenas, mas bem representativas da população total.

Desvantagens

-Como os estratos são definidos a priori, é possível que certos setores da população estejam fora do estudo.

-Ao estabelecer um número limitado de estratos, é possível que os detalhes no estudo estejam sendo perdidos.

-Evitando ou incorporando como parte de outro estrato pode ser tido conclusões erradas no estudo.

-Torna impossível estimar o erro máximo de amostragem.

Aplicação simples de aplicação

Você quer fazer um estudo estatístico sobre o Nível de ansiedade Em uma população de 2000 pessoas. 

O pesquisador que direciona a pesquisa intunda que as diferenças nos resultados devem ser encontradas dependendo da idade e do sexo. É por isso que ele decide formar três estratos de idade indicados da seguinte forma: Primeiro_ead, Second_ad e Terceira idade. Em relação ao segmento sexo Os dois tipos usuais são definidos: Masculino e Fêmea.

Pode servir a você: probabilidade teórica: como divulgá -lo, exemplos, exercícios

Definido Primeiro_ead, Entre 18 e 25 anos, Second_ad aquele entre 26 e 50 anos e finalmente Terceira idade Entre 50 e 80 anos.

Analisar os dados da população total precisa: 

45% da população pertence ao Primeiro_ead.

40% está no Second_ad.

Finalmente, apenas 15% da população em estudo pertence ao Terceira idade.

Usando uma metodologia adequada, que não é detalhada aqui, é determinado que uma amostra de 300 pessoas é estatisticamente significativa.

Determinação de cotas por idade

O próximo passo será encontrar as cotas correspondentes pelo segmento Idade, O que é feito da seguinte maneira:

First_eity: 300 * 45% = 300 * 45 /100 = 135

Second_ad: 300 * 40% = 300 * 40/1 = 120

Terceiro_ad: 300 * 15% = 300 * 15 /100 = 45

É verificado que a soma das cotas dá o tamanho total da amostra.

Determinação de cotas por idade e sexo

Até agora, o segmento não foi levado em consideração sexo Da população, dois estratos já foram definidos neste segmento: Fêmea e Masculino. Novamente, você deve analisar os dados da população total, que mostram as seguintes informações: 

-60% da população total é sexo Fêmea.

-Enquanto isso, 40% da população a ser estudada pertence ao sexo Masculino.

É importante observar que as porcentagens anteriores em relação à distribuição da população de acordo com o sexo, não levam em consideração a idade. 

Em vista de que não há mais informações disponíveis, a suposição será feita de que essas proporções em termos de sexo são igualmente distribuídas nos 3 estratos de Idade que foram definidos para este estudo. Com essas considerações, agora continuamos estabelecendo as cotas por idade e sexo, o que significa que agora haverá 6 sub-estados:

S1 = First_AD e Feminino: 135 * 60% = 135 * 60 /100 = 81

S2 = primeiro e homem: 135 * 40% = 135 * 40 /100 = 54

S3 = Segundo e Feminino: 120 * 60% = 120 * 60 /100 = 72

S4 = segundo e masculino: 120 * 40% = 120 * 40 /100 = 48

S5 = terceiro _tad e fêmea: 45 * 60% = 45 * 60 /100 = 27

S6 = terceiro _dad e masculino: 45 * 40% = 45 * 40 /100 = 18

Aplicação de pesquisa e estudo dos resultados

Uma vez que o segmento seis (6).

As pesquisas serão aplicadas da seguinte forma, 81 pesquisas são realizadas e as 81 primeiras pessoas que estão no segmento são entrevistadas S1. Então é feito da mesma maneira com os cinco segmentos restantes.

Pode atendê -lo: quais são os elementos de um ângulo?

A sequência do estudo é a seguinte:

-Analise os resultados da pesquisa, que são discutidos, analisando os resultados por segmento.

-Fazer comparações entre os resultados do segmento.

-Finalmente elaborados hipóteses que explicam as causas desses resultados.

Diferença com amostragem aleatória estratificada

Em nosso exemplo em que aplicamos a amostragem de cotas, a primeira coisa que é feita é estabelecer as taxas e depois realizar o estudo. Obviamente, essas cotas não são totalmente caprichosas, porque foram baseadas em informações estatísticas anteriores sobre a população total.

No caso de não ter informações anteriores sobre a população em estudo, é uma forma aleatória preferível.

Uma maneira de garantir a aleatoriedade seria usar um gerador de números aleatórios e pesquisar funcionários cujo número de funcionários coincide com o do gerador aleatório.

Depois de ter os dados e, como o objetivo do estudo é ver os níveis de ansiedade de acordo com os estratos de idade e sexo, os dados são separados de acordo com as seis categorias que definimos anteriormente. Mas sem estabelecer nenhuma taxa anterior.

É por esse motivo que o método de Amostragem aleatória estratificada É considerado um método probabilístico. Enquanto isso, ele amostragem de cotas anteriormente estabelecido no. 

No entanto, se as cotas forem estabelecidas com informações com base nas estatísticas da população, pode -se dizer que o método de amostragem de cotas É aproximadamente probabilístico.

Exercício proposto

O exercício a seguir é proposto:

Em uma faculdade de ensino médio, uma pesquisa sobre a preferência entre estudar ciências ou estudar humanidades. 

Suponha que a escola tenha um total de 1000 estudantes agrupados em cinco níveis, de acordo com o ano de estudo. Sabe -se que existem 350 alunos no primeiro ano, 300 em segundo, 200 em terceiro, 100 em quarto e finalmente 50 no quinto ano. Sabe -se também que 55% dos alunos são meninos e 45% são meninas.

Determine estratos e taxas por estrato, para saber o número de pesquisas para aplicar a participação nos segmentos do ano de estudo e sexo. Suponha também que a amostra será 10% da população total de estudantes.

Referências

1. Berenson, m. 1985.Estatísticas para administração e economia, conceitos e aplicações. Editorial inter -americano.
2. Estatisticas. Amostragem de cotas. Recuperado de: Encyclopediaeconomica.com.
3. Estatisticas. Amostragem. Recuperado de: estatísticas.Esteira.USON.mx.
4. Explorável. Amostragem de cotas. Recuperado de: explorável.com.
5. Moore, d. 2005. Estatísticas básicas aplicadas. 2º. Edição.
6. NetQuest. Amostragem probabilística: amostragem estratificada. Recuperado de: netQuest.com.
7. Wikipedia. Amostra estatística. Recuperado de: em.Wikipedia.org