Medidas de variabilidade

figura 1.- As medidas de variabilidade mais conhecidas. Fonte: f. Zapata.

O que são medidas de variabilidade?

As Medidas de variabilidade, Também chamados de medidas de dispersão, são indicadores estatísticos que indicam o quão próximo ou remoto os dados de sua média aritmética são encontrados. Se os dados estiverem próximos da média, a distribuição está concentrada e, se estiverem longe, é então uma distribuição dispersa.

Existem muitas medidas de variabilidade, entre as mais conhecidas são:

• Faixa
• Desvio médio
• Variação
• Desvio padrão

Essas medidas complementam as medidas de tendência central e são necessárias para entender a distribuição dos dados obtidos e extrair o máximo de informações possível.

Faixa

O intervalo ou rota mede a amplitude de um conjunto de dados. Para determinar seu valor, a diferença entre o valor mais alto x é encontrada_máx e o menor valor X_min:

R = x_máx - x_min

Se os dados não estiverem soltos, mas agrupados por intervalo, o intervalo será calculado pela diferença entre o limite superior do último intervalo e o limite inferior do primeiro intervalo.

Quando o intervalo é um valor pequeno, significa que todos os dados estão bem próximos um do outro, mas uma grande variedade indica que há muita variabilidade. É evidente que, além do limite superior e do limite inferior dos dados, o intervalo não leva em consideração os valores entre eles; portanto, não é aconselhável usá -lo quando o número de dados é grande.

No entanto, é uma medida imediata para calcular e possui as mesmas unidades de dados, por isso é fácil interpretá -lo.

Exemplo de classificação

Em seguida, a lista está disponível com o número de metas marcadas durante o fim de semana, nas ligas de futebol de nove países:

Pode atendê -lo: quais são os divisores de 30? (Explicação)

40, 32, 35, 36, 37, 31, 37, 29, 39

É um conjunto de dados sem agrupar. Para encontrar o intervalo, eles passam a ordená -los de menos para maiores:

29, 31, 32, 35, 36, 37, 37, 39, 40

Os dados com o valor mais alto são 40 objetivos e o valor mais baixo é de 29 objetivos, portanto, o intervalo é:

R = 40−29 = 11 gols.

Pode -se considerar que o intervalo é pequeno em comparação com os dados mínimos de valor, o que é de 29 objetivos, por isso pode ser assumido que os dados não têm grande variabilidade.

Desvio médio

Essa medida de variabilidade é calculada através da média dos valores absolutos dos desvios em relação à média. Denotando o desvio médio como D_M, Para dados não agrupados, o desvio médio é calculado pela seguinte fórmula:

Onde n é o número de dados disponíveis, x_Yo Representa cada dados e x̄ é a média, o que é determinado adicionando todos os dados e dividindo -se entre n:

O desvio médio permite saber, em média, quantas unidades os dados se desviam da média aritmética e têm a vantagem de ter as mesmas unidades que os dados com os quais funciona.

Exemplo de desvio médio

De acordo com os dados do intervalo, o número de metas marcadas é:

40, 32, 35, 36, 37, 31, 37, 29, 39

Se você quiser encontrar o desvio médio D_M Desses dados, é necessário calcular primeiro a média aritmética x̄:

E agora que o valor de x̄ é conhecido, passamos a encontrar o desvio médio_M:

= 2.99 ≈ 3 gols

Portanto, pode -se dizer que, em média, os dados se afastam aproximadamente em 3 objetivos médios que são 35 gols e, como observado, é uma medida muito mais precisa do que o intervalo.

Pode atendê -lo: Hiperbola

Variação

O desvio médio é uma medida de variabilidade muito mais fina que o intervalo, mas calculado pelo valor absoluto das diferenças entre cada dados e a média, ele não oferece maior versatilidade do ponto de vista algébrico.

Portanto, a variação é preferida, que corresponde à média da diferença quadrática de cada dados com a média e é calculada usando a fórmula:

Nesta expressão, S² indica a variação e, como sempre, x_Yo representa cada um dos dados, x̄ é a média e n os dados totais.

Ao trabalhar com uma amostra em vez da população, é preferido calcular a variação como esta:

A diferença com a fórmula anterior é que, no denominador, existem n - 1 em vez de n. Acontece que, dividindo -se por n, a variação da amostra subestima a variação da população da qual foi extraída, mas não quando é dividida por n - 1. Em alguns textos que a expressão aparece com o nome de Quasi-Variza.

De qualquer forma, a variação é caracterizada por ser sempre uma quantidade positiva, mas sendo a média das diferenças quadráticas, é importante observar que não possui as mesmas unidades que as dos dados.

Exemplo de variação

Para calcular a variação dos dados dos exemplos de intervalo e desvio médio, os valores correspondentes são substituídos e a soma indicada. Nesse caso, é escolhido dividir entre N-1:

= 13.86

Desvio padrão

A variação não possui a mesma unidade que a variável em estudo, por exemplo, se os dados vieram em metros, a variação resultará em metros quadrados. Ou no exemplo dos objetivos que estaria em objetivos quadrados, o que não faz sentido.

Pode atendê -lo: quais são os elementos da parábola? (Peças)

Portanto, o desvio padrão é definido, também chamado desvio típico, Como a raiz quadrada da variação:

S = √s²

Dessa maneira.

Tanto a variação quanto o desvio padrão são as medidas de variabilidade a serem escolhidas quando a média aritmética é a medida da tendência central que melhor descreve o comportamento dos dados.

E é que o desvio padrão tem uma propriedade importante, conhecida como Teorema de Chebyshev: pelo menos 75% das observações estão no intervalo definido por x̄ ± 2s. Em outras palavras, 75% dos dados estão, no máximo, a uma distância igual a 2s em torno da média.

Da mesma forma, pelo menos 89% dos valores estão a uma distância de 3s da média, uma porcentagem que pode ser expandida, desde que muitos dados estejam disponíveis e que sigam uma distribuição normal.

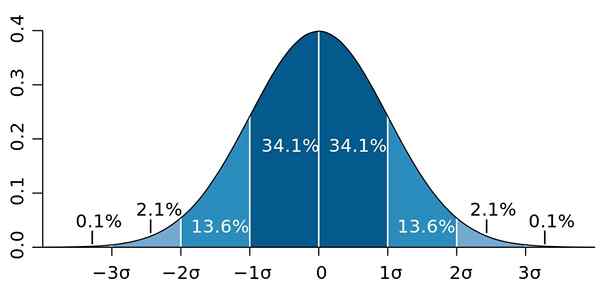
Figura 2.- Se os dados seguirem uma distribuição normal, 95.4 deles são dois desvios padrão em ambos os lados da média. Fonte: Wikimedia Commons.

Exemplo de desvio padrão

O desvio padrão dos dados apresentados nos exemplos anteriores é:

S = √s² = √13.86 = 3.7 ≈ 4 gols