Distribuição F Características e exercícios resolvidos

O distribuição f o Fisher-Snedecor Distribuição é o que é usado para comparar as variações de duas populações diferentes ou independentes, cada uma das quais segue uma distribuição normal.

A distribuição que segue a variação de um conjunto de amostras de uma única população normal é a distribuição ji-quadrado (Χ²) do grau n-1, se cada uma das amostras do conjunto tiver n elementos.

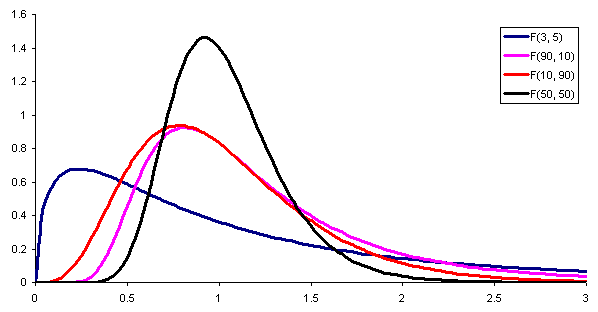
figura 1. Aqui está a densidade de probabilidade da distribuição F com diferentes combinações de parâmetros (ou graus de liberdade) de numerador e denominador, respectivamente. Fonte: Wikimedia Commons.

Para comparar as variações de duas populações diferentes, é necessário definir um Estatística, Ou seja, uma variável aleatória auxiliar que permite discernir se ambas as populações têm ou não a mesma variação.

Essa variável auxiliar pode ser diretamente o quociente das variações de amostra de cada população; nesse caso, se o quociente estiver próximo da unidade, é evidenciado que ambas as populações têm variações semelhantes.

[TOC]

A estatística F e sua distribuição teórica

A variável aleatória f ou estatística F proposta por Ronald Fisher (1890 - 1962) é a usada com mais frequência para comparar as variações de duas populações e é definida da seguinte maneira:

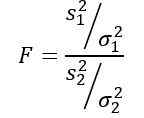
Sendo s² A variação da amostra e σ² A variação da população. Para distinguir cada um dos dois grupos populacionais, as assinaturas 1 e 2 são usadas, respectivamente.

Sabe-se que a distribuição ji-quadrado com (n-1) de liberdade é a que segue a variável auxiliar (ou estatística) que é definida abaixo:

X² = (N-1) s² / σ².

Portanto, a estatística F segue uma distribuição teórica dada pela seguinte fórmula:

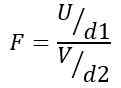
Ser OU A distribuição ji-quadrado com D1 = n1 - 1 graus de liberdade para a população 1 e V A distribuição ji-quadrado com D2 = n2 - 1 graus de liberdade para a população 2.

Pode servir você: álgebra vetorial

A proporção definida dessa maneira é uma nova distribuição de probabilidade, conhecida como distribuição f com D1 graus de liberdade no numerador e D2 graus de liberdade no denominador.

Média, moda e variação de distribuição f

Metade

A distribuição média f é calculada da seguinte forma:

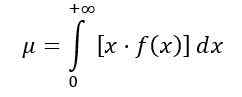
Sendo f (x) a densidade de probabilidade de distribuição F, que é mostrada na Figura 1 para várias combinações de parâmetros ou graus de liberdade.

Você pode escrever a densidade de probabilidade f (x), dependendo da função γ (função gama):

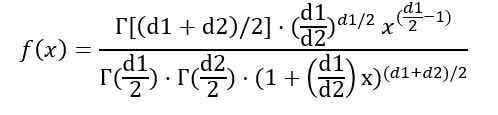
Uma vez que a integral indicou anteriormente, conclui -se que a média da distribuição f com graus de liberdade (D1, D2) é: IS: IS: IS: IS:

μ = d2 / (d2 - 2) com d2> 2

Onde mostra que, curiosamente, a média não depende dos graus de liberdade D1 do numerador.

Moda

Por outro lado, a moda depende de D1 e D2 e ​​é dada por:

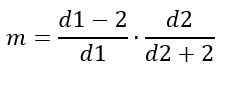
Para D1> 2.

Variação da distribuição f

A variação σ² da distribuição f é calculada a partir da integral:

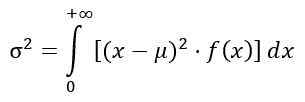
Obtenção:

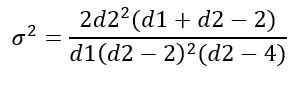
Gerenciamento de distribuição f

Como outras distribuições contínuas de probabilidade que envolvem funções complicadas, a distribuição f gerenciamento é feita por tabelas ou por software.

Tabelas de distribuição f

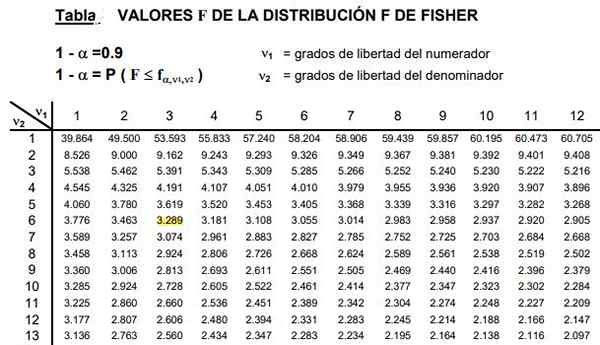Figura 2. Uma parte da tabela de distribuição F é mostrada, que geralmente é muito extensa porque há uma ampla combinação de possíveis graus de liberdade D1 e D2.

As tabelas envolvem os dois parâmetros ou graus de liberdade de distribuição F, a coluna indica o grau de liberdade do numerador e a fila o grau de liberdade do denominador.

Pode atendê -lo: desigualdade do triângulo: demonstração, exemplos, exercícios resolvidos

A Figura 2 mostra uma seção da tabela de distribuição F para o caso de um Nível de significância 10%, ou seja, α = 0,1. O valor de f é destacado quando d1 = 3 e d2 = 6 com nível de confiança 1- α = 0,9 que é 90%.

Software para distribuição F

Quanto ao software que gerencia a distribuição f, há uma grande variedade, das planilhas como Excel até pacotes especializados como Minitab, SPSS e R Para citar alguns dos mais conhecidos.

Deve -se notar que o software de geometria e matemática Geogebra Possui uma ferramenta estatística que inclui as principais distribuições, incluindo distribuição F. A Figura 3 mostra a distribuição f para o caso d1 = 3 e d2 = 6 nível de confiança 90%.

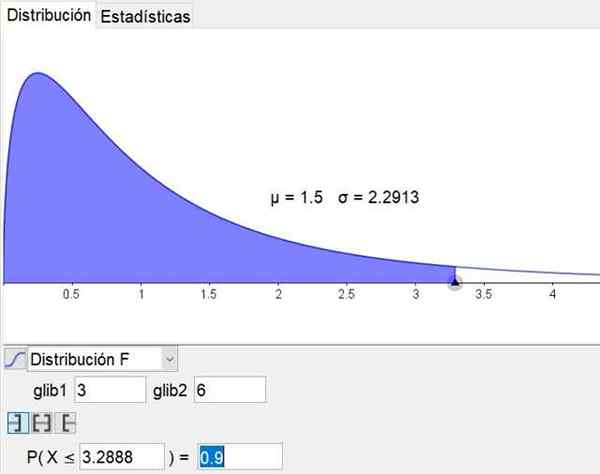Figura 3. A distribuição F é mostrada para o caso d1 = 3 e d2 = 6 com nível de confiança de 90%, obtido através da ferramenta estatística geogebra. Fonte: Geogebra.org

Exercícios resolvidos

Exercício 1

Considere duas amostras de populações que têm a mesma variação populacional. Se a amostra 1 é o tamanho n1 = 5 e a amostra 2 é o tamanho n2 = 10, determine a probabilidade teórica de que a razão de suas respectivas variações seja menor ou igual a 2.

Solução

Deve -se lembrar que a estatística f é definida como:

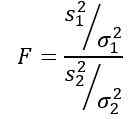
Mas somos informados de que as variações populacionais são as mesmas, portanto, para este exercício, ele se aplica:

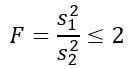
Como você deseja saber a probabilidade teórica de que essa proporção de variações de amostra seja menor ou igual a 2, precisamos conhecer a área sob a distribuição F entre 0 e 2, que pode ser obtida por tabelas ou software. Para isso, deve -se levar em consideração que a distribuição necessária f tenha d1 = n1 - 1 = 5 - 1 = 4 e d2 = n2 - 1 = 10 - 1 = 9, isto é, a distribuição f com graus de liberdade (4, 9).

Pode servir a você: série de poder: exemplos e exercícios

Usando a ferramenta estatística de Geogebra Foi determinado que esta área é 0.82, conclui -se que a probabilidade de que a proporção de variações de amostra seja menor ou igual a 2 é 82%.

Exercício 2

Existem dois processos de fabricação de folhas finas. A variabilidade da espessura deve ser o máximo possível. 21 amostras de cada processo são coletadas. A amostra de processo tem um desvio padrão de 1,96 microns, enquanto o do processo B tem desvio padrão de 2,13 mícrons. Qual dos processos tem menor variabilidade? Use um nível de rejeição de 5%.

Solução

Os dados são os seguintes: SB = 2,13 com NB = 21; SA = 1,96 com Na = 21. Isso significa que você precisa trabalhar com uma distribuição F de (20, 20) graus de liberdade.

A hipótese nula implica que a variação populacional de ambos os processos é idêntica, ou seja, σa^2 / σb^2 = 1. A hipótese alternativa implicaria diferentes variações populacionais.

Então, sob a suposição de variações populacionais idênticas, a estatística f calculada como: fc = (sb/sa)^2 é definida.

Como o nível de rejeição foi tomado como α = 0,05, então α/2 = 0,025

A distribuição F (0.025; 20,20) = 0,406, enquanto F (0.975; 20,20) = 2,46.

Portanto, a hipótese nula será verdadeira se o F calculado cumprir: 0,406≤fc≤2,46. Caso contrário, a hipótese nula é rejeitada.

Como Fc = (2,13/1,96)^2 = 1,18 conclui -se que a estatística da FC está na faixa de aceitação da hipótese nula com uma certeza de 95%. Em outras palavras, com uma certeza de 95%, ambos os processos de fabricação têm a mesma variação populacional.

Referências

1. F Teste de Independência. Recuperado de: SaylordOtorg.Github.Io.
2. Onda médica. Estatísticas aplicadas às ciências da saúde: teste f. Recuperado de: medwave.Cl.
3. Probabilidades e estatísticas. Distribuição f. Recuperado de: Probabilidades Andestics.com.
4. TRIOLA, m. 2012. Estatísticas elementares. 11º. Edição. Addison Wesley.
5. Unam. Distribuição f. Recuperado de: Advisory.Cuautitlan2.Unam.mx.
6. Wikipedia. Distribuição f. Recuperado de: é.Wikipedia.com