Lei de Fick

Qual é a lei de Fick?

O Lei de Fick É uma equação matemática que relaciona o fluxo de massa divulgado em um meio com o gradiente de concentrações ou pressões. Foi formulado em 1855 pelo fisiologista alemão e pelo doutor Adolf Fick, que inspirado pelas leis de Fourier (condução térmica) e ohm (condução elétrica), modelou o processo de difusão de oxigênio aos alvéolos dos pulmões.

A lei de Fick apresenta a particularidade de que não é apenas aplicável a fenômenos de difusão química ou bioquímica, mas àqueles de qualquer tipo de natureza. Portanto, serve para modelar a disseminação de átomos entre sólidos, sendo muito útil na física de materiais e engenharia.

Representação de um processo de difusão através de uma membrana semipermeável. Fonte: Gabriel Bolívar.

No entanto, a base central é a mesma para quase todos os fenômenos de difusão, que são ilustrados acima. Partículas roxas, átomos ou moléculas, estão espalhadas por uma membrana espessa semipermeável L e área transversal para. À esquerda, temos uma concentração maior C₁ de partículas que à direita, C₂.

A lei de Fick estabelece o seguinte: O fluxo de massa que é disseminado através de uma superfície é proporcional ao gradiente de concentração (c₂-C₁/L) e uma constante d chamada de difusão ou coeficiente de difusividade.

Esta lei tem duas formas: uma baseada no espaço (x) e outra, dependendo do espaço e do tempo (x, t). O primeiro se aplica a sistemas em condições estacionárias, enquanto o segundo para sistemas real e não estacionários.

Primeira Lei de Fick

Componentes e equação

O l grosso L da membrana semipermeável representa a distância (x) que as partículas devem viajar para alcançar o outro lado. Como pode ser visto na imagem, partículas roxas, mais elas se afastam do compartimento esquerdo, onde C₁ É ótimo, sua concentração diminui para o valor de C₂. Isto é, a concentração muda ao longo da espessura da membrana, sendo dependente de x.

Essa variação de concentração dependendo da distância é o que é conhecido como gradiente de concentração: (c₂-C₁)/L O (C₂-C₁)/x. Observe que seu valor é negativo (-1), porque C₂ > C₁.

Por outro lado, também temos a velocidade com que as partículas estão espalhadas pela membrana ou pelo espaço em questão. Essa velocidade depende do tamanho e massa das partículas, bem como da natureza do meio ambiente e temperatura. O coeficiente de difusão D representa essa velocidade e pode ser constante ou não durante a difusão.

Pode atendê -lo: filtro de laboratório): características, funções, tipos

E, finalmente, temos um fluxo de massa 'J' que atravessa a área transversal da membrana ou o canal onde as partículas se espalham. Agrupando estes termos, nasce a equação da primeira lei de Fick:

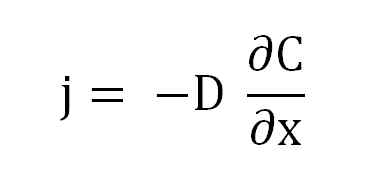Equação da primeira lei de Fick. Fonte: Gabriel Bolívar.

Onde j é proporcional a d e a (∂c/∂x), o gradiente de concentração.

Interpretação e unidades

O símbolo negativo na equação serve para neutralizar o sinal negativo do gradiente de concentrações. Caso contrário, J teria um valor negativo, que não. Da mesma forma, o valor de D é positivo, de modo que, multiplicando pelo sinal negativo que o precede, fornece um valor negativo.

A primeira lei de Fick indica o seguinte: quanto maior o gradiente de concentração (∂c/∂x), maior o fluxo de massa j. Isto é, a diferença entre c₂ e C₁ Torna -se maior e, portanto, mais partículas se espalharão pela membrana.

Por outro lado, J também depende de D, que por sua vez depende de parâmetros como temperatura, viscosidade, peso molecular e área transversal para:

D ∝ (a/l) (s/√m_C)

Onde s é a solubilidade da partícula que se espalha com o meio ambiente, e m_C Seu peso molecular.

Em relação às unidades dos componentes ou termos da equação que temos:

-C (kg · m^-3 ou mol · m^-3)

-D (m^-2· S^-1)

-J (kg · m^-2· S^-1 ou mol · m^-2· S^-1)

Deslocamento quadrático médio líquido

Durante a disseminação, as partículas colidem entre si e, após curtos intervalos de tempo, acabam viajando enormes distâncias Δx. No entanto, dependendo do significado desses deslocamentos, Δx pode ter valores negativos ou positivos (de acordo com um ponto de origem). É por isso que a média dos valores Δx para todas as moléculas tende a 0.

Por outro lado, os valores de Δx são muito pequenos em comparação com as distâncias que executam as partículas. Quando colidem, perdem a mobilidade em direção a uma direção, consequentemente com um deslocamento líquido limitado; Por exemplo, 2 cm de adiantamento em uma direção depois de viajar centenas de metros em colisões e rebotes.

Einstein, em 1905, encontrou uma expressão matemática para o pergaminho médio do deslocamento (portanto, diferente de 0):

<(Δx)²> = 2dt

Definindo

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_Rms É o deslocamento quadrático líquido médio das partículas em questão. (Δx)_Rms Ele nos diz quanta partículas se move em média (em uma direção positiva ou negativa) de acordo com o tempo. Algumas partículas se moverão mais distâncias mais próximas do que (Δx)_Rms, causando uma distribuição gaussiana.

Pode atendê -lo: óxido de cálcio (CAO)

Fick Segunda Lei

Equação

A primeira lei de Fick descreve a difusão em condições estacionárias, ou seja, o fluxo de massa J não varia com o tempo. Em sistemas reais, no entanto, temos condições não estacionárias, onde o fluxo de massa não apenas varia no espaço, mas também com o tempo. Portanto, está interessado em determinar (∂c/∂t).

Abaixo, temos duas equações que representam a segunda lei de Fick:

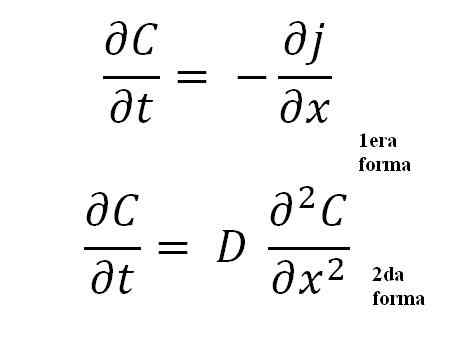Equações da segunda lei de Fick. Fonte: Gabriel Bolívar.

A segunda forma é a mais importante de todas, pois representa a equação matemática geral para qualquer processo de disseminação; Térmico, elétrico, atômico, etc.

Dedução

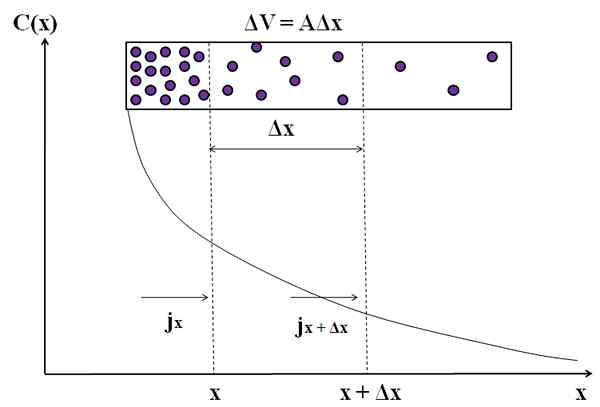Representação gráfica de como o fluxo de massa não é constante na disseminação dessas moléculas. Fonte: Gabriel Bolívar.

Considere novamente partículas roxas em uma câmara retangular. Entre as distâncias x e x+Δx, temos um fluxo j_x (recebimento) e j_x+Δx (extrovertido). O volume da câmera entre essas distâncias é definido por:

ΔV = AΔX

Observe que o gráfico c (x) vs x não origina uma linha reta, por isso temos valores diferentes de j (j (j_x ≠ j_x+Δx). Devemos determinar ΔC/ΔT.

A massa m_x Será igual a:

m_x = J_x AΔT

Uma análise dimensional ajuda a entender o porquê:

kg = (kg · m^-2· S^-1) (m²(S) (s)

Da mesma maneira que calculamos m_x+Δx:

m_{x+ Δx} = J_x+Δx AΔT

Sendo a massa que se acumula nessa região igual a Δm:

Δm = m_x - m_{x+ Δx}

= (j_x - J_{x+ Δx}) AΔT

= -(J_{x+ Δx} - J_x) AΔT

= -ΔJAΔT

E sabendo que ΔC = ΔM/ΔV

ΔC = -ΔJAΔT/ ΔV

= -ΔJAΔT /AΔX

= -ΔJΔT/ΔX

Nós limpamos ΔC/ΔT

ΔC/ΔT = -ΔJ/ΔX

Esta expressão indica que a variação da concentração ao longo do tempo é igual à variação do fluxo j em relação ao seu deslocamento. Aplicando os limites para Δt e Δx tendendo a 0, obtemos a mesma expressão que um derivado parcial:

∂c/∂t = -(∂j/∂x) (1º formulário)

Finalmente, o segundo formulário é obtido substituindo J pela primeira lei de Fick:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (2º formulário)

Exercícios resolvidos

Nos exercícios a seguir, sistemas muito simples serão considerados cujas incógnitas podem ser resolvidas usando a primeira lei de Fick.

Exercício 1

Declaração

Em um cano de 15 metros de comprimento e 21 centímetros de largura, e que também é saturado com nitrogênio, uma corrente de oxigênio é espalhada de uma extremidade para outra a uma temperatura de 0 ºC. Sabendo que a pressão no lado esquerdo (P₁) é 20 kg/m³, E que a pressão no lado direito (P₂) é 10 kg, determine:

Pode atendê -lo: Hydronio Ion

a) o fluxo de massa que está espalhado

b) Quantos quilos de ou₂ Eles se espalharão pelo cano em 17 minutos?

c) o gradiente de concentração ou pressões

d) a pressão de O₂ A uma distância de 7 metros da entrada do pipeline

e) quanto será 80 kg de O₂ Ao se espalhar através deste tubo?

Considere que d_O2-N2 é igual a 1.8 · 10^-5 m²· S^-1.

Resolução

Da primeira lei de Fick, temos que resolver a subseção a):

J = -d (P₂-P₁)/EU

= -(1.8 · 10^-5 m²· S^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

Para b) precisamos da área do tubo:

A = π (0.21 m)²

= 0.14 m²

E multiplicamos J por A e tempo t para determinar a massa de ou₂ Dificuldade:

m_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Agora, para a subseção c) temos que o gradiente é igual a:

Gradiente = (P₂-P₁)/EU

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Mas assumimos o valor positivo, o que faz sentido físico:

2/3 (kg/m³) · M^-1

Esse valor nos servirá para resolver a subseção d) se o gradiente for bem interpretado: cada medidor a pressão de ou₂ 2/3 kg/m cairá³. Ao espalhar 7 metros, teremos:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 ou 4.7 kg/m³

Isto é, a pressão a essa distância será:

(20-4.7) (kg/m³) = 15.3 kg/m³

E, finalmente, a subseção e) é semelhante a b), apenas que agora limpamos o tempo e não a massa:

m_O2 = Jat

t = m_O2/JA

= (80 kg)/(1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²)

= 47619.04 s ou 0.55 dias

Exercício 2

Declaração

Determinar (Δx)_Rms Para sacarose em água em t = 1 min, 1 h e 1 dia. O coeficiente de disseminação de sacarose na água é 0.52 · 10^-5cm²· S^-1.

Resolução

Aplicamos a equação:

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

Avaliamos (Δx)_Rms Com os tempos expressos em segundos. Para t = 1 min ou 60 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (anos 60))^1/2

= 0.025 cm

Para t = 1 h ou 3600 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (3600s))^1/2

= 0.19 cm

E finalmente para t = 1 dia ou 86400 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (86400s))^1/2

= 0.95 cm

Observe que, com o passar do tempo, as moléculas de sacarose nem sequer foram capazes de mover 1 cm em nenhuma direção.

Referências

1. Walter J. Moore. (1963). Química Física. Em cinética química. Quarta edição, Longmans.
2. Irã. Levine. (2009). Princípios da físico -química. Sexta edição. Mc Graw Hill.
3. Introdução à ciência e engenharia de materiais. (11 de março de 2018). Segunda Lei de Fick. Prof. Rajesh Prasad. [VÍDEO]. Recuperado de: youtube.com
4. Wikipedia. (2020). Leis de difusão de Fick. Recuperado de: em.Wikipedia.org
5. Laura Dickson. (10 de setembro de 2020). DIFUSÃO. Química Librettexts. Recuperado de: química.Librettexts.org
6. Larissa Zhou et al. (1 de setembro de 2015). Entendendo a teoria da difusão e a lei de Fick através da comida e culinária. A Sociedade Fisiológica Americana. doi.org/10.1152/Advan.00133.2014