Fórmula de interferência destrutiva e equações, exemplos, exercícios

O Interferência destrutiva, Na física, ocorre quando duas ondas independentes que se combinam na mesma região do espaço estão desatualizadas. Então os cumes de uma das ondas encontram os vales do outro e o resultado é uma onda com uma amplitude nula.

Várias ondas passam sem problemas pelo mesmo ponto no espaço e, em seguida, cada uma segue seu caminho sem ser afetado, como as ondas na água da figura a seguir:

figura 1. Gotas de chuva produzem ondas na superfície da água. Quando as ondas resultantes têm zero largura, diz -se que a interferência é destrutiva. Fonte: Pixabay.

Suponha que duas ondas de igual amplitude e frequência ω, que chamaremos e₁ e e₂, que pode ser descrito matematicamente através das equações:

e₁= Um sen (kx -ω)

e₂ = Um sen (kx -ωt + φ)

A segunda onda e₂ Tem uma lacuna φ em relação ao primeiro. Quando combinados, como as ondas podem ser sobrepostas sem problemas, elas dão origem a uma onda resultante chamada e_R:

e_R = y₁ + e₂ = Um sen (kx -ω) + um sin (kx -ωt + φ)

Através da identidade trigonométrica:

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

A equação para e_R Ele se transforma em:

e_R = [2a cos (φ/2)] sin (kx - ωt + φ/2)

Agora, esta nova onda tem uma amplitude resultante para_R = 2a cos (φ/2), que depende da diferença de fase. Quando essa diferença de fase adquire os valores+π ou -π, a amplitude resultante é:

PARA_R = 2a cos (± π/2) = 0

Desde cos (± π/2) = 0. Precisamente então é quando a interferência destrutiva entre as ondas ocorre. Em geral, se o argumento do cosseno for da forma ± kπ/2 com k ímpares, a amplitude para_R  É 0.

[TOC]

Exemplos de interferência destrutiva

Como vimos, quando duas ou mais ondas passam ao mesmo tempo em um ponto, elas se sobrepõem, dando origem a uma onda resultante cuja amplitude depende da diferença de fase entre os participantes.

Pode servir a você: Variação linear: conceito, exemplos, exercício resolvido

A onda resultante tem a mesma frequência e número de ondas que as ondas originais. Na animação seguinte, duas ondas são sobrepostas em cores azuis e verdes. A onda resultante está em vermelho.

A amplitude cresce quando a interferência é construtiva, mas é cancelada quando é destrutiva.

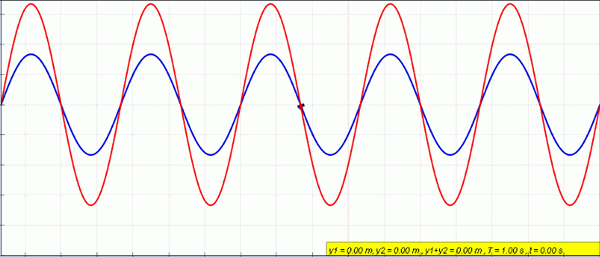Figura 2. Ondas de cor azul e verde se sobrepõem para dar origem à onda vermelha. Fonte: Wikimedia Commons.

As ondas que têm a mesma amplitude e frequência são chamadas ondas coerentes, contanto que eles mantenham entre eles a mesma diferença de fase φ. Um exemplo de onda coerente é a luz do laser.

Condição para interferência destrutiva

Quando as ondas azuis e verdes estão desatualizadas em 180 º em um determinado ponto (veja a Figura 2), isso significa que, enquanto se movem, eles têm diferenças de fase φ de π radianes, 3π radianos, 5π radianos e assim por diante.

Dessa maneira, dividindo o argumento da amplitude resultante em 2, resulta em radianos (π/2), (3π/2) radianos ... e o cosseno de tais ângulos é sempre 0. Portanto, a interferência é destrutiva e a amplitude é feita 0.

Interferência de ondas destrutivas na água

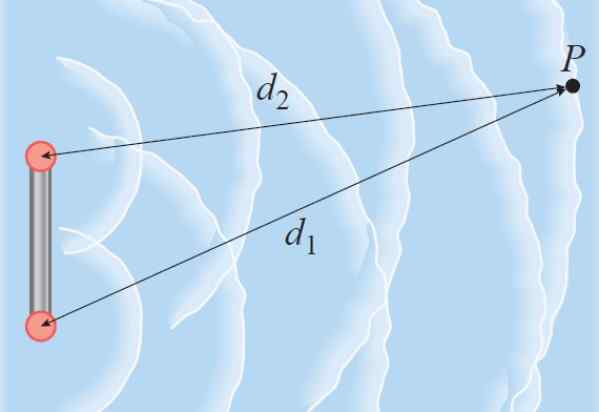
Suponha que duas ondas coerentes comecem em uma entre si. Essas ondas podem ser aquelas que se espalham pela água graças a duas barras que vibram. Se as duas ondas viajarem para o mesmo ponto P, percorrendo diferentes distâncias, a diferença de fase é proporcional à diferença de caminho.

Figura 3. As ondas produzidas pelas duas fontes viajam na água até o ponto P. Fonte: Giambattista, A. Física.

Como um comprimento de onda λ é igual a uma diferença de 2π radianos, é verdade que:

│d₁ - d₂│ / λ = diferença de fase / 2π radianos

Diferença de fase = 2π x│d₁ - d₂│/ λ

Pode servir a você: Polarização da luz: tipos, exemplos, aplicações

Se o caminho das estradas é um número ímpar de onda semi-onda, ou seja: λ/2, 3λ/2, 5λ/2 e assim por diante, então a interferência é destrutiva.

Mas se a diferença da estrada for um número de torque de comprimentos de onda, a interferência é construtiva e as amplitudes são adicionadas no ponto P.

Interferência destrutiva de ondas luminosas

As ondas leves também podem interferir entre si, como afirmado por Thomas Young em 1801 através de seu célebre experimento de fenda dupla dupla.

Young deu luz através de uma fenda feita em uma tela opaca, que, de acordo com o princípio de Huygens, por sua vez gera duas fontes de luz secundárias. Essas fontes continuaram a caminho de uma segunda tela opaca com duas fendas e a luz resultante foi projetada em uma parede.

O diagrama é observado na imagem a seguir:

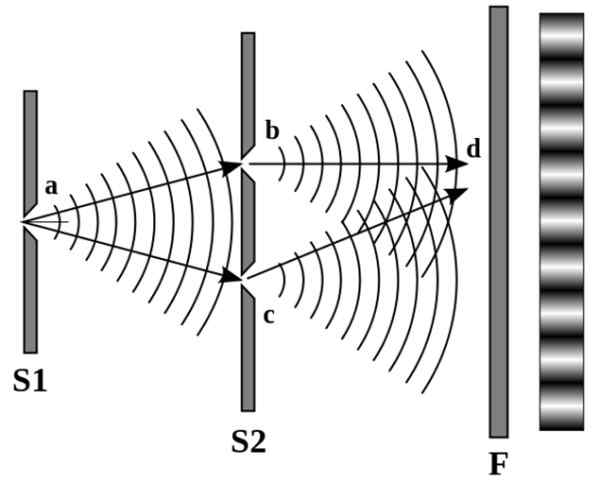Figura 4. O padrão de linhas claras e escuras na parede direita é devido a interferência construtiva e destrutiva, respectivamente. Fonte: Wikimedia Commons.

Young observou um padrão distinto de luz alternativa e linhas escuras. Quando fontes de luz interferem destrutivamente, as linhas são escuras, mas se elas fazem construtivamente, as linhas são claras.

Outro exemplo de interferência interessante são bolhas de sabão. Estes são filmes muito finos, nos quais a interferência ocorre porque a luz é refletida e refratada nas superfícies que limitam o filme de sabão, acima e abaixo.

Figura 5. Em um filme de sabão fino, um padrão de interferência é formado. Fonte: Pxfuel.

Como o filme é grosso. O resultado é um padrão de cores se a luz incidente for branca.

É porque a luz branca não é monocromática, mas contém todos os comprimentos de onda (frequências) do espectro visível. E cada comprimento de onda parece uma cor diferente.

Pode servir a você: corpos luminosos: características e como elas geram sua própria luz

Exercício resolvido

Dois alto -falantes idênticos operados pelo mesmo oscilador são separados a 3 metros e um ouvinte fica a 6 metros do ponto médio da separação entre os falantes, no ponto ou.

Em seguida, mova -se para o ponto P, a uma distância perpendicular de 0.350 do ponto ou, como mostrado na figura. Lá pare de ouvir o som pela primeira vez. Qual é o comprimento de onda em que o oscilador emite?

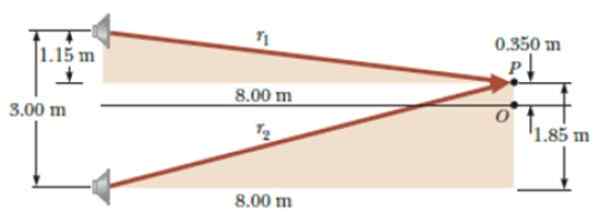Figura 6. Diagrama para o exercício resolvido. Fonte: Serway, r. Física para Ciência e Engenharia.

Solução

A amplitude da onda resultante é 0, portanto a interferência é destrutiva. Se tem que:

Diferença de fase = 2π x│r₁ - r₂│/ λ

Pelo teorema de Pitágoras aplicado aos triângulos sombreados da figura:

r₁ = √1.quinze² + 8² M = 8.08 m; r₂ = √1.85² + 8² M = 8.21 m

│r₁ - r₂│ = │8.08- 8.21 │ M = 0.13 m

Os mínimos ocorrem em λ/2, 3λ/2, 5λ/2 ... o primeiro corresponde a λ/2, então, da fórmula para a diferença de fase é:

λ = 2π x│r₁ - r₂│/ diferença de fase

Mas a diferença de fase entre as ondas deve ser π, de modo que a amplitude para_R = 2a cos (φ/2) ser nulo, então:

λ = 2π x│r₁ - r₂│/ π = 2 x 0.13 m = 0.26 m

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 7. Ondas e física quântica. Editado por Douglas Figueroa (USB).
2. Fisicalab. Interferência de ondas. Recuperado de: fisicalab.com.
3. Giambattista, a. 2010. Física. 2º. Ed. McGraw Hill.
4. Serway, r. Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
5. Wikipedia. Interferência na folha de sono. Fonte: é.Wikipedia.org.