Equilíbrio de matéria o que é, equação geral, tipos

Ele balanço do material É a contagem dos componentes que pertencem a um sistema ou processo em estudo. Esse equilíbrio pode ser aplicado quase a qualquer tipo de sistema, uma vez que se supõe que a soma das massas de tais elementos deve permanecer constante a diferentes medições de medições.

Você pode entender por componente em bolinhas de gude, bactérias, animais, madeira, ingredientes para um bolo; e no caso de química, moléculas ou íons, ou mais especificamente, compostos ou substâncias. Então, a massa total das moléculas que entram em um sistema, com ou sem reação química, deve permanecer constante; contanto que não haja perdas de vazamento.

Na prática, são apresentados inúmeros problemas que podem afetar o equilíbrio da matéria, além de levar em consideração vários fenômenos da matéria e o efeito de muitas variáveis ​​(temperatura, pressão, fluxo, agitação, tamanho do reator, etc.).

No papel, no entanto, os cálculos do equilíbrio da matéria devem coincidir; isto é, a massa de compostos químicos não deve desaparecer a qualquer momento. Fazer esse equilíbrio é análogo para colocar uma pilha de rochas em equilíbrio. Se uma das massas ficar fora do lugar, tudo está desmoronando; Nesse caso, isso significaria que os cálculos estão errados.

Equação de balanço de sujeito geral

Em todos os sistemas ou processo, deve primeiro ser definido como são suas fronteiras. A partir deles, será sabido o que os compostos entram ou saem. É conveniente fazê -lo, especialmente se houver várias unidades de processo a serem consideradas. Quando todas as unidades ou subsistemas são considerados, se fala de um balanço patrimonial de matéria geral.

Esse equilíbrio tem uma equação, que pode ser aplicada a qualquer sistema que obedece à lei da conservação em massa. A equação é a seguinte:

Pode atendê -lo: choreto de chumbo: propriedades, estrutura, usos

E + G - S - C = A

Onde e é a quantidade de matéria que entra Para o sistema; G é o que eu sei gerar Se uma reação química ocorre no processo (como em um reator); S é o que sai do sistema; C é o que eu sei consumir, Novamente, se houver uma reação; E finalmente, é o que eu sei acumula.

Simplificação

Se no sistema ou processo estudado, não há reação química, G e C valem zero. Assim, a equação permanece:

E - s = a

Se o sistema também for considerado no estado estacionário, sem mudanças apreciáveis ​​nas variáveis ​​ou fluxos dos componentes, diz -se que nada se acumula dentro. Portanto, vale a pena zero, e a equação acaba simplificando ainda mais:

E = s

Isto é, a quantidade de matéria que entra é igual à que sai. Nada pode ser perdido ou desaparecer.

Por outro lado, se houver uma reação química, mas o sistema estiver no estado estacionário, G e C terão valores e continuarão sendo zero:

E + G - S - C = 0

E + g = s + c

O que significa que em um reator a massa dos reagentes que entram e dos produtos que geram nele é igual à massa dos produtos e reagentes que saem, e dos reagentes consumidos.

Exemplo de seu uso: peixe no rio

Suponha que o número de peixes em um rio esteja sendo estudado, cujas margens vêm para representar a fronteira do sistema. Sabe -se que, em média, 568 peixes entram por ano, 424 nascem (gerar), 353 morre (consumo) e 236 emigrar ou sair.

Aplicando a equação geral então você tem:

568 + 424 - 353 - 236 = 403

Isso significa que, por 403 peixes, eles se acumulam no rio; isto é, por ano o rio enriquece mais peixes. Se eu tivesse um valor negativo, significaria que o número de peixes está diminuindo, talvez para impactos ambientais negativos.

Pode servir a você: Força Iônica: Unidades, como calculá -lo, exemplos

Pessoal

A partir da equação geral, você pode pensar que existem quatro equações para diferentes tipos de processos químicos. No entanto, o equilíbrio da matéria é dividido em dois tipos de acordo com outro critério: tempo.

Equilíbrio diferencial

No equilíbrio de matéria diferencial, há a quantidade de componentes dentro de um sistema em um determinado tempo ou tempo. Essas quantidades de massa são expressas com unidades de tempo e, portanto, representam velocidades; Por exemplo, kg/h, indicando quantos quilômetros entram, saem, acumulam, geram ou consumem em uma hora.

Para que haja massa (ou fluxos volumétricos, com a densidade à mão), o sistema geralmente deve estar aberto.

Equilíbrio integral

Quando o sistema é fechado, como as reações realizadas em reatores intermitentes (tipo de lote), as massas de seus componentes geralmente interessam antes e depois do processo; isto é, entre os tempos iniciais e finais.

Portanto, as quantidades são expressas como meras massas e não velocidades. Esse tipo de equilíbrio é feito mentalmente quando um liquidificador é usado: a massa dos ingredientes que entram deve ser igual à que deixa após o motor.

Exemplo de exercício

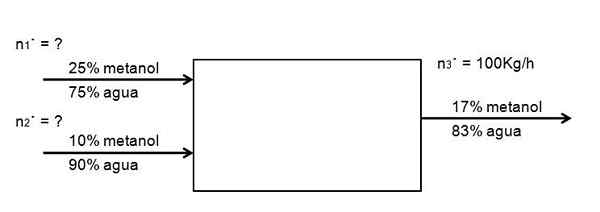
É desejado diluir um fluxo de uma solução de metanol a 25% na água, com outra concentração de 10%, mais diluída, de tal maneira que 100 kg/h são gerados a partir de uma solução de metanol a 17%. Quanto de ambas as soluções de metanol, em 25 e 10%, devem entrar no sistema por hora para conseguir isso? Suponha que o sistema esteja em estado estacionário

Pode atendê -lo: Saponificação

O diagrama a seguir exemplifica a declaração:

Diagrama de fluxo para a diluição da diluição da solução de metanol. Fonte: Gabriel Bolívar.

Não há reação química, então a quantidade de metanol que entra deve ser igual à que sai:

E_Metanol = S_Metanol

0,25 n₁^· + 0,10 n₂^· = 0,17 n₃^·

Apenas o valor de n é conhecido₃^·. O resto é desconhecido. Para resolver esta equação de duas incógnitas, é necessário outro equilíbrio: o da água. Em seguida, fazer o mesmo equilíbrio para a água é:

0,75 n₁^· + 0,90 n₂^· = 0,83 n₃^·

O valor de n é limpo para a água₁^· (Também pode ser n₂^·):

n₁^· = (83 kg/h - 0,90n₂^·)/ (0,75)

Substituindo então n₁^· Na equação do equilíbrio de matéria para metanol e resolução de n₂^· se tem:

0,25 [(83 kg/h - 0,90n₂^·)/ (0,75)] + 0,10 n₂^· = 0,17 (100 kg/h)

n₂^· = 53,33 kg/h

E para obter n₁^· Apenas subtraia:

n₁^· = (100-53,33) kg/h

= 46,67 kg/h

Portanto, por hora, você deve entrar no sistema de 46,67 kg de solução de 25%de metanol e 53,33 kg da solução a 10%.

Referências

1. Felder e Rousseau. (2000). Princípios elementares de processos químicos. (Segunda edição.). Addison Wesley.
2. Fernández Germán. (20 de outubro de 2012). Definição de equilíbrio da matéria. Recuperado de: indústria.líquido