Volume atômico

O que é volume atômico?

Ele Volume atômico É um valor relativo que indica a relação entre a massa molar de um elemento e sua densidade. Então, este volume depende da densidade do elemento, e a densidade depende da fase e de como os átomos são ordenados neste.

De modo que o volume atômico para um elemento z não é o mesmo em outra fase diferente daquela que exibe à temperatura ambiente (líquido, sólido ou gás) ou quando faz parte de certos compostos. Assim, o volume atômico de Z no composto ZB é diferente do z no composto ZB.

Porque? Para entender, é necessário comparar os átomos com, por exemplo, algumas bolinhas de gude. Os bolinhas têm sua borda material muito bem definida, o que é observado graças à sua superfície brilhante. Por outro lado, a borda dos átomos é difusa, embora possam ser considerados remotamente esféricos.

Assim, o que determina um ponto além da borda atômica é a probabilidade de vazio de encontrar um elétron, e esse ponto pode estar mais ou mais próximo do núcleo, dependendo de quantos átomos vizinhos interagem ao redor do átomo em consideração.

Volume atômico e rádio

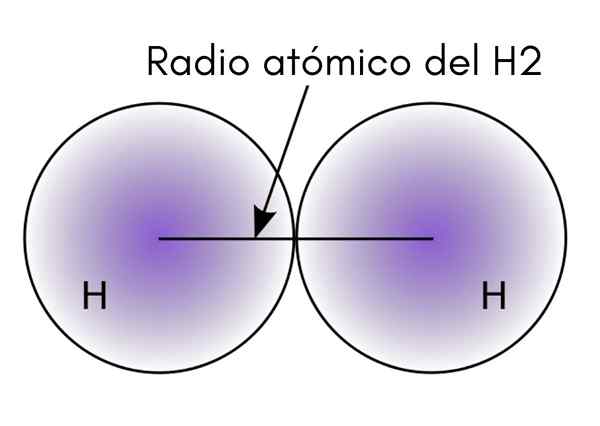
Ao interagir dois átomos H na molécula H₂, As posições de seus núcleos são definidas, bem como as distâncias entre eles (distâncias internucleares). Se ambos os átomos são esféricos, o raio é a distância entre o núcleo e a borda difusa:

Na imagem superior, pode -se ver como a probabilidade de encontrar um elétron diminui à medida que se afasta do núcleo. Dividindo por dois a distância internuclear, o raio atômico é obtido. Então, assumindo uma geometria esférica para átomos, a fórmula é usada para calcular o volume de uma esfera:

V = (4/3) (pi) r³

Nesta expressão r é o raio atômico determinado para a molécula H₂. O valor V calculado por esse pequeno método preciso pode mudar se, por exemplo, h for considerado₂ em estado líquido ou metálico. No entanto, esse método é muito impreciso porque as formas de átomos estão muito longe da esfera ideal em suas interações.

Para determinar os volumes atômicos em sólidos, muitas variáveis ​​relativas ao arranjo são levadas em consideração e que são obtidas por estudos de difração de raio X.

Fórmula adicional

A massa molar expressa a quantidade de matéria que tem uma toupeira de átomos de um elemento químico.

Suas unidades são g/mol. Por outro lado, a densidade é o volume que ocupa um grama do elemento: g/ml. Como as unidades de volume atômico são ML/mol, você precisa brincar com as variáveis ​​para atingir as unidades desejadas:

• (g/mol) (ml/g) = ml/mol/mol

Ou o que é o mesmo:

• (Massa molar) (1/d) = V
• (Massa molar/d) = V

Assim, o volume de uma mole de átomos de um elemento pode calcular facilmente; enquanto com a fórmula do volume esférico, o volume de um átomo individual é calculado.

Para atingir esse valor a partir do primeiro, é necessária uma conversão através do número Avogadro (6,02,10^-23).

Como varia o volume atômico na tabela periódica?

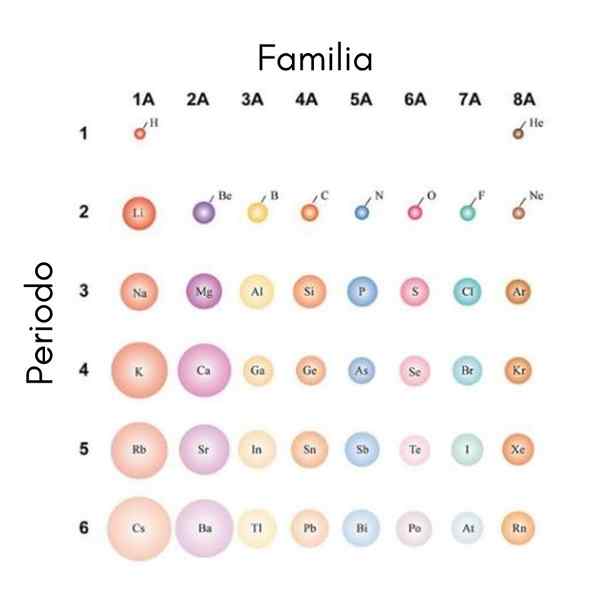
Se os átomos forem considerados esféricos, sua variação será a mesma observada em rádios atômicos. Na imagem superior, que mostra os elementos representativos, é ilustrado que da direita para a esquerda dos átomos anões; Por outro lado, de cima para baixo, eles ficam mais volumosos.

Isso ocorre porque no mesmo período o núcleo incorpora prótons à medida que se move para a direita. Esses prótons exercem uma força de atração em elétrons externos, que parecem uma carga nuclear eficaz z_Ef, menor que a carga nuclear real z.

Os elétrons das camadas internas repelem as da camada externa, reduzindo o efeito do núcleo nelas; Isso é conhecido como efeito de tela. No mesmo período, o efeito da tela falha em neutralizar o aumento do número de prótons, de modo que os elétrons da camada interna não impedem a contração dos átomos.

No entanto, ao descer em um grupo, novos níveis de energia são ativados, o que permite que os elétrons orbitem o núcleo. Da mesma forma, o número de elétrons na camada interna é aumentado, cujos efeitos de blindagem começam a ser diminuídos se o núcleo adicionar prótons novamente.

Por esses motivos, é apreciado que o Grupo 1A tenha os átomos mais volumosos, ao contrário dos pequenos átomos do grupo 8a (ou 18), o de gases nobres.

Volumes atômicos de metais de transição

Os átomos dos metais de transição incorporam elétrons em orbitais internos D. Esse aumento no efeito da tela e, assim como a carga nuclear real, é quase igualmente anulada, de modo que seus átomos mantêm tamanho semelhante no mesmo período.

Em outras palavras: em um período, os metais de transição exibem volumes atômicos semelhantes. No entanto, essas pequenas diferenças são enormemente significativas ao definir cristais de metal (como se fossem mármores metálicos).

Exemplos de volume atômico

Duas fórmulas matemáticas estão disponíveis para calcular o volume atômico de um elemento, cada uma com seus exemplos correspondentes.

Exemplo 1

Dado o radioglogênio atômico -37 pm (1 picômetro = 10^-12m)-e o césio -265 pm-, calcule seus volumes atômicos.

Usando a fórmula de volume esférico, você tem: então:

V_H= (4/3) (3.14) (37 pm)³= 212,07 pm³

V_Cs= (4/3) (3.14) (265 pm)³= 77912297.67 pm³

No entanto, esses volumes expressos nos picômetros são exorbitantes; portanto, eles se transformam em unidades de Angstroms, multiplicando -as pelo fator de conversão (1å/100pm)³:

(212,07³) (1å/100pm)³= 2.1207 × 10^-4 PARA³

(77912297.67³) (1å/100pm)³= 77.912 ų

Assim, as diferenças de tamanho entre o átomo H pequeno e o átomo volumoso de Cs são numericamente evidenciadas. É necessário levar em consideração que esses cálculos nada mais são do que aproximações sob a afirmação de que um átomo é totalmente esférico, o que divaga a realidade.

Exemplo 2

A densidade do ouro puro é 19,32 g/ml e sua massa molar é 196,97 g/mol. Aplicando a fórmula M/D para calcular o volume de uma toupeira de átomos de ouro, o seguinte é:

V_Au= (196,97 g/mol)/(19,32 g/ml) = 10,19 ml/mol/mol

Isto é, que 1 mol de átomos de ouro ocupa 10,19 ml, mas que volume ocupa um átomo de ouro especificamente? E como expressá -lo em unidades de PM³? Para isso, basta aplicar os seguintes fatores de conversão:

(10,19 ml/mol) · (mol/6,02 · 10^-23 átomos) · (1 m/100 cm)³· (13:00/10^-12m)³= 16,92 · 10⁶ PM³

Por outro lado, o raio atômico do ouro é 166. Se ambos os volumes forem comparados - o obtido pelo método anterior e que é calculado com a fórmula do volume esférico -, será encontrado que eles não têm o mesmo valor:

V_Au= (4/3) (3.14) (166 pm)³= 19,15 · 10⁶ PM³

Qual dos dois está mais próximo do valor aceito? Aquele que está mais próximo dos resultados experimentais obtidos pela difração de raio x da estrutura cristalina do ouro.