Velocidade aréolar como é calculado e resolvido exercícios

O Velocidade areolar É a área de varredura por unidade de tempo e é constante. É típico de cada planeta e surge da descrição da segunda lei de Kepler de maneira matemática. Neste artigo, explicaremos o que ele consiste e como é calculado.

O boom que representa a descoberta de planetas fora do sistema solar reativou o interesse no movimento planetário. Nada acredita que esses planetos de exo seguem leis diferentes daquelas já conhecidas e válidas do sistema solar: as leis de Kepler.

Johannes Kepler foi o astrônomo que, sem a ajuda do telescópio e usando as observações de seu mentor Tycho Brahe, criou um modelo matemático que descreve o movimento dos planetas ao redor do sol.

Ele deixou esse modelo expresso nas três leis que suportam seu nome e que permanecem tão válidas hoje como em 1609, quando estabeleceu os dois e 1618 primeiros, data em que o terceiro.

[TOC]

Leis de Kepler

No idioma atual, as três leis de Kepler dizem assim:

1. As órbitas de todos os planetas são elípticas e o sol está em um foco.

2. O vetor de posição que vai do sol para um planeta varre áreas iguais em tempos iguais.

3. O quadrado do período orbital de um planeta é proporcional ao cubo da semi-weise da elipse descrita.

Um planeta terá uma velocidade linear, como qualquer objeto conhecido que se mova. E há mais: ao escrever a segunda lei de Kepler em forma matemática, surge um novo conceito chamado Areolar Speed, típico de cada planeta.

Por que os planetas se movem elipticamente ao redor do sol?

A Terra e os outros planetas se movem ao redor do sol, graças ao fato de que exerce uma força sobre eles: a atração gravitacional. O mesmo vale para qualquer outra estrela e os planetas que estão em conformidade com o seu sistema, se você os tiver.

Pode servir a você: calor sensível: conceito, fórmulas e exercícios resolvidos

Esta é uma força do tipo conhecido como força central. O peso é uma força central com a qual todos estão familiarizados. O objeto que exerce a força central, seja o sol ou uma estrela distante, atrai os planetas em direção ao centro e eles se movem descrevendo uma curva fechada.

Em princípio, essa curva pode ser aproximada como uma circunferência, como Nicolás Copernico, um criador de astrônomo polonês da teoria heliocêntrica, fez.

Força responsável é a atração gravitacional. Essa força depende diretamente das massas da estrela e do planeta em questão e é inversamente proporcional ao quadrado da distância que as separa.

O problema não é tão fácil, porque em um sistema solar, todos os elementos interagem dessa maneira, adicionando complexidade ao assunto. Eles também não são partículas, pois estrelas e planetas são de tamanho mensurável.

Por esse motivo, o ponto central da órbita ou circuito percorrido pelos planetas não está exatamente centrado na estrela, mas em um ponto conhecido como o centro de gravidade do sistema Sol-Planet.

A órbita resultante é elíptica. A imagem a seguir mostra, tomando como exemplo a terra e o sol:

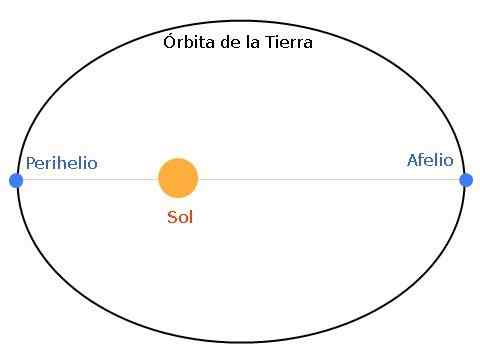figura 1. A órbita da terra é elíptica, com o sol localizado em um dos focos. Quando a terra e o sol estão à sua distância máxima, diz -se que a terra está em afélio. E se a distância for mínima, falamos sobre periélio.

O apelium é a posição mais distante da terra ao sol, enquanto o periélio é o ponto mais próximo. A elipse pode ser mais ou menos achatada, de acordo com as características do sistema estelar - planeta.

Os valores de ASELS e Perihélio variam anualmente, já que os outros planetas causam distúrbios. Para outros planetas, essas posições são chamadas de suporte e experiência, respectivamente.

A magnitude da velocidade linear de um planeta não é constante

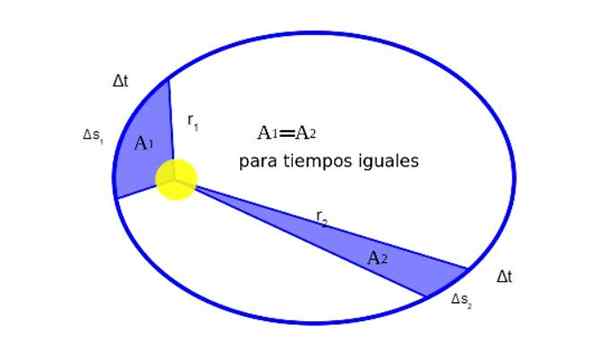
Kepler descobriu que, quando um planeta orbita ao redor do sol, durante o movimento Barr Motion Igual áreas em tempos iguais. A Figura 2 mostra graficamente o significado disso:

Pode atendê -lo: qual é o equilíbrio da partícula? (Com exemplos)Figura 2. O vetor de posição de um planeta em relação ao sol é r. Quando o planeta descreve sua órbita viaja um arco de elipse em um tempo Δt.

Matematicamente, o fato de que₁ ser igual a₂ É expresso assim:

As rotas de arcos são pequenas, para que cada área possa se aproximar da de um triângulo:

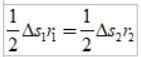
AS ΔS =vΔt, Onde v é a velocidade linear do planeta em um determinado ponto, ao substituir que temos:

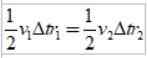
E como o intervalo de tempo Δt é o mesmo, é obtido:

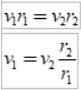
Como r₂ > r₁, então v₁ > v₂, Em outras palavras, a velocidade linear de um planeta não é constante. De fato, a terra está indo mais rápido quando está no periélio do que quando está no afélio.

Portanto, a velocidade linear da terra ou qualquer planeta ao redor do sol não é uma magnitude que serve para caracterizar o movimento do referido planeta.

Velocidade areolar

A segunda lei de Kepler sugere uma nova magnitude chamada Areolar Speed. É definido como a área varrida por unidade de tempo e é constante. Para calculá -lo, a figura a seguir é usada:

Figura 3. O vetor de posição da Terra (ou planeta) em relação ao sol é r e, ao se mover, a Terra experimenta um deslocamento, também o vetor Δr.

Uma pequena área varrida pela Terra é escolhida enquanto realiza seu circuito elíptico, que indicaremos como ΔA. O tempo necessário para isso é Δt.

A Figura 3 mostra o vetor de posição da Terra em relação ao sol, indicado por R. Quando a Terra se mover, experimente um deslocamento ΔR.

Esta área corresponde a metade da área do retângulo mostrada na Figura 3:

O quociente Δr/Δt é precisamente a velocidade linear da terra, de modo que a velocidade areolar permanece:

V_PARA No sistema internacional eles são:

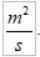
Observe que, embora R e V varie, o produto permanece constante. Isso transforma a velocidade aréolar em uma magnitude muito adequada para caracterizar o movimento de um planeta ao redor de sua estrela.

Pode atendê -lo: Constantes Antoine: fórmulas, equações, exemplos

O produto de R e V é a magnitude do momento angular L, para que a velocidade areolar possa ser expressa como:

Calculando velocidade linear e velocidade areolar

Com o exemplo a seguir, mostraremos como calcular a velocidade areolar quando alguns parâmetros do movimento planetário forem conhecidos:

Exercício

Uma planalta exo se move ao redor de seu sol após uma órbita elíptica, de acordo com as leis de Kepler. Quando está no Expertro, seu vetor de rádio é r₁ = 4 · 10⁷ km, e quando está no suporte é r₂ = 15 · 10⁷ km. A velocidade linear em sua experiência é V₁ = 1000 km/s.

Calcular:

A) A magnitude da velocidade no suporte.

B) a velocidade areolar da planet exo.

C) A duração do eixo principal elipse principal.

Responda para)

A equação é usada:

em que valores numéricos são substituídos.

Cada termo é identificado da seguinte forma:

v₁ = Velocidade no suporte; v₂ = Velocidade no especialista; r₁= Distância do autor,

r₂= Distância do especialista.

Com esses valores, é obtido:

Resposta b)

A equação a ser usada é

em que o par de valores r e v do Expertro ou o suporte pode ser substituído, pois V_PARA É uma constante do planeta:

Resposta c)

A duração do grande eixo da elipse é o semi -semi -semi -semi -semi -seismum e a experiência:

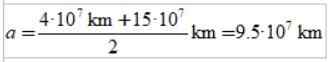
Bibliografia

1. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. México. Editores de aprendizado do Cengage. 367-372.
2. Stern, d. (2005). As três leis de Kepler do movimento planetário. Recuperado do PWG.GSFC.Panela.Gov
3. Nota: O exercício proposto foi realizado e modificado a partir do texto a seguir de um livro de McGrawhill. Infelizmente, é um capítulo isolado em formato PDF, sem o título ou o autor: mheducation.Es/bcv/guia/capítulo/844817027x.Pdf