Propriedades, exemplos, exercícios de vetores gratuitos

O vetores gratuitos Eles são aqueles que são totalmente especificados por sua magnitude, sua direção e seu significado, sem ser necessário indicar um ponto de aplicação ou uma origem específica.

Como vetores infinitos podem ser desenhados dessa maneira, um vetor livre não é uma entidade única, mas um conjunto de vetores paralelos e idênticos que são independentes do local onde estão localizados.

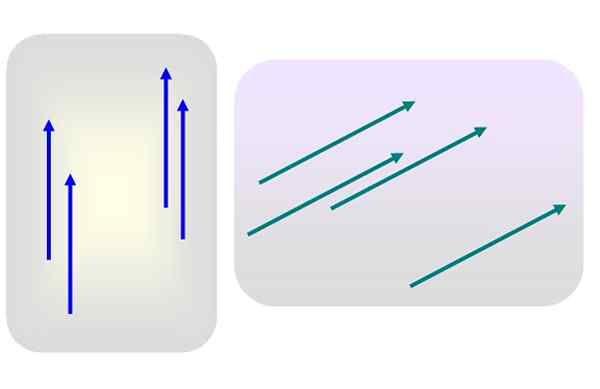
figura 1. Vários vetores livres. Fonte: Self feito.

Digamos que existem vários vetores de magnitude 3 direcionados verticalmente para cima, ou magnitude 5 e inclinados para a direita, como na Figura 1.

Nenhum desses vetores é aplicado especificamente a algum ponto. Então, qualquer um dos vetores azuis ou verdes é representativo de seu respectivo grupo, uma vez que suas características - módulo, direção e sentido - não são modificadas quando são transferidas para outro lugar do plano.

Um vetor livre é geralmente indicado no texto impresso com uma letra minúscula e ousada, por exemplo v. Ou com minúsculas e uma flecha no topo, se for um texto de manuscrito.

[TOC]

 Exemplos

A vantagem que os vetores livres têm é que eles podem ser movidos por plano ou espaço e manter suas propriedades, uma vez que qualquer representante do conjunto é igualmente válido.

É por isso que na física e mecânica são frequentemente usados. Por exemplo, para indicar a velocidade linear de um sólido que se move, não é necessário escolher um ponto específico do objeto. Então o vetor de velocidade se comporta como um vetor livre.

Outro exemplo de vetor livre é o par de forças. A par Consiste em duas forças de igual magnitude e direção, mas de sentidos opostos, aplicados em diferentes pontos de um sólido. O efeito de um par não é transferir o objeto, mas causar uma rotação graças ao momento produzido.

A Figura 2 mostra um par de forças aplicadas a um volante. Através das forças F₁ e F₂, O torque que gira o volante em torno do centro é criado e em um cronograma.

Pode servir a você: nitreto de boro (BN): estrutura, propriedades, obtenção, uso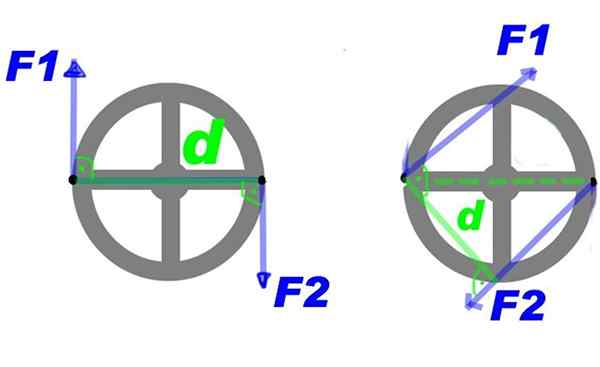 Figura 2. Algumas forças aplicadas a um volante fornece uma curva de pontuação. Fonte: Bensko [domínio público].

Você pode fazer algumas alterações no par e continuar a obter o mesmo efeito rotativo, por exemplo, aumentar a força, mas diminuir a distância entre eles. Ou manter força e distância, mas aplique o par em mais alguns pontos no volante, ou seja, gire o torque ao redor do centro.

O tempo do par de forças ou simplesmente par, É um vetor cujo módulo é Fd e é perpendicular ao plano da roda perpendicular. No exemplo mostrado pela convenção, o tempo de tempo faz sentido negativo.

Propriedades e características

Ao contrário do vetor livre V, os vetores Ab e CD Eles são fixos (veja a Figura 3), pois eles especificaram o ponto de partida e o ponto de chegada. Mas sendo equipamentos um com o outro e, por sua vez, com o vetor v, Eles são representativos do vetor livre v.

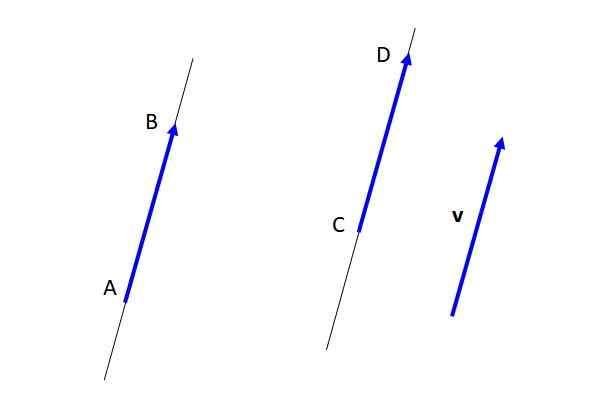Figura 3. Vetores gratuitos, equipamentos e vetores fixos. Fonte: Self feito.

As principais propriedades dos vetores livres são os seguintes:

-Qualquer vetor Ab (Veja a Figura 2) É, como afirmado, representativo do vetor livre v.

-O módulo, direção e significado são os mesmos em qualquer representante de vetor livre. Na Figura 2, os vetores Ab e CD Eles representam o vetor livre v E eles são equipamentos.

-Dado um ponto P do espaço, é sempre possível encontrar um representante de vetor livre v cuja origem está em P e disse que o representante é único. Esta é a propriedade mais importante dos vetores livres e a que os torna tão versáteis.

Pode atendê -lo: Europa (satélite): características, composição, órbita, movimento

-Um vetor livre viajado é denotado como 0 E é o conjunto de todos os vetores que não têm magnitude, direção e significado.

-Se o vetor Ab representa o vetor livre v, Então o vetor BA representa o vetor livre -v.

-Notação será usada V³ para designar o conjunto de todos os vetores sem espaço e V² Para designar todos os vetores livres do avião.

Exercícios resolvidos

Com vetores gratuitos, você pode executar as seguintes operações:

-Adição

-Subtração

-Multiplicação de escalada por um vetor

-Produto escalar entre dois vetores.

-PRODUTO CRIME

-Combinação linear de vetores

E mais.

-Exercício 1

Um aluno pretende nadar de um ponto na costa de um rio para outro que é precisamente na frente. Para não conseguir nada diretamente a uma velocidade de 6 km / h, em direção perpendicular, no entanto, a corrente tem uma velocidade de 4 km / h que a desvia.

Calcule a velocidade resultante do nadador e quanto é desviado pela corrente.

Solução

A velocidade prolongada do nadador é a soma vetorial de sua velocidade (em relação ao rio, desenhada verticalmente para cima) e a velocidade do rio (desenhada da esquerda para a direita), que é realizada conforme indicado na figura abaixo:

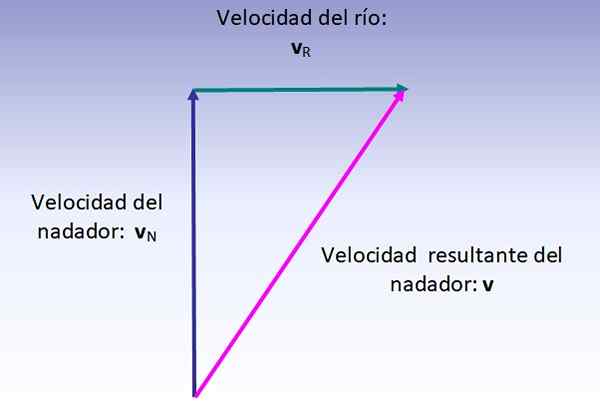
A magnitude da velocidade resultante corresponde à hipotenusa do triângulo certo mostrado, portanto:

V = (6² + 4²) ^½ km/h = 7.2 km/h

O endereço pode ser calculado pelo ângulo em relação à perpendicular à costa:

α = arctg (4/6) = 33.7 ou 56.3º sobre a costa.

Exercício 2

Encontre o tempo do par de forças mostradas na figura:

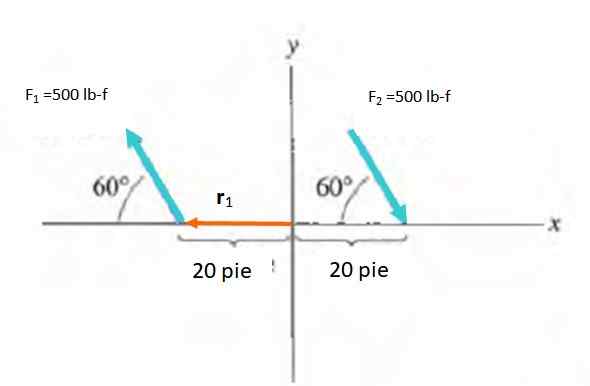
Solução

O momento é calculado por:

Pode atendê -lo: choques inelásticos: em uma dimensão e exemplos

M = r x F

As unidades do momento são LB-F.pé. Como o torque está no plano da tela, o momento é direcionado perpendicularmente a ele, para fora ou para dentro.

Como o torque do exemplo tende a girar o objeto em que é aplicado (que não é mostrado na figura) em um cronograma, esse momento é considerado apontando dentro da tela e com um sinal negativo.

A magnitude do momento é m = f.d.sin a, estar no ângulo entre a força e o vetor r. Você tem que escolher um ponto para calcular o momento, que é um vetor livre. A origem do sistema de referência é escolhida, portanto r vai de O ao ponto de aplicação de cada força.

M₁ = M₂ = -Fdsen60º = -500 . vinte .Sen 60º lb-f . pé = -8660.3 lb-f . pé

O momento líquido é a soma de M₁ e m₂: -17329.5 lb-f . pé.

Referências

1. Beardon, t. 2011. Uma introdução aos vetores. Recuperado de: nrich.Matemáticas.org.
2. Bedford, 2000. PARA. Mecânica para engenharia: estático. Addison Wesley. 38-52.
3. Figueroa, d. Série: Física para Ciência e Engenharia. Volume 1. Cinemática.31-68.
4. Físico. Módulo 8: vetores. Recuperado de: FRTL.Utn.Edu.ar
5. Hibbeler, R. 2006. Mecânica para engenheiros. Estático. 6ª edição. Empresa editorial continental. 15-53.
6. Vetor da calculadora de adição. Recuperado de: 1728.org
7. Vetores. Recuperado de: é.Wikibooks.org