Cálculo vetorial resultante, exemplos, exercícios

Ele vetor resultante É o obtido por uma operação com vetores cujo resultado também é um vetor. Normalmente, esta operação é a soma de dois ou mais vetores, através dos quais um vetor é obtido cujo efeito é equivalente.

Dessa maneira, vetores como velocidade, aceleração ou força são obtidos resultantes. Por exemplo, quando várias forças agem em um corpo F₁, F₂, F₃,.. . A soma vetorial de todas essas forças é equivalente à força líquida (o resultante), que se expressa matematicamente:

F₁ + F₂ + F₃ +… = F_R  qualquer F_N

figura 1. O peso da neve é ​​distribuído sobre o teto e sua ação pode ser substituída por uma única força resultante aplicada no local apropriado. Fonte: Pixabay.

O vetor resultante, seja forças ou qualquer outra magnitude do vetor, está aplicando as regras da soma dos vetores. Como os vetores têm direção e sentido, além do valor numérico, não é suficiente adicionar os módulos para ter o vetor resultante.

Isso é verdade apenas no caso em que os vetores envolvidos estão na mesma direção (ver exemplos). Caso contrário, é necessário usar métodos de soma vetorial, que, dependendo do caso, podem ser geométricos ou analíticos.

[TOC]

Exemplos

Os métodos geométricos para encontrar o vetor resultante são o método polígono e o método do paralelogramo.

Quanto aos métodos analíticos é o método do componente, através do qual o vetor resultante de qualquer sistema vetorial pode ser encontrado, desde que tenhamos seus componentes cartesianos.

Métodos geométricos para adicionar dois vetores

Suponha que os vetores ou e v (Nós os denotamos em negrito para distingui -los do escalar). Na Figura 2) temos eles localizados no avião. Na Figura 2 b) se moveu para o vetor V de tal maneira que sua origem coincide com o fim de ou. O vetor resultante vai da origem do primeiro (ou) até a ponta do último (v):

Pode servir a você: compressibilidade: sólidos, líquidos, gases, exemplos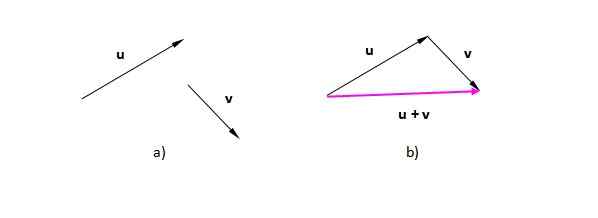 Figura 2. O vetor resultante da soma gráfica dos vetores. Fonte: Self feito.

A figura que resulta neste caso é um triângulo (um triângulo é um polígono de 3 anos). Se tivermos dois vetores na mesma direção, o procedimento é o mesmo: coloque um dos vetores após o outro e desenhe um que vai da origem ou cauda da primeira até a ponta ou fim do último.

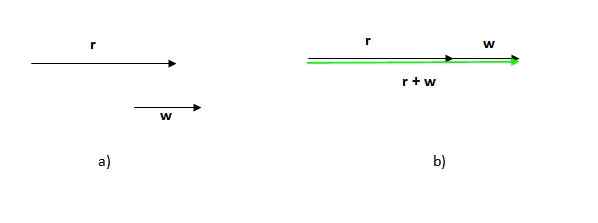
Observe que a ordem em que este procedimento é feito não importa, pois a soma dos vetores é comutativa.

Observe também que neste caso o módulo (O comprimento ou tamanho) do vetor resultante é a soma dos módulos dos vetores adicionais, diferentemente do caso anterior, no qual o módulo vetorial resultante é menor que a soma dos módulos dos participantes.

Método do paralelogramo

Este método é muito apropriado quando você precisa adicionar dois vetores cujos pontos de origem concordam, com a origem de um sistema de coordenadas x-y. Suponha que este seja o caso de nossos vetores ou e v (Figura 3):

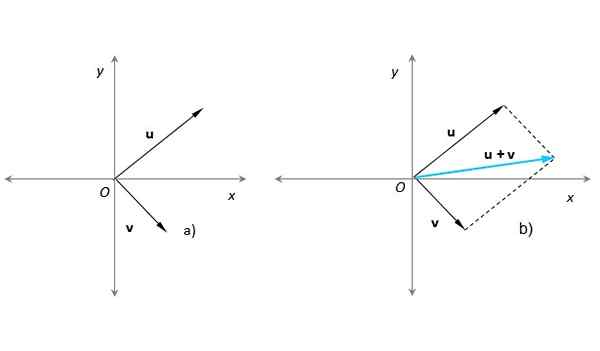Figura 3. Soma de dois vetores por meio do método do paralelogramo com o vetor resultante em azul turquesa. Fonte: Self feito.

Na Figura 3b) um paralelogramo foi construído com a ajuda de linhas pontilhadas paralelas para ou já v. O vetor resultante tem sua origem em O e seu fim no ponto em que as linhas pontilhadas se cruzam. Este procedimento é completamente equivalente ao descrito na seção anterior.

Exercícios

-Exercício 1

Dados os seguintes vetores, encontre o vetor resultante usando o método poligonal.

Pode servir a você: reflexão leve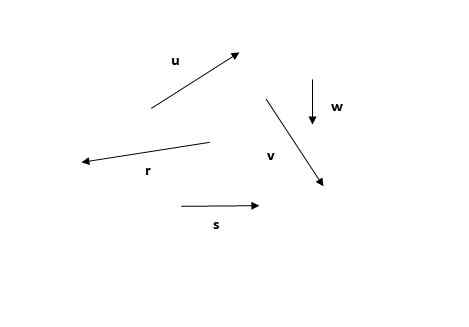 Figura 4. Vetores para encontrar seu resultante através do método poligonal. Exercício 1. Fonte: Self feito.

Solução

O método poligonal é o primeiro dos métodos vistos. Lembre -se de que a soma dos vetores é comutativa (a ordem das adições não altera a soma), para que você possa começar com qualquer um dos vetores, por exemplo ou (Figura 5a) ou r (Figura 5b):

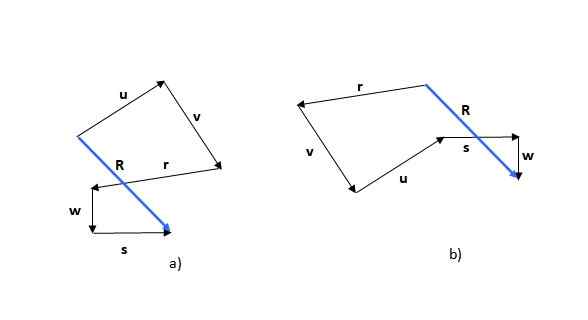Figura 5. Soma dos vetores através do método poligonal. Fonte: Self feito.

A figura obtida é um polígono e o vetor resultante (em azul) é chamado R. Se você começar com outro vetor, a figura formada pode ser diferente, como pode ser visto no exemplo, mas o vetor resultante é o mesmo.

Exercício 2

Na figura seguinte, sabe -se que os módulos dos vetores ou e v respectivamente são u = 3 unidades arbitrárias e v = 1.8 unidades arbitrárias. O ângulo que ou a forma com o eixo x positivo é de 45 º, enquanto v Formulário 60 º com o eixo y, como visto na figura. Encontre o vetor, magnitude e direção resultante.

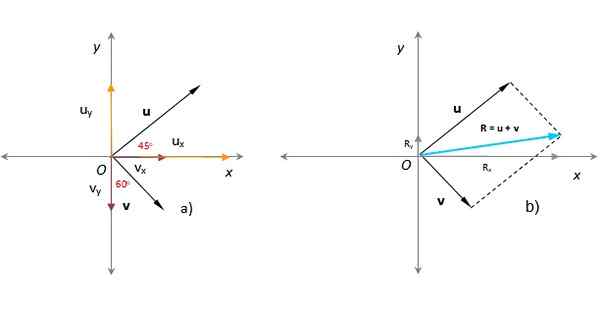
Solução

Na seção anterior, o vetor resultante foi encontrado aplicando o método do paralelogramo (em turquesa na figura).

Uma maneira simples de encontrar o vetor resultante analiticamente é expressar os vetores adicionando em termos de seus componentes cartesianos, o que é uma tarefa fácil quando o módulo e o ângulo são conhecidos, como os vetores deste exemplo:

ou_x = u . cos 45º = 3 x cos 45 º = 2.12; ou_e = u . sin 45 º = 3x sen 45º = 2.12

v_x = v . Sen 60º = 1.8 x sen 60 º = 1.56; v_e = -V . cos 60 º = -1.8 x cos 60º = - 0.9

Pode atendê -lo: movimento pendular

Os vetores ou e v São vetores pertencentes ao avião, tendo dois componentes cada. O vetor U está no primeiro quadrante e seus componentes são positivos, enquanto o Vector V está no quarto quadrante; Seu componente X é positivo, mas sua projeção no eixo vertical cai no eixo e negativo.

Cálculo dos componentes cartesianos do vetor resultante

O vetor resultante está adicionando algebraicamente os respectivos componentes x e y, para obter seus componentes cartesianos:

R_x = 2.12 + 1.56 = 3.68

R_e = 2.12 + (-0.9) = 1.22

Uma vez que os componentes cartesianos foram especificados e o vetor é conhecido completamente. O vetor resultante pode ser expresso com a notação entre colchetes (Suportes):

R = unidades arbitrárias

A notação do suporte é usada para distinguir um vetor de um ponto no plano (ou no espaço). Outra maneira de expressar o vetor resultante de maneira analítica é através do uso de vetores de unidade Yo e j no avião (Yo, J e k No espaço):

R = 3.68 Yo + 1.22 J unidades arbitrárias

Como ambos os componentes do vetor resultante são positivos, o vetor R Pertence ao primeiro quadrante, que já havia sido visto graficamente.

Magnitude e direção do vetor resultante

Conhecido pelos componentes cartesianos, a magnitude de R é calculada através do teorema de Pitágoras, uma vez que o vetor resultante resultante R, ao lado de seus componentes r_x e r_e Eles formam um triângulo certo:

Magnitude ou módulo: r = (3.68² + 1.22²)^½ = 3.88

Endereço q Tomando o eixo x positivo como referência: q = arcan (r_e / R_x) = arctg (1.22/3.68) = 18.3º

Referências

1. Adicionando vetores e regras. Recuperado de: newt.Phys.UNSW.Edu.Au
2. Figueroa, d. Série: Física para Ciência e Engenharia. Volume 1. Cinemática.31-68.
3. Físico. Módulo 8: vetores. Recuperado de: FRTL.Utn.Edu.ar
4. Hibbeler, R. 2006. Mecânica para engenheiros. Estático. 6ª edição. Empresa editorial continental. 15-53.
5. Vetor da calculadora de adição. Recuperado de: www.1728.org