Cálculo de vetores de balanceador, exemplos, exercícios

Ele Vector de equilíbrio É o que contrasta o vetor resultante e, portanto, é capaz de equilibrar um sistema, pois tem a mesma magnitude e a mesma direção, mas ao contrário disso.

Em várias ocasiões, o vetor de equilíbrio refere -se a um vetor de força. Para calcular a força de equilíbrio, a força resultante é a primeira, como mostrado na figura a seguir:

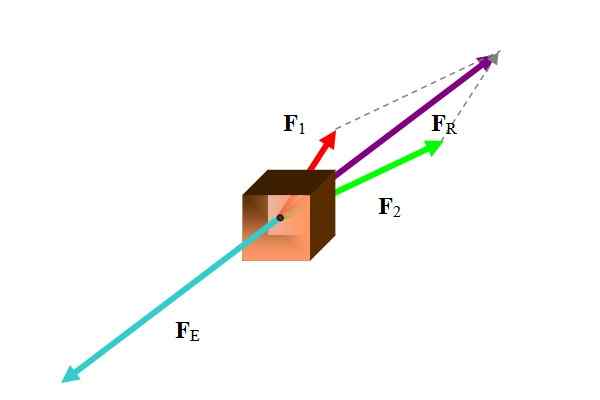
figura 1. Em um corpo, duas forças ato cujo resultante é equilibrado pela força em cor turquesa. Fonte: Self feito.

Existem vários métodos para realizar esta tarefa, de acordo com os dados em questão. Como as forças são vetores, o resultado é a soma vetorial das forças participantes:

F_R = F₁ + F₂ + F₃ +  .. .

Entre os métodos a serem usados ​​estão métodos gráficos, como métodos poligonais, paralelogramados e analíticos, como a decomposição de forças em seus componentes cartesianos. No exemplo, a figura foi usada o método do paralelogramo.

Uma vez que a força resultante é encontrada, a força de equilíbrio é precisamente o vetor oposto.

Sim F_E É a força de equilíbrio, então é cumprida que F_E Aplicado em um determinado momento, garante o equilíbrio da tradução do sistema. Se for uma única partícula, não se moverá (ou talvez o faça com velocidade constante), mas se for um objeto estendido, ainda terá a possibilidade de girar:

F_R + F_E = 0

[TOC]

Exemplos

As forças de equilíbrio estão presentes em todos os lados. Nós mesmos somos equilibrados pela força que a cadeira exerce para compensar o peso. Os objetos encontrados em repouso: livros, móveis, lâmpadas de teto e um grande número de mecanismos, estão sendo continuamente equilibrados por forças.

Pode atendê -lo: choques inelásticos: em uma dimensão e exemplos

Por exemplo, um livro de descanso em uma mesa é equilibrado pela força normal que exerce no livro, impedindo que ele caia. O mesmo vale para a corrente ou cabo que segura a lâmpada que pendura do teto em uma sala. Os cabos que mantêm uma carga são distribuídos de seu peso através da tensão neles.

Em um fluido, alguns objetos são capazes de flutuar e permanecer em repouso, uma vez que seu peso é equilibrado por uma força ascendente exercida pelo líquido, chamado empurrar.

Vários mecanismos precisam ser equilibrados, conhecendo o vetor de força de equilíbrio, como barras, vigas e colunas.

Ao usar um equilíbrio, é necessário equilibrar de alguma forma o peso do objeto com uma força equivalente, adicionando pesos ou por molas.

Tabela de forças

A tabela das forças é usada em laboratório para determinar a força equilibrada. Consiste em uma plataforma circular, da qual você tem a vista superior na figura, e isso tem um transportador para medir os ângulos.

Nas bordas da mesa, existem polias através das quais as cordas mantêm pesos e que convergem em um aro que está no centro.

Por exemplo, dois pesos são pendurados. As tensões geradas nas cordas por esses pesos são desenhadas em vermelho e azul na Figura 2. Um terceiro pesa verde, pode equilibrar a força resultante dos outros dois e manter o sistema em equilíbrio.

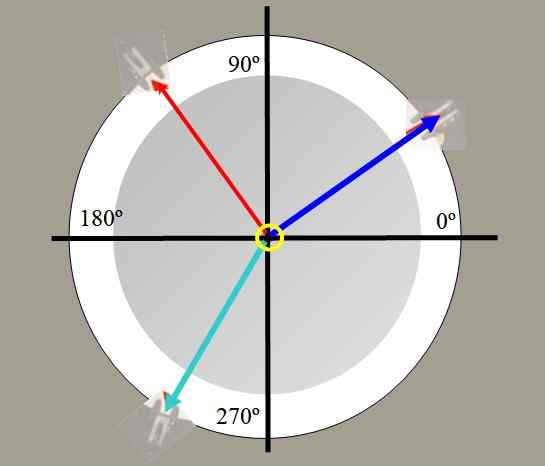Figura 2. Vista do topo da tabela das forças. Fonte: Self feito.

Com a tabela de forças, você pode verificar o caráter vetorial das forças, decompor as forças, encontrar a força de equilíbrio e verificar o teorema de Lamy:

Pode servir você: sol

Sim um O corpo está em equilíbrio graças a três forças coplanares, simultâneas e não colineas (não paralelas), chamadas PARA, B e C, A relação entre essas forças é a seguinte:

A/ sin α = b/ sen β = c/ sen γ

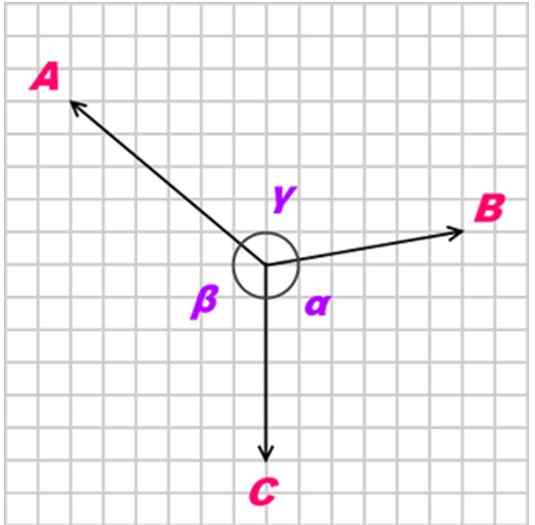Figura 3. O teorema de Lamy se aplica às forças simultâneas e coplanares. Fonte: Wikimedia Commons.

Exercícios resolvidos

-Exercício 1

Na tabela das forças na Figura 2 pesa de 225 g (tensão azul) e 150 g (tensão vermelha) são enforcadas, com os ângulos mostrados. Encontre o valor da força de equilíbrio e o ângulo que essa forma com o eixo vertical.

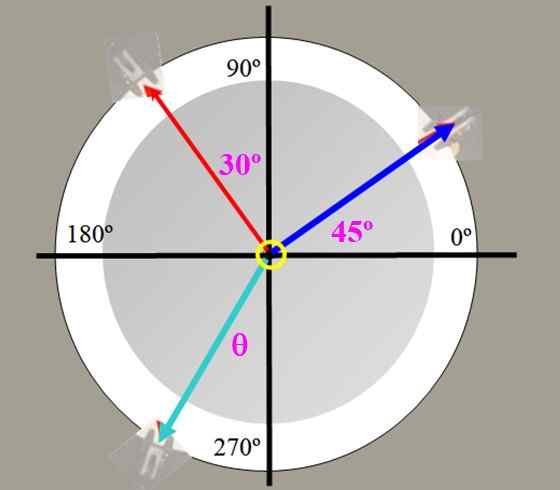Figura 4. Força Tabela para o Exercício 1.

Solução

O problema pode ser trabalhado com os pesos expressos em gramas (forças). Deixe p₁ = 150 gramas e P₂ = 225 gramas, os respectivos componentes de cada um são:

P_1x = 225 . cos 45º g = 159.10 g; P_1y = 225 . cos 45º g = 159.10 g

P_2x = -150 . Sen 30º g = -75.00 g; P_{2 e} = 150 . Cos 30º g = 129.90 g

O peso resultante P_R Os componentes estão adicionando algebricamente:

P_Rx = 159.10 - 75.00 g = 84.10 g

P_Ry = 159.10 + 129.90 g = 289.00 g

O peso de equilíbrio P_E é o vetor oposto P_R:

P_Ex = -84.10 g

P_Ei = -289.00 g

A magnitude do peso de equilíbrio é calculada por:

P_E = (P_Ex² + P_Ei²)^1/2 = ((-84.10)² + (-289.00)²)^1/2 G = 301 g

O ângulo θ da figura é:

θ = arctg (-84.10 / -289.00) = 16.2º em relação ao eixo e negativo.

-Exercício 2

Encontre o vetor de equilíbrio do sistema mostrado na figura, sabendo que cada quadrado mede 10 m de lado.

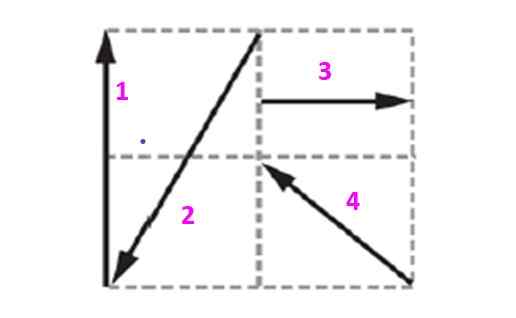Figura 5. Diagrama para o exemplo resolvido 2.

Solução

Os vetores contidos nesta grade serão expressos em termos de unidade e vetores ortogonais Yo e J que determinam o avião. Vetor 1, que será denotado como v₁ Tem magnitude de 20 m e é direcionado verticalmente para cima. Pode ser expresso como:

Pode servir a você: transferência de calor de radiação (com exemplos)

v₁ = 0 Yo +vinte J m

Do desenho, observa -se que o vetor 2 é:

v₂ = -10 Yo - vinte J m

O vetor 3 é horizontal e pontos no endereço positivo:

v₃ = 10 Yo + 0 J  m

Finalmente, o Vector 4 é inclinado 45 º, pois é a diagonal do quadrado, portanto, seus componentes medem o mesmo:

v₄ = -10 Yo + 10 J m

Observe que o sinal -.

O vetor resultante é obtido adicionando componente componente:

v_R = -10 Yo + 10 J m

Então o vetor de equilíbrio do sistema é:

v_E = 10 Yo - 10 J m

Referências

1. Beardon, t. 2011. Uma introdução aos vetores. Recuperado de: nrich.Matemáticas.org.
2. Bedford, 2000. PARA. Mecânica para engenharia: estático. Addison Wesley. 38-52.
3. Figueroa, d. Série: Física para Ciência e Engenharia. Volume 1. Cinemática.31-68.
4. Físico. Módulo 8: vetores. Recuperado de: FRTL.Utn.Edu.ar
5. Hibbeler, R. 2006. Mecânica para engenheiros. Estático. 6ª edição. Empresa editorial continental. 15-53.
6. Vetor da calculadora de adição. Recuperado de: 1728.org
7. Vetores. Recuperado de: Wikibooks.org