Vetores no espaço como representar graficamente, aplicações, exercícios

A vetor no espaço Tudo é representado por um sistema de coordenadas dado por x, e e z. Quase sempre o avião XY É o plano da superfície horizontal e do eixo z representa a altura (ou profundidade).

Os eixos de coordenadas cartesianas mostradas na Figura 1, dividem o espaço em 8 regiões chamadas Ictaves, análogo a como os eixos x - e Divida o avião em 4 quadrantes. Teremos então 1 octante, 2º Ocanto e assim por diante.

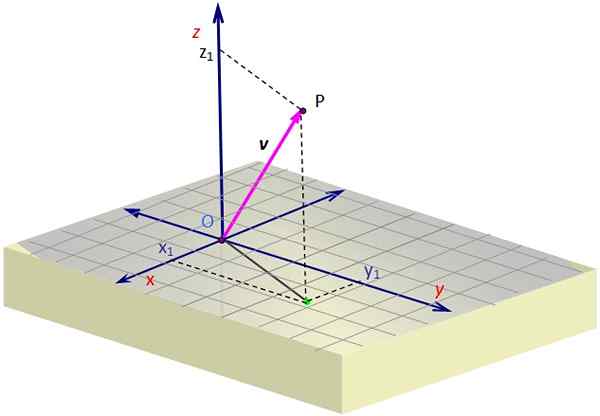
figura 1. Um vetor no espaço. Fonte: Self feito.

A Figura 1 contém uma representação de um vetor v No espaço. É necessária alguma perspectiva para criar a ilusão de três dimensões no plano da tela, o que é alcançado desenhando uma visão oblíqua.

Para representar graficamente um vetor 3D, você deve ajudar as linhas pontilhadas que determinam as coordenadas da projeção ou "sombra" da grade v Sobre a superfície x e. Esta projeção começa em O e termina no ponto verde.

Uma vez lá, você deve continuar na vertical até a altura (ou profundidade) necessária de acordo com o valor de z, Até você chegar a P. O vetor é retirado de O e terminando em P, que no exemplo está no 1º octante.

[TOC]

Formulários

Os vetores no espaço são amplamente utilizados em mecânica e outros ramos da física e da engenharia, uma vez que as estruturas que nos cercam exigem geometria nas três dimensões.

Vetores de posição no espaço são usados ​​para posicionar objetos em relação a um ponto de referência chamado origem QUALQUER. Portanto, eles também são ferramentas necessárias na navegação, mas isso não é tudo.

Pode servir a você: Ondas eletromagnéticas: Teoria Maxwell, Tipos, Características

As forças que atuam em estruturas como parafusos, suportes, cabos, suportes e muito mais são a natureza vetorial e são orientados no espaço. Para saber seu efeito, é necessário conhecer seu endereço (e também seu ponto de aplicação).

E freqüentemente a direção de uma força é conhecida por dois pontos no espaço que pertencem à sua linha de ação. Dessa maneira, a força é:

F = F ou

Onde f é a magnitude ou módulo de força e ou É o vetor da unidade (módulo 1) direcionado ao longo da linha de ação de F. 

Notação e representações vetoriais 3D

Antes de resolver alguns exemplos, a notação de vetores 3D será revisada brevemente.

No exemplo da Figura 1, Vector V, cujo ponto de origem coincide com a origem ou e cujo final é o ponto P, tem coordenadas x e z positivo, enquanto coordena e É negativo. Essas coordenadas são: x₁, e₁, z₁, que são precisamente as coordenadas de P.

Portanto, se tivermos um vetor ligado à origem, ou seja, cujo ponto de partida coincide com O, é muito fácil indicar suas coordenadas, que serão as do ponto extremo ou p. Para distinguir entre um ponto e um vetor, usaremos as mais recentes letras e suportes em negrito, como este:

v = < x₁, e₁, z₁ >

Enquanto o ponto P é indicado com parênteses:

P = (x₁, e₁, z₁)

Outra representação faz uso de vetores de unidade Yo, J e k que definem as três direções do espaço nos eixos x, e e z respectivamente.

Esses vetores são perpendiculares um ao outro e compõem um Base Ortonormal (Veja a Figura 2). Isso significa que um vetor 3D pode ser escrito em termos deles como:

Pode servir a você: movimento ondulado: características, tipos de ondas, exemplos

v = v_x Yo + v_e J + v_z k

Ângulos e diretores de Cosenos de um vetor

A Figura 2 também mostra os ângulos γ dos diretores₁, γ₂ e γ₃ do que o vetor v respectivamente com os eixos x, e e z. Conhecendo esses ângulos e a magnitude do vetor, isso é completamente determinado. Além disso, os cossenos dos diretores cumprem o seguinte relacionamento:

(cos γ₁)² + (cos γ₂)² + (cos γ₃)² = 1

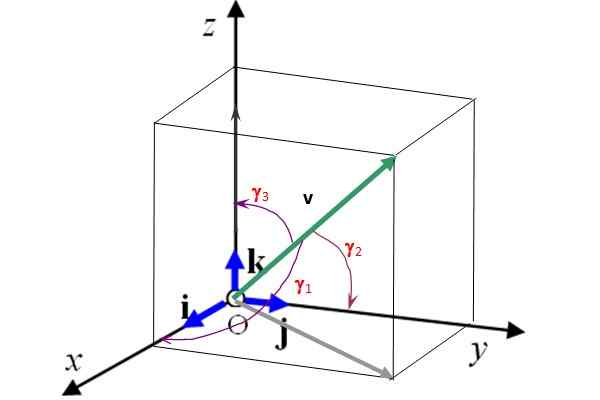Figura 2. Vetores unitários i, j e k determinam as 3 direções preferenciais do espaço. Fonte: Self feito.

Exercícios resolvidos

-Exercício 1

Na Figura 2, os ângulos γ₁, γ₂ e γ₃ do que o vetor v do módulo 50 de forma com os eixos de coordenadas são respectivamente: 75.0º, 60.0º e 34.3º. Encontre os componentes cartesianos deste vetor e represente -o em termos de vetores da unidade Yo, J e k.

Solução

A projeção do vetor v no eixo x é v_x = 50 . Cos 75º = 12.941. Da mesma forma, a projeção de v no eixo e é v_e = 50 cos 60 º = 25 e finalmente no eixo z é v_z = 50. cos 34.3º = 41.3. Agora v pode ser expresso como:

v = 12.9 Yo + 25.0 J + 41.3 k

-Exercício 2 

Encontre tensões em cada um dos cabos que mantêm o balde da figura que está em equilíbrio, se o peso disso for 30 n.

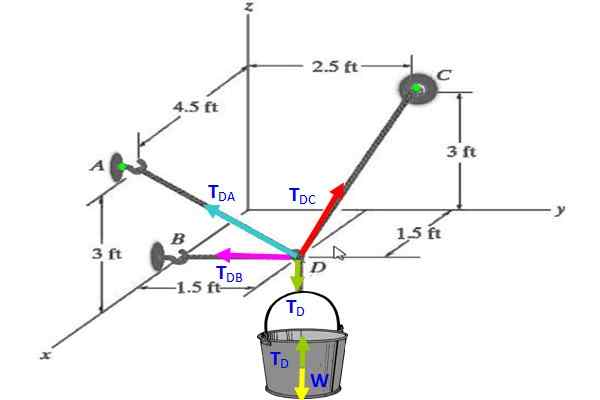Figura 3. Diagrama de tensões para o Exercício 2.

Solução

No balde, o diagrama do corpo livre indica que T_D (verde) compensa o peso C (amarelo), portanto t_D = W = 30 n.

No nó, o vetor T_D  É direcionado verticalmente para baixo, então:

T_D = 30 (-k) N.

Para estabelecer as tensões restantes, você deve seguir as seguintes etapas:

Etapa 1: encontre as coordenadas de todos os pontos

A = (4.5; 0; 3) (A está no avião da parede X-Z)

B = (1.5; 0; 0) (B está no eixo x)

Pode atendê -lo: endereço (físico)

C = (0, 2.5, 3) (C está no plano da parede e z)

D = (1.5; 1.5; 0) (D está no plano horizontal  x e)

Etapa 2: encontre os vetores em cada direção subtraindo as coordenadas do fim e o começo

Dá =

DC =

DB =

Etapa 3: Calcule módulos e vetores de unidade

Um vetor de unidade é obtido por expressão: ou = r / r, com r (em negrito) sendo o vetor e r (sem negrito) o módulo do referido vetor.

Da = (3² + (-1.5)² + 3²)^½ = 4.5; Dc = ((-1.5) ² + 1² + 3²)^½ = 3.5

ou_Dá = 4.5 =

ou_DC = 3.5 =

ou_DB =

ou_D =

Etapa 4: Expresse todas as tensões como vetores

T_Dá = T_Dá ou_Dá = T_Dá

T_DC = T_DC ou_{Dc =}  T_DC

T_DB = T_DB ou_DB = T_DB

 T_D = 30

Etapa 5: aplique a condição de equilíbrio estático e resolva o sistema de equações

Finalmente, a condição de equilíbrio estático é aplicada ao balde, para que a soma vetorial de todas as forças no nó seja anulada:

T_Dá + T_DC + T_DB + T_D = 0

Como as tensões estão no espaço, isso levará a um sistema de três equações para cada componente (x, e e z) de tensões.

0.67 t_Dá -0.43 t_DC + 0 t_DB = 0

-0.33 t_Dá + 0.29 t_DC - T_DB = 0

0.67 t_Dá + 0.86 t_DC +0 t_DB - 30 = 0

A solução é: t_Dá = 14.9 n; T_Dá = 23.3 n; T_DB = 1.82 n

Referências

1. Bedford, 2000. PARA. Mecânica para engenharia: estático. Addison Wesley. 38-52.
2. Figueroa, d. Série: Física para Ciência e Engenharia. Volume 1. Cinemática.31-68.
3. Físico. Módulo 8: vetores. Recuperado de: FRTL.Utn.Edu.ar
4. Hibbeler, R. 2006. Mecânica para engenheiros. Estático. 6ª edição. Empresa editorial continental. 15-53.
5. Vetor da calculadora de adição. Recuperado de: 1728.org