Qual é o vale da física? (Com exemplos)

Ele Vale em física É uma denominação aplicada no estudo de fenômenos ondulados, para indicar o valor mais baixo ou menor de uma onda. Assim, um vale é considerado uma concavidade ou depressão.

No caso da onda circular que é formada na superfície da água quando uma gota ou pedra cai, as depressões são os vales de onda e os inchaços são os cumes.

figura 1. Vales e cumes em uma onda circular. Fonte: Pixabay

Outro exemplo é a onda gerada em uma corda tensa, uma das extremidades é oscilada verticalmente, enquanto o outro permanece fixo. Nesse caso, a onda produzida é propagada com alguma velocidade, possui forma seno e também é constituída por vales e cumes.

Os exemplos anteriores se referem a ondas cruzadas, porque os vales e cumes são transversais ou perpendiculares à direção da propagação.

No entanto, o mesmo conceito pode ser aplicado a ondas longitudinais, como o som no ar, cujas oscilações ocorrem na mesma direção da propagação. Aqui, os vales da onda serão os lugares onde a densidade do ar é mínima e os cumes onde o ar é denso ou comprimido.

[TOC]

Parâmetros de onda

A distância entre dois vales, ou a distância entre dois cumes, é chamada comprimento de onda e denota Com as letras gregas λ. O mesmo ponto de uma onda vai de estar em um vale para ser uma crista à medida que a oscilação se espalha.

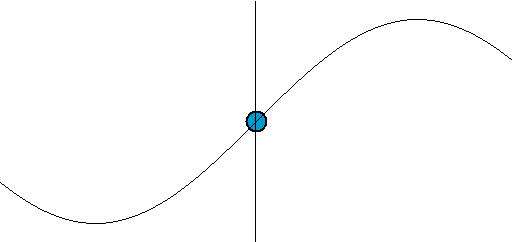Figura 2. Oscilação de uma onda. Fonte: Wikimedia Commons

O tempo que decorre de um valor de vale, estar em uma posição fixa é chamado Período de oscilação E desta vez é indicado com um capital t: T. 

Pode servir a você: Andrômeda: descoberta, origem, características, estrutura

No momento de um período T A onda avança um comprimento de onda λ, É por isso que se diz que o velocidade v com o qual a onda progride é:

V = λ / t

A separação ou distância vertical entre o vale e a crista de uma onda é o dobro da faixa de oscilação, ou seja, a distância de um vale ao centro da oscilação vertical é o amplitude a da onda.

Vales e cumes em uma onda harmônica

Uma onda é harmoniosa se sua forma for descrita pelas funções matemáticas sinusal ou cosseno. Em geral, uma onda harmônica é escrita como:

e (x, t) = um cos (k⋅x ± ω⋅t)

Nesta equação, a variável e representa o desvio ou deslocamento em relação à posição de equilíbrio (y = 0) em posição x No instante t.

O parâmetro PARA É a amplitude da oscilação, uma quantidade sempre positiva que representa o desvio do vale do ondas para o centro de oscilação (y = 0). Em uma onda harmônica, é cumprido que o desvio e, Do vale para a crista, é A/2.

Número da onda 

Outros parâmetros que aparecem na fórmula da onda harmônica, especificamente no argumento da função seno k e frequência angular Ω.

O número da onda k está relacionado ao comprimento de onda λ pela seguinte expressão:

K = 2π/λ

Frequência angular

A frequência angular Ω está relacionado ao período T através:

Ω = 2π/t 

Observe que, no argumento da função sinusal ± ±, ou seja, em alguns casos, o sinal positivo é aplicado e em outros o sinal negativo.

Pode atendê -lo: estático: história, que estudos, aplicações, leis

Se uma onda que se espalha na direção positiva do x, então é o sinal menos (-) que deve ser aplicado. Caso contrário, ou seja, em uma onda que se espalha na direção negativa, o sinal positivo (+) é aplicado.

Onda harmônica

A velocidade de propagação de uma onda harmônica pode ser escrita com base na frequência angular e no número de ondas da seguinte forma:

V = ω/k 

É fácil demonstrar que essa expressão é completamente equivalente à que demos anteriormente, dependendo do comprimento de onda e do período.

Exemplo de vales: a corda do tendard

Uma criança toca as ondas com a corda de um varal de roupas, para o qual desencadeia uma extremidade e a faz oscilada com um movimento vertical a uma taxa de 1 oscilação por segundo.

Durante esse processo, a criança permanece ainda no mesmo lugar e só move o braço de cima para baixo e vice -versa.

Enquanto a criança gera as ondas, seu irmão mais velho tira uma foto com seu celular. Ao comparar o tamanho das ondas com o carro estacionado logo atrás da corda, observe que a separação vertical entre vales e sulcos é a mesma que a altura das janelas do carro (44 cm).

Na foto, também pode ser visto que a separação entre dois vales consecutivos é a mesma entre a borda traseira da porta traseira e a borda frontal da porta da frente (2,6 m).

Função de ondas harmônicas para corda

Com esses dados, o irmão mais velho pretende encontrar a função de onda harmônica, assumindo como um momento inicial (t = 0), o momento em que a mão de seu irmãozinho estava no ponto mais alto. 

Pode servir a você: transferência de calor de radiação (com exemplos)

Isso também significa que o eixo x começa (x = 0) no lugar da mão, com uma direção positiva em direção à frente e passando por metade da oscilação vertical. Com essas informações, você pode calcular os parâmetros da onda harmônica:

A amplitude é metade da altura de um vale para uma crista, isto é:

A = 44cm /2 = 22 cm = 0,22m

O número da onda é 

K = 2π/(2,6 m) = 2,42 rad/m

À medida que a criança levanta e abaixa a mão no tempo de um segundo, então a frequência angular será

Ω = 2π/(1 s) =  6.28 rad/s

Em suma, a fórmula para a onda harmônica é

e (x, t) = 0,22m cos (2.42⋅x - 6.28⋅t)

A velocidade de propagação das ondas será

v = 6.28 rad/s/2.42 rad/m = 15,2 m/s

Posição dos vales na corda

O primeiro vale depois de um segundo de ter iniciado o movimento da mão será a distância d da criança e dada pelo seguinte relacionamento:

e (d, 1s) = -0,22m = 0,22m cos (2.42⋅d - 6.28⋅1)

O que significa que 

cos (2.42⋅d - 6,28) = -1

Quer dizer 

2.42vid. 6,28 = -π 

2.42 progre = π

D = 1,3 m (posição do vale mais próxima de t = 1s)

Referências

1. Giancoli, d. Física. Princípios com aplicações. 6ª edição. Prentice Hall. 80-90
2. Resnick, r. (1999). Físico. Volume 1. Terceira edição em espanhol. México. Empresa Editorial Continental S.PARA. claro.V. 100-120.
3. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Edição. México. Editores de aprendizado do Cengage. 95-100.
4. Cordas, ondas em pé e harmônicos. Recuperado de: newt.Phys.UNSW.Edu.Au

5. Ondas e ondas harmônicas simples mecânicas. Recuperado de: PhysicsKey.com.