Conceito de variação linear, exemplos, exercício resolvido

O Variação linear Ocorre entre duas magnitudes físicas quando o gráfico que as representa é uma linha reta. É equivalente afirmar que as variáveis ​​estão em dependência linear, de modo que, se um deles o chamamos de "y" e o outro "x", eles serão relacionados pela expressão matemática:

y = mx + b

Nesta fórmula, M e B são números reais. O valor de m representa a inclinação ou a inclinação da linha - que é sempre constante - e B é o corte da linha com o eixo vertical.

A variação linear de uma magnitude em relação a outra significa que seu gráfico é uma linha reta. Fonte: Joulesergio/CC BY-S (https: // criativeCommons.Org/licenças/BY-SA/4.0)

Cada fenômeno que responde a uma variação linear tem nomes diferentes para as variáveis, como veremos nos seguintes exemplos. No entanto, a forma matemática da equação é a mesma.

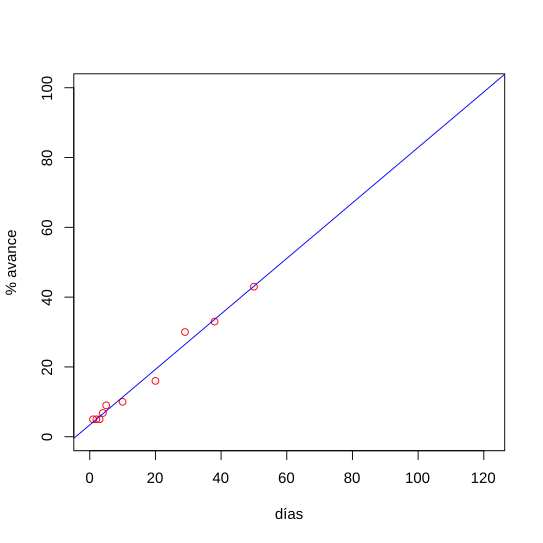
Experimentalmente pode ser estabelecido se houver uma relação linear entre duas magnitudes, medindo casais de valores (x, y).

Os pontos obtidos são gráficos em um artigo de milímetro e são observados se tiverem uma tendência linear, ou seja, se houver uma linha que se ajuste adequadamente aos dados experimentais.

Em primeira instância, essa linha pode ser desenhada visualmente, mas por meio de um regressão linear Eles podem ser encontrados analiticamente, os valores de M e B da linha que melhor se encaixam nos pontos experimentais.

[TOC]

Exemplos de variação linear

Existem numerosos fenômenos naturais, bem como relações estabelecidas entre os padrões de medição, que obedecem a uma variação linear, por exemplo:

Velocidade no movimento retilíneo uniformemente variado

A velocidade dependendo do tempo v (t) de um celular que se move ao longo de uma linha com aceleração constante e velocidade inicial V_qualquer  diferente de 0. Este movimento é conhecido como movimento retilíneo uniformemente variado E a equação de velocidade é:

Pode atendê -lo: densidade

v (t) = V_qualquer + NO

Expansão térmica

Outro fenômeno natural cuja variação é linear é o aumento do comprimento que experimenta uma haste ou um fio quando aquecido.

De fato, quando a temperatura de qualquer objeto aumenta, suas dimensões também, e esse aumento depende da mudança de temperatura ΔT e uma quantidade chamada Coeficiente de dilatação linear denotado pela carta grega α:

L = l_qualquer + α Δt

Nesta expressão L é o comprimento final do objeto e L_qualquer é sua duração inicial.

Posição de um celular com velocidade constante

Um celular com velocidade constante sempre se move em uma linha reta. Se a linha reta for o eixo horizontal x, a posição x (t) a qualquer momento será dada por:

x (t) = x_qualquer + Vt

Onde x_qualquer É a posição inicial, v é a velocidade e t é a hora. Dessa forma, diz -se que a posição X varia linearmente com o tempo t.

Uma estatura de uma pessoa

Médicos e antropólogos podem estimar a estatura de uma pessoa medindo o comprimento do fêmur.

Quanto maior uma pessoa, mais tempo as pernas têm, então existem modelos lineares para prever a altura de uma pessoa adulta H (em polegadas) se o comprimento l (também em polegadas) de seu fêmur for conhecido, de acordo com a equação:

H = 1.880⋅l + 32.010

Escalas de temperatura

As escalas de Celsius e Fahrenheit são usadas diariamente para medir as temperaturas. Esta última escala é comumente usada em países que falam em inglês. Há uma equivalência para passar de um para outro:

F = (9/5) C + 32

Onde f é a temperatura em graus Fahrenheit e C é a temperatura em graus Celsius.

Pressão e profundidade

A pressão absoluta P em um fluido incompressível, como a água, cuja densidade constante é ρ, varia dependendo da profundidade h como:

Pode atendê -lo: tiro horizontal: características, fórmulas e equações, exercícios

P = p_qualquer + ρgh

Onde p_qualquer É a pressão na superfície livre do líquido. Se o líquido estiver em um recipiente aberto à atmosfera, essa pressão é simplesmente a pressão atmosférica p_Atm, Ser capaz de escrever então:

P = p_Atm + ρgh

A pressão atmosférica no nível do mar é de aproximadamente 101 kPa. Essa relação entre P e H significa que a pressão aumenta linearmente com a profundidade.

A pressão experimentada pelo mergulhador varia linearmente com profundidade. Fonte: Ahmed Samy/Pexels.

Exercício resolvido

Custo de direção

O custo mensal C de lidar com um carro inclui um custo fixo mensal C_qualquer Além do custo da milhagem ou da milhagem viajava todos os meses. Um motorista observa que em um mês o custo de gerenciamento era de US $ 380 por US $ 480 e, no mês seguinte, era de US $ 460 por 800 milhas.

Que a quantidade de milhas seja percorrida por mês pelo motorista, com os dados fornecidos, encontre:

a) A variação linear entre C e D.

b) Quanto custaria o carro por mês em uma viagem de 1500 milhas?

c) o gráfico de C versus D.

Solução para

Suponha que as variáveis ​​tenham um relacionamento dado por:

C = c_qualquer + PARA.d

Onde A e C_qualquer Eles são constantes para determinar. A é a inclinação da linha que representa graficamente a relação entre C e D. CO é o corte com o eixo vertical, o custo fixo mensal que o motorista deve pagar pelo mero fato de ter o carro disponível. Aqui, os custos de manutenção e impostos podem ser incluídos, por exemplo.

Para determinar inequivocamente uma linha, é necessário conhecer sua inclinação. Para isso, temos os pontos:

P₁: 480 milhas, US $ 380

P₂: 800 milhas, US $ 460

Esses pontos, de coordenadas (d, c) ou (distância, custo) são análogos aos pontos de coordenadas (x, y) do plano cartesiano, o que muda os nomes. A inclinação da linha é dada por:

Pode atendê -lo: avião inclinado

A = (c₂ - C₁)/(D₂ - d₁)

A = [(460 - 380) $ / (800 - 480) milhas] = (1/4) $ / milha

A inclinação da linha representa o custo por milha, dessa maneira:

C = c_qualquer + PARA.D = co + (1/4).d

Para determinar o custo básico C_qualquer Esta equação é realizada e um dos pontos que conhecemos pertence a ela, por exemplo, P₁:

380 $ = C_qualquer + [(1/4) $ / MILE] . 480 milhas → 380 $ = C_qualquer + $ 120

C_qualquer = $ 260

Agora podemos formular o modelo de variação linear, como:

C = 260 + (1/4) D

Solução b

O custo mensal de viajar 1500 milhas é:

C = 260 + (1/4) x 1500 $ = $ 635

Solução c

O gráfico de C em função de D é:

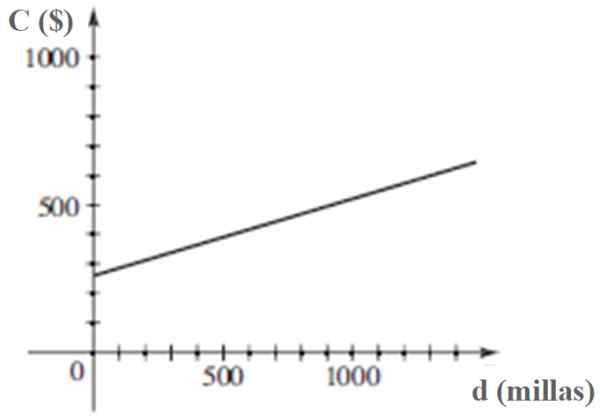O custo c de manuseio de um veículo é uma função linear da distância percorrida D. Fonte: Stewart, J. Pré -cálculo.

Referências

1. Baldor. 1977. Álgebra Elementar. Edições culturais venezuelanas.
2. Hoekenga, c. Equações lineares na ciência. Recuperado de: VisionLearning.com.
3. Hoffman, J. Seleção de questões de matemática. Volume 2.
4. Jiménez, r. 2008. Álgebra. Prentice Hall.
5. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
6. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.