Variáveis ​​estatísticas

O que são variáveis ​​estatísticas?

As Variáveis ​​estatísticas são características que as pessoas, coisas ou lugares possuem e que podem ser medidas. Exemplos de variáveis ​​usadas frequentemente são idade, peso, altura, sexo, status civil, nível acadêmico, temperatura, número de horas que dura uma lâmpada incandescente e muitos outros e muitos outros.

Um dos objetivos da ciência é saber como as variáveis ​​de um sistema se comportam para poder fazer previsões sobre seu comportamento futuro. De acordo com sua natureza, cada variável requer um tratamento específico para obter o máximo de informações.

A quantidade de variáveis ​​para estudar é enorme, mas examinando cuidadosamente o grupo acima mencionado, notamos imediatamente que alguns podem ser expressos numéricos, enquanto outros não.

Isso nos dá a classificação inicial das variáveis ​​estatísticas em dois tipos fundamentais: qualitativa e numérica.

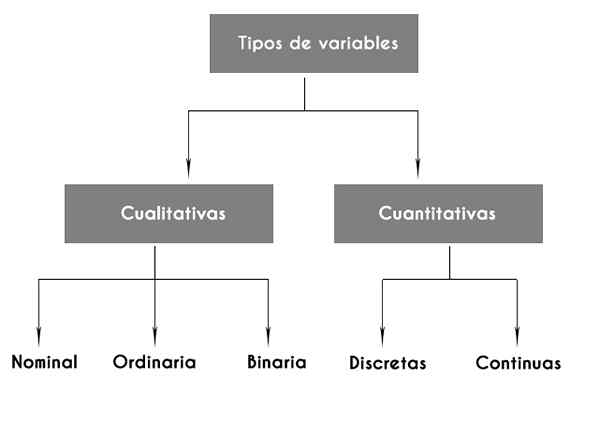
Tipos de variáveis ​​estatísticas

- Variáveis ​​qualitativas

Como o nome indica, variáveis ​​qualitativas são usadas para designar categorias ou qualidades.

Um exemplo bem conhecido desse tipo de variáveis ​​é o status civil: solteiro, casado, divorciado ou viúvo. Nenhuma dessas categorias é maior que a outra, apenas designa uma situação diferente.

Mais variáveis ​​desse tipo são:

-Nível acadêmico

-Ano do ano

-Marca automática que é conduzida

-Profissão

-Nacionalidade

-Países, cidades, distritos, condados e outras divisões territoriais.

Uma categoria também pode ser designada por um número, por exemplo, o número de telefone, o número da casa, a rua ou o código postal, sem isso representando uma avaliação numérica, mas sim um rótulo.

O número da rua é uma variável qualitativa, não é uma variável quantitativa

Variáveis ​​nominais, ordinais e binárias

Variáveis ​​qualitativas podem ser por sua vez:

-Nominal, que atribuem um nome à qualidade, como cor, por exemplo.

-Ordinais, que representam a ordem, como no caso de uma escala de estratos socioeconômicos (alto, médio, baixo) ou opiniões sobre algum tipo de proposta (a favor, indiferente, contra). *

Pode atendê -lo: graus de liberdade: como calculá -los, tipos, exemplos

-Binário, Também chamado dicotômico, Existem apenas dois valores possíveis, como sexo. Essa variável pode receber um rótulo numérico, como 1 e 2, sem representar avaliação numérica ou algum tipo de ordem.

*Alguns autores incluem variáveis ​​ordinais no grupo de variáveis ​​quantitativas, que são descritas abaixo. É porque eles expressam ordem ou hierarquia.

- Variáveis ​​numéricas ou quantitativas

Essas variáveis ​​recebem um número, pois representam quantidades, como salário, idade, distâncias e qualificações obtidas em um exame.

Eles são amplamente utilizados para contrastar preferências e estimar tendências. Eles podem ser associados a variáveis ​​qualitativas e barras de construção e gráficos de histogramas que facilitam a análise visual.

Algumas variáveis ​​numéricas podem ser transformadas em variáveis ​​qualitativas, mas o oposto não é possível. Por exemplo, a variável numérica "idade" pode ser dividida em intervalos com rótulos atribuídos, como bebês, crianças, adolescentes, adultos e idosos.

No entanto, deve -se notar que existem operações que podem ser feitas com variáveis ​​numéricas, que obviamente não podem ser realizadas com as qualitativas, por exemplo, calculando médias e outros estimadores estatísticos.

Se o que você deseja é calcular, você deve manter a variável "idade" como uma variável numérica. Mas outras aplicações podem não exigir detalhes numéricos, pois isso seria suficiente para deixar os rótulos nomeados.

Variáveis ​​numéricas são divididas em duas categorias principais: variáveis ​​discretas e variáveis ​​contínuas.

Variáveis ​​discretas

Las variables discretas únicamente toman ciertos valores y se caracterizan por ser contables, por ejemplo el número de hijos de una familia, la cantidad de mascotas, el número de clientes que visitan a diario una tienda y los suscriptores de una compañía de cable, por mencionar alguns exemplos.

Pode atendê -lo: quadrados mínimos

Definindo, por exemplo, a variável "Número de animais de estimação", leva seus valores do conjunto de números naturais. Uma pessoa pode ter 0, 1, 2, 3 ou mais animais de estimação, mas nunca 2.5 animais de estimação, por exemplo.

No entanto, uma variável discreta necessariamente possui natural ou números inteiros. Os números decimais também servem, uma vez que o critério para determinar se uma variável é discreta é que isso é contabilidade ou numerado.

Por exemplo, suponha que a fração de lâmpadas defeituosas seja definida como uma variável.

Se nenhuma lâmpada estiver com defeito, a variável leva o valor 0. Mas se 1 de n lâmpadas estiver com defeito, a variável vale 1 /n, se houver dois com defeito, é 2 /n e assim por diante até chegar ao evento de que as n lâmpadas estavam com defeito e, nesse caso.

Variáveis ​​contínuas

Ao contrário das variáveis ​​discretas, variáveis ​​contínuas podem aceitar qualquer valor. Por exemplo, o peso dos alunos que estudam um determinado assunto, altura, temperatura, tempo, comprimento e muitos outros outros.

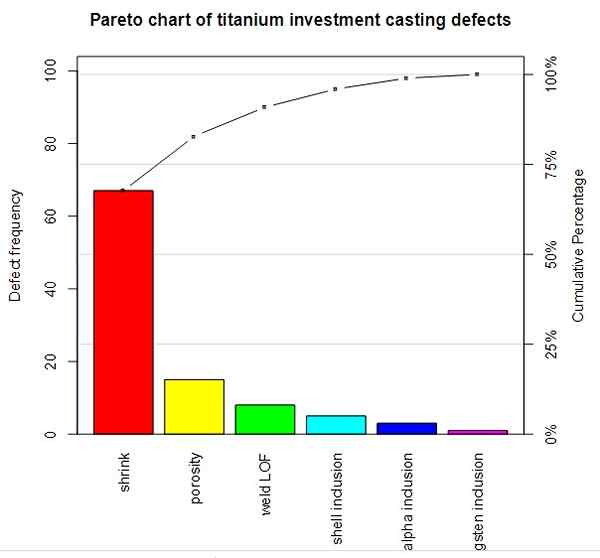Diagrama de Pareto comparando a frequência de defeito (variável quantitativa no eixo vertical) e a porcentagem cumulativa versus cada defeito no eixo horizontal (variável qualitativa). Fonte: Wikimedia Commons.

Como a variável contínua leva valores infinitos, os cálculos de todos os tipos podem ser feitos com a precisão desejada, apenas ajustando o número de decimais.

Na prática, existem variáveis ​​contínuas que podem ser expressas como variáveis ​​discretas, por exemplo, a idade de uma pessoa.

A idade exata de uma pessoa pode ser contada em anos, meses, semanas, dias e mais, dependendo da precisão desejada, mas geralmente rodadas em anos e, assim, se torna discreto.

A renda de uma pessoa também é uma variável contínua, mas geralmente é funcionada melhor se os intervalos forem estabelecidos.

Pode atendê -lo: grau de um polinômio: como é determinado, exemplos e exercícios

- Variáveis ​​dependentes e independentes

As variáveis ​​dependentes são aquelas medidas durante um experimento, para estudar a relação que têm com outras pessoas, o que seria considerado variáveis ​​independentes.

Exemplo 1

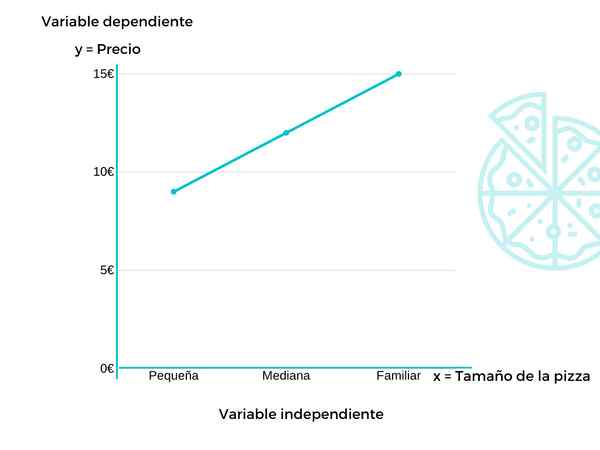
Neste exemplo, veremos a evolução dos preços que sofrem das pizzas de um local de comida, dependendo do seu tamanho.

A variável dependente (y) seria o preço, enquanto a variável independente (x) seria o tamanho. Nesse caso, a pequena pizza vale € 9, a mediana de 12 euros e os € 15 €.

Isto é, à medida que o tamanho da pizza aumenta, custa mais. Portanto, o preço dependeria do tamanho.

Esta função seria y = f (x)

Exemplo 2

Um exemplo simples: você deseja examinar o efeito que as alterações na corrente i produzem através de um fio de metal, para o qual a tensão V é medida entre as extremidades deste.

A variável independente (a causa) é a corrente, enquanto a variável dependente (o efeito) é a tensão, cujo valor depende da corrente que viaja pelo fio.

No experimento, o que é procurado é saber como é a lei quando eu é variado. Se a dependência da tensão com a corrente acabar sendo linear, ou seja: V ∝ I, o motorista é ôhmico e a constante da proporcionalidade é a resistência do fio.

Mas o fato de uma variável ser independente em um experimento não significa que esteja em outro. Isso dependerá do fenômeno em estudo e do tipo de pesquisa que você deseja executar.

Por exemplo, o atual I que viaja um motorista fechado girando em um campo magnético constante, torna -se a variável dependente em relação ao tempo T, que se tornaria a variável independente.

Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
3. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
4. Enciclopédia econômica. Variáveis ​​contínuas. Recuperado de: Encyclopediaeconomica.com.
5. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
6. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.