Qual é a faixa estatística? (Com exemplos)

Ele faixa, Tour ou amplitude, em estatísticas, é a diferença (subtração) entre o valor máximo e o valor mínimo de um conjunto de dados de uma amostra ou população. Se o intervalo com a letra r e os dados forem representados por meio de x, A fórmula para o intervalo é simplesmente:

R = x_máx - x_min

 Onde x_máx É o valor máximo dos dados e x_min É o mínimo.

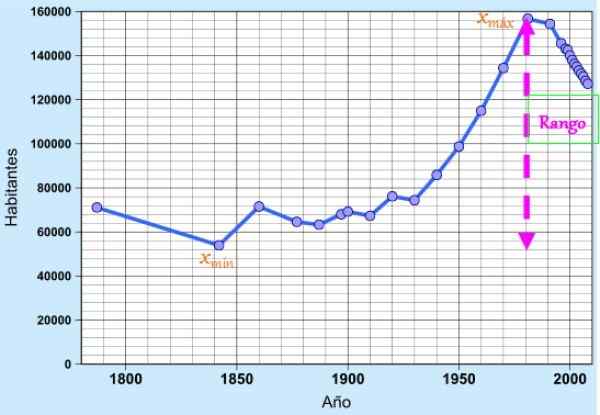
figura 1. Gama de dados correspondentes à população de Cádiz nos últimos dois séculos. Fonte: Wikimedia Commons.

O conceito é muito útil como uma simples medida de dispersão para apreciar rapidamente a variabilidade dos dados, pois indica a extensão ou comprimento do intervalo em que estes são encontrados.

Por exemplo, suponha que a estatura de um grupo de 25 estudantes do sexo masculino do primeiro ano de engenharia em uma universidade. O aluno mais alto do grupo mede 1.93 m e o mais baixo 1.67 m. Esses são os valores extremos dos dados da amostra; portanto, a rota deles é:

R = 1.93 - 1.67 m = 0.26 m ou 26 cm.

A estatura dos alunos deste grupo é distribuída ao longo desta faixa.

[TOC]

Vantagens e desvantagens

O intervalo é, como dissemos antes, uma medida de como os dados são dispersos. Uma pequena faixa indica que os dados são mais ou menos próximos e a dispersão é pequena. Por outro lado, uma faixa maior é indicativa de que os dados são mais dispersos.

As vantagens de calcular o intervalo são evidentes: é muito simples e rápido de encontrar, porque é uma diferença simples.

Ele também possui as mesmas unidades que os dados com os quais funciona e o conceito é muito fácil de interpretar para qualquer observador.

No exemplo da estatura dos estudantes de engenharia, se o intervalo tivesse 5 cm, diríamos que os alunos são todos do mesmo tamanho. Mas com um intervalo de 26 cm, assumimos imediatamente que na amostra há estudantes de todas as estaturas intermediárias. Esta suposição sempre certa?

Pode atendê -lo: diferença entre círculo e circunferência (com exemplos)

Desvantagens do intervalo como medida de dispersão

Se olharmos com cuidado, em nossa amostra de 25 estudantes de engenharia, apenas um deles mede 1.93 e os 24 restantes têm estacionamentos próximos a 1.67 m.

E, no entanto, o alcance permanece o mesmo, embora seja perfeitamente possível que o oposto ocorra: que a estatura da maioria oscila em torno de 1.90 m e apenas um mede 1.67 m.

De qualquer forma, a distribuição dos dados é muito diferente.

As desvantagens do intervalo como medida de dispersão são devidas ao fato de que ela usa apenas valores extremos e ignora todos os outros. Como a maioria das informações é perdida, não há idéia de como os dados da amostra são distribuídos.

Outra característica importante é que o alcance da amostra nunca diminui. Se adicionarmos mais informações, ou seja, consideramos mais dados, o intervalo aumenta ou permanece o mesmo.

E, de qualquer forma, é útil apenas quando trabalha com pequenas amostras, seu uso exclusivo não é recomendado como uma medida de dispersão em amostras grandes.

O que precisa ser feito é complementar com o cálculo de outras medidas de dispersão que levam em consideração as informações fornecidas pelo total de dados: rota Interquartílico, variação, desvio padrão e coeficiente de variação.

Rota interquiril, quartis e exemplo resolvido

Percebemos que a fraqueza do alcance como uma medida de dispersão é que ela utiliza apenas os valores extremos da distribuição dos dados, omitindo os outros.

Para evitar esse inconveniente, o quartis: três valores conhecidos como medidas de posição.

Eles distribuem os dados não agrupados em quatro partes (outras medidas de posição amplamente usadas são o Deciles e os percentis). Essas são suas características:

-O primeiro quartil q₁ É o valor dos dados de modo que 25 % de todos eles sejam menores que q₁.

Pode atendê -lo: proporcionalidade constante: o que é, cálculo, exercícios

-O segundo quartil q₂ É o mediana da distribuição, o que significa que metade (50 %) dos dados é menor que esse valor.

-Finalmente o terceiro quartil q₃ ressalta que 75 % dos dados são menores que q₃.

Em seguida, o intervalo interquotil ou a rota interquartil é definida como a diferença entre o terceiro quartil q₃ e o primeiro quartil q₁ dos dados:

Jornada interquotil = r_Q = Q₃ - Q₁

Dessa forma, o valor da classificação r_Q Não é tão afetado por valores extremos. Portanto, é aconselhável usá -lo quando se trata de distribuições tendenciosas, como alunos muito altos ou muito baixos descritos acima.

- Cálculo de Cuartyles

Existem várias maneiras de calculá -los, aqui vamos propor um, mas em qualquer caso é necessário saber o numero de ordem "N_qualquer”, Que é o lugar que ocupa o respectivo quartil na distribuição.

Isto é, se, por exemplo, o termo correspondente a q₁ é o segundo, terceiro ou quarto e assim por diante.

Primeiro quartil

N_qualquer (Q₁) = (N+1) / 4

Segundo quartil ou mediana

N_qualquer (Q₂) = (N+1) / 2

Terceiro quartil

N_qualquer (Q₃) = 3 (n+1) / 4

Onde n é o número de dados.

A mediana é o valor que está certo no meio da distribuição. Se o número de dados for estranho, não há problema em encontrá -lo, mas se for mesmo, os dois valores centrais são calculados para transformá -los em um em um.

Depois que o número do pedido é calculado, uma dessas três regras é seguida:

-Se você não tiver decimais, os dados indicados na distribuição são procurados e este será o quarto pesquisado.

-Quando o número do pedido está a meio caminho entre dois, os dados indicados por toda a parte com o seguinte fato são calculados em média, e o resultado é o quartil correspondente.

-Em qualquer outro caso, o número inteiro mais próximo é arredondado e esse será o quarto lugar.

Pode atendê -lo: princípio aditivo

Exemplo resolvido

Em uma escala de 0 a 20, um grupo de 16 estudantes de matemática eu obtive as seguintes notas (pontos) em um exame parcial:

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 1, 13, 17, 9, 10, 14

Encontrar:

a) A rota de dados ou dados.

b) os valores dos quartis q₁ e que₃

c) a faixa interquartil.

Figura 2. Faça as qualificações deste exame de matemática faça tanta variabilidade? Fonte: Pixabay.

Solução para

A primeira coisa a fazer para encontrar a rota é ordenar os dados aumentando ou diminuindo. Por exemplo, em ordem crescente que você tem:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Através da fórmula dada no início: r = x_máx - x_min

R = 20 - 1 pontos = 19 pontos.

De acordo com o resultado, essas notas têm uma grande dispersão.

Solução b

N = 16

N_qualquer (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

É um número com decimais, cuja parte inteira é 4. Em seguida, vamos para a distribuição, os dados que ocupa o quarto lugar são procurados e seu valor é calculado com o da quinta posição. Como ambos são 9, a média também é 9 e depois:

Q₁ = 9

Agora repetimos o procedimento para encontrar q₃:

N_qualquer (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Novamente, é um decimal, mas como não está no meio do caminho, é arredondado para 13. O quartil procurado ocupa a treze posição e é:

Q₃ = 16

Solução c

R_Q = Q₃ - Q₁ = 16 - 9 = 7 pontos.

Que, como vemos, é muito menor que o intervalo de dados calculado na seção A), porque a classificação mínima foi 1 ponto, um valor muito mais longe do resto.

Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
3. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
4. Exemplos de quartis. Recuperado de: Mathematics10.líquido.
5. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
6. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.