Fórmula e equações de questões, exemplos, exercícios

O Avaliação Quasiva, A variação quase ou não saudável é uma medida estatística da dispersão dos dados de um amostra Em relação à média. A amostra, por sua vez, consiste em uma série de dados retirados de um universo importante, chamado população.

É indicado de várias maneiras, aqui foi escolhido s_c² E para calculá -lo, a seguinte fórmula segue:

figura 1. A definição de questionário. Fonte: f. Zapata.

Onde:

-s_c ² = A quase

-x_Yo = Cada um dos dados da amostra

-n = número de observações

-X = A média da amostra

Uma vez que a unidade da questionamento da amostra é o quadrado da unidade em que a amostra vem, no momento da interpretação dos resultados, é preferido trabalhar com o Desvio padrão quase ou desvio padrão da amostra.

Isso é indicado como s_c E é obtido extraindo a raiz quadrada da quase -natalidade:

s_c = √ s_c ²

A quaseza é semelhante à variação s², com a única diferença que no denominador disso é N-1, enquanto na variação é dividida apenas por n. É evidente que quando n é muito grande, os valores de ambos tendem a ser os mesmos.

Quando o valor da quase.

[TOC]

Exemplos de questões

Você quer conhecer as características de qualquer população: pessoas, animais, plantas e, em geral. Mas analisar toda a população pode não ser uma tarefa fácil, especialmente se o número de elementos for muito grande.

Em seguida, são coletadas amostras, com a esperança de que seu comportamento reflita a da população e, portanto, seja capaz de fazer inferências sobre isso, graças a quais recursos são otimizados. Isso é conhecido como inferência estatística.

Aqui estão alguns exemplos em que o desvio padrão quase associado a quase associado serve como um indicador estatístico, apontando que os resultados obtidos em relação à média.

Pode servir a você: perímetro do círculo: como retirá -lo e fórmulas, exercícios resolvidos

1.- O diretor de marketing de uma empresa que fabrica baterias de carro precisa estimar, em meses, a duração média da bateria.

Para fazer isso, selecione aleatoriamente uma amostra de 100 baterias dessa marca comprada. A empresa mantém um registro de dados dos compradores e pode entrevistá -los para conhecer a duração das baterias.

Figura 2. Cuasive Appraise é útil para fazer inferências e controle de qualidade. Fonte: Pixabay.

2.- A gestão acadêmica de uma instituição universitária precisa estimar o registro do ano seguinte, analisando o número de estudantes que devem aprovar os assuntos atualmente em.

Por exemplo, de cada uma das seções que atualmente estudam o assunto físico I, o endereço pode selecionar uma amostra de alunos e analisar seu desempenho no referido presidente. Dessa forma, você pode inferir quantos alunos estudarão física II no próximo período.

3.- Um grupo de astrônomos concentra sua atenção em uma parte do céu, onde é observado um certo número de estrelas com certas características: tamanho, massa e temperatura, por exemplo.

Vale a pena perguntar se as estrelas em outra região semelhante terão essas mesmas características, incluindo estrelas em outras galáxias, como as nuvens vizinhas de Magallanes ou Andrômeda.

Por que dividir entre N-1?

Na quaseza, é dividido entre N-1 em vez de n E é porque a quase Estimador insistido, Conforme declarado no começo.

Acontece que da mesma população é possível extrair muitas amostras. A variação de cada uma dessas amostras também pode ser calculada, mas a média dessas variações não é igual à variação da população.

Pode atendê -lo: valor relativo

De fato, a média das variações da amostra tende a subestimar a variação da população, a menos que seja usada N-1 No denominador. Pode -se verificar se o valor esperado da questão e (s_c²) é precisamente².

É por isso que se diz que a quase².

Maneira alternativa de calcular o avaliação quase

É facilmente demonstrado que a quasence também pode ser calculada da seguinte forma:

s_c² = [∑x² / (N -1)] - [∑nx² / (N-1)]

A pontuação padrão

Ao ter o desvio da amostra, podemos saber quantos desvios padrão têm um valor específico x, acima ou abaixo da média.

Para isso, a seguinte expressão sem dimensão é usada:

Pontuação padrão = (x - x) / s_c

Exercício resolvido

Calcule a quase.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Use a definição de questionamento dada no início e também verifique o resultado pela forma alternativa dada na seção anterior.

b) Calcule a pontuação padrão dos segundos dados, lendo de cima para baixo.

Solução para

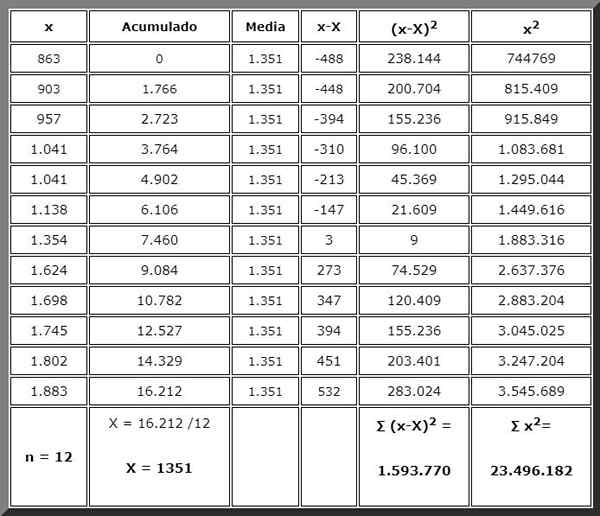
O problema pode ser resolvido manualmente com a ajuda de uma calculadora simples ou científica, para a qual devemos proceder em ordem. E para isso nada melhor do que organizar os dados em uma tabela como a mostrada abaixo:

Graças à tabela que você organizou informações e as quantidades que serão necessárias nas fórmulas estão no final das respectivas colunas, prontas para usar imediatamente. Os sumões são indicados em negrito.

Pode atendê -lo: quais são os 7 elementos da circunferência?

A coluna média é sempre repetida, mas vale a pena, porque é conveniente ter o valor em vista, para preencher cada linha da tabela.

Finalmente, a equação para a quaseza dada no início é aplicada, apenas os valores são substituídos e, em termos da soma, já o calculamos:

s_c² = 1.593.770 / (12-1) = 1.593.770 /11 = 144.888.2

Esse é o valor da quase -fatura e suas unidades são "dólares ao quadrado", o que não faz muito sentido prático; portanto, é calculada as quase as quasidas padrão da amostra, o que nada mais é do que a raiz quadrada da quase -natalidade:

s_c = (√144.888.2) $ = 380,64 $

É imediatamente corroborado que esse valor também é obtido com a forma alternativa da quasence. A soma necessária está no final da última coluna à esquerda:

s_c² = [∑x² / (N-) - [∑nx² / (N-1)] = [23.496.182/11] - [12 x 1351²/ onze]

= 2.136.016.55 - 1.991.128,36 = 144.US $ 888 ao quadrado

É o mesmo valor obtido com a fórmula dada no começo.

Solução b

O segundo valor de cima para baixo é 903, sua pontuação padrão é

Pontuação padrão de 903 = (x - x) / s_c = (903 - 1351)/380.64 = -1.177

Referências

1. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
2. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
3. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
4. Medidas de dispersão. Recuperado de: tales.Cica.é.
5. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.