Medidas de tendência central para fórmulas de dados agrupadas, exercícios

As medidas de tendência central Eles indicam o valor em torno dos quais os dados de uma distribuição são. O mais conhecido é a média média ou aritmética, que consiste em adicionar todos os valores e dividir o resultado pelo número total de dados.

No entanto, se a distribuição consistir em um grande número de valores e não for apresentada de maneira ordenada, não é fácil realizar os cálculos necessários para extrair as informações valiosas que eles contêm.

figura 1. As medidas de tendência central para dados agrupados são um bom indicativo do comportamento geral dos dados

É por isso que eles são agrupados em classes ou categorias, para elaborar um distribuição de Frequências. Realizando esta ordem anterior dos dados, é mais fácil calcular as medidas de tendência central, entre as quais estão:

-Metade

-Mediana

-Moda

-Média geométrica

-Média harmônica

Fórmulas

Abaixo, temos as fórmulas das medidas de tendência central para os dados agrupados:

Média aritmética

A média é a mais usada para caracterizar dados quantitativos (valores numéricos), embora seja bastante sensível aos valores extremos de distribuição. É calculado por:

Com:

-X: aritmética média ou média

-F_Yo: Frequência de classe

-m_Yo: A marca de classe

-G: Número das aulas

-N: Dados totais

Mediana

Para calculá -lo, é necessário encontrar o intervalo que contém a observação N/2 e interpolar para determinar o valor numérico da referida observação, por meio da seguinte fórmula:

Onde:

-C: Largura do intervalo à qual a mediana pertence

-B_M: borda inferior do referido intervalo

-F_m: Número de observações contidas no intervalo

-N/2: Dados totais divididos por 2.

-F_BM: número de observações antes do intervalo que contém a mediana.

Portanto, a mediana é uma medida de posição, ou seja, divide o conjunto de dados em duas partes. Eles também podem ser definidos quartis, Deciles e percentis, que dividem a distribuição em quatro, dez e cem partes, respectivamente.

Pode atendê -lo: Fourier Transform: Propriedades, Aplicações, Exemplos

Moda

Nos dados agrupados, a classe ou categoria que contém a maioria das observações é procurada. Esta é a Classe modal. Uma distribuição pode ter duas ou mais modas, nesse caso, é chamada bimodal e Multimodal, respectivamente.

Você também pode calcular a moda em dados agrupados após a equação:

Com:

-eu₁: Limite inferior da classe onde a moda está

-Δ₁: Permanece entre a frequência da classe modal e a frequência da classe que a precede.

-Δ₂: subtrair entre a frequência da classe modal e a frequência da classe que a segue.

-C: largura de intervalo contendo moda

Média harmônica

A média harmônica é indicada por H. Quando você tem um conjunto de n valores x₁, x₂, x₃…, A média harmoniosa é o inverso ou recíproco da média aritmética do inverso dos valores.

É mais fácil vê -lo através da fórmula:

E ao ter os dados agrupados, a expressão é transformada em:

Onde:

-H: média harmônica

-F_Yo: Frequência de classe

-m_Yo: Marca de classe

-G: Número das aulas

-N = f₁ + F₂ + F₃ +..

Média geométrica

Se você tem n números positivos x₁, x₂, x₃..., sua média geométrica é calculada pelo N-EME do produto de todos os números:

No caso dos dados agrupados, pode -se demonstrar que o logaritmo decimal do log médio geométrico G é dado por:

Onde:

-G: média geométrica

-F_Yo: Frequência de classe

-m_Yo: A marca de classe

-G: Número das aulas

-N = f₁ + F₂ + F₃ +..

Relação entre H, G e X

É sempre verdade que:

H ≤ g ≤ x

Definições mais usadas

As seguintes definições são necessárias para encontrar os valores descritos nas fórmulas anteriores:

Frequência

A frequência é definida como o número de vezes que um fato é repetido.

Faixa

É a diferença entre o valor principal e o menor, presente na distribuição.

Número de classes

Para saber quantas aulas agrupamos os dados, usamos alguns critérios, por exemplo, o seguinte:

Pode atendê -lo: 17 problemas raciocinados

Limites

Os valores extremos de cada classe ou intervalo são chamados limites e cada classe pode ter limites bem definidos, nesse caso, tem um limite inferior e um maior. Ou pode ter limites abertos, quando um intervalo é fornecido, por exemplo de valores, maior ou menor do que um certo número.

Marca de classe

Simplesmente consiste no ponto médio do intervalo e é calculado em média o limite superior e o limite inferior.

Largura do intervalo

Os dados podem ser agrupados em classes de tamanho igual ou diferente, essa é a largura ou amplitude. A primeira opção é a mais usada, pois facilita os cálculos, embora em alguns casos é imperativo que as classes tenham largura diferente.

A largura c A partir do intervalo, pode ser determinado pela seguinte fórmula:

C = intervalo / n_c

Onde_c É o número de classes.

Exercício resolvido

Abaixo, temos uma série de medições de velocidade em km/h, tomadas com radar, que correspondem a 50 carros que passaram por uma rua em uma certa cidade:

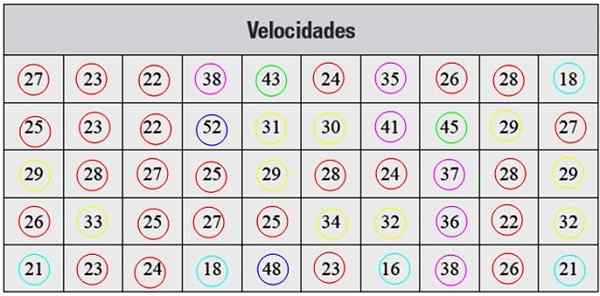Figura 2. Tabela para o exercício resolvido. Fonte: f. Zapata.

Solução

Os dados apresentados não estão organizados, portanto, o primeiro passo é agrupá -los em aulas.

Etapas para agrupar os dados e construir a tabela

Passo 1

Encontre o intervalo R:

R = (52 - 16) km/h = 36 km/h

Passo 2

Selecione o número de classes n_c, De acordo com os critérios fornecidos. Como existem 50 dados, podemos escolher n_c = 6.

etapa 3

Calcule a largura c do intervalo:

C = intervalo /n_c = 36/6 = 6

Passo 4

Classes de formulário e dados do grupo da seguinte forma: Para o primeiro limite inferior da classe A, é escolhido assim que o valor mais baixo presente na tabela é adicionado a esse valor de C = 6, previamente calculado, e é assim obtém o limite superior do primeira classe.

Ele prossegue da mesma maneira para construir o restante das classes, como mostrado na tabela a seguir:

Pode atendê -lo: o que é um número Capicúa? Propriedades e exemplos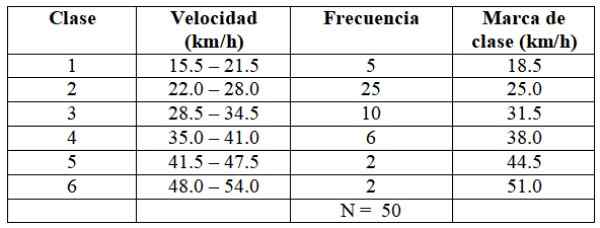

Cada frequência corresponde a uma cor na Figura 2, assim é garantido que nenhum valor escape de ser contabilizado.

Cálculo médio

X = (5 x 18.5 +25 x 25.0 + 10 x 31.5 + 6 x 38.0 + 2 x 44.5 + 2 x 51.0) ÷ 50 = 29.03 km/h

Cálculo mediano

A mediana está na classe 2 da tabela, pois existem os 30 primeiros dados de distribuição.

-Largura do intervalo à qual a mediana pertence: c = 6

-Borda inferior do intervalo onde está a mediana: b_M = 22.0 km/h

-Número de observações contidas no intervalo f_m = 25

-Dados totais divididos por 2: 50/2 = 25

-Número de observações antes do intervalo que contém a mediana: f_BM = 5

E a operação é:

Mediana = 22.0 + [(25-5) ÷ 25] × 6 = 26.80 km/h

Moda

A moda também é encontrada na classe 2:

-Largura do intervalo: C = 6

-Limite inferior da classe onde a moda é encontrada: l₁ = 22.0

-Subtrair entre a frequência da classe modal e a frequência da classe que a precede: δ₁ = 25-5 = 20

-Subtrair entre a frequência da classe modal e a frequência da classe a seguir: δ₂ = 25 - 10 = 15

Com estes dados, a operação é:

Moda = 22.0 + [20 ÷ (20 + 15)] x6 = 25.4 km/h

Cálculo da média geométrica

N = f₁ + F₂ + F₃ +... = 50

log g = (5 x log 18.5 + 25 x log 25 + 10 x log 31.5 + 6 x log 38 + 2 × log 44.5 + 2 x log 51) /50 =

log g = 1.44916053

G = 28.13 km/h

Cálculo médio harmônico

1/h = (1/50) x [(5/18.5) + (25/25) + (10/31.5) + (6/38) + (2/44.5) + (2/51)] = 0.0366

H = 27.32 km/h

Resumo das medidas de tendência central

As unidades de variáveis ​​são km/h:

-Mídia: 29.03

-Mediana: 26.80

-Moda: 25.40

-Mídia geométrica: 28.13

-Média harmônica: 27.32

Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
3. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
4. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
5. Spiegel, m. 2009. Estatisticas. Série Schaum. 4 ta. Edição. McGraw Hill.
6. Tratamento de dados agrupados. Recuperado de: Itchihuahua.Edu.mx.
7. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.