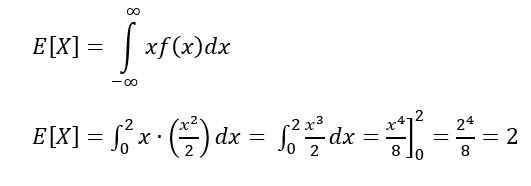Variável aleatória contínua

Explicamos que variável aleatória contínua, suas características, exemplos e um exercício resolvido é

O que é uma variável aleatória contínua?

A Variável aleatória contínua É um valor numérico obtido aleatoriamente, o que resulta de fazer um experimento e pode levar valores infinitos. Isso significa que, conhecidos dois valores consecutivos da variável, é sempre possível encontrar outro valor intermediário entre eles.

Por ter uma quantidade infinita de valores, a coleta de valores variáveis ​​contínuos não é contábil e quase sempre pertence ao conjunto de números reais.

Exemplos desse tipo de variáveis ​​são a estatura, o peso e a temperatura corporal de uma pessoa, mas inúmeros deles podem ser definidos, vários exemplos serão encontrados abaixo. Em contraste com a variável aleatória contínua, há a variável aleatória discreta, que é contabilidade, como o número de filhas em uma família ou quantos carros uma agência vende após um mês.

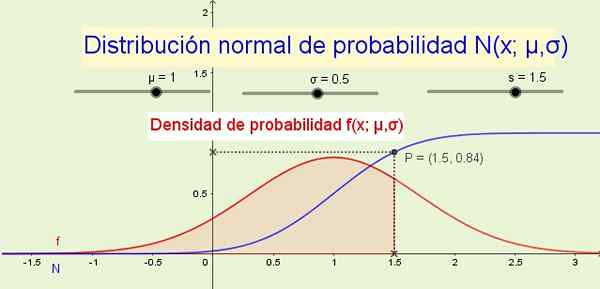
Variáveis ​​aleatórias discretas frequentemente seguem a distribuição de probabilidade normal. Fonte: f. Zapata.

Uma variável aleatória contínua é indicada por meio de uma letra maiúscula como o X, e os valores infinitos que a variável leva são os possíveis resultados do experimento aleatório:

X = x₁, x₂, x₃,… ∞

Cada valor tem uma certa probabilidade de ocorrência e para o modelo pelo qual essa probabilidade é calculada, é chamado distribuição de probabilidade.

Mas, como X assume valores infinitos, a probabilidade de valores específicos da variável não pode ser calculada. Portanto, é necessário definir uma função f (x), chamada Função de distribuição acumulada, ou simplesmente função de distribuição, segundo a qual a probabilidade acumulada é calculada para um determinado valor ou entre dois valores:

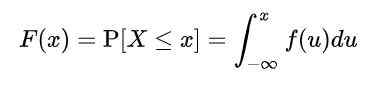
Onde f (u) receber o nome de Função de densidade. Definido dessa maneira, F (x) representa a probabilidade de que X está entre -∞ e x.

Características de uma variável aleatória contínua

As variáveis ​​aleatórias contínuas estão completas f (x).

A função de densidade f (x) Deve atender às seguintes propriedades:

• A função f (x) É positivo: f (x)> = 0
• A área sob a curva y = f (x) É sempre igual a 1, ou seja, a probabilidade de ocorrência de algum resultado x No intervalo (-∞, +∞) é 100%.
• A probabilidade de X estar no intervalo [a, b] é calculada pela seguinte integral definida:

Pode servir a você: Curtose: Definição, Tipos, Fórmulas, para que é, por exemplo,

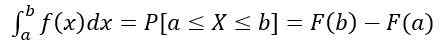
Que é equivalente à área sob a curva y = f (x), entendido entre para e b. Além do mais:

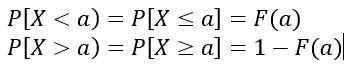
Os valores de f (x) Eles não representam uma probabilidade, então P [x = c] = 0. Os valores relevantes são aqueles correspondentes à área sob a curva y = f (x), que representam uma probabilidade.

• Derivando a função de distribuição F (x) em relação a x, se obtem f (x).

O gráfico de f (x) Para uma variável aleatória contínua, é análogo ao polígono de frequência que é construído para uma variável estatística discreta, com a diferença de que, para a variável aleatória, a largura do intervalo se torna infinitesimal.

Ter esperança

A esperança é uma das medidas características de uma variável contínua. A esperança ou o valor esperado de X Indica o valor que deve ocorrer com mais frequência e é calculado através da seguinte integral:

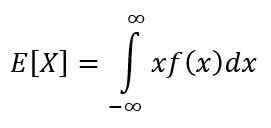
Suas propriedades são:

• E [a∙ X] = A∙ e [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ X+B∙ Y] = A∙ e [x] + b∙ e [y]

Onde os valores para e b Eles são números reais.

Exemplos

Como indicado anteriormente, existem muitas situações em que uma ou mais variáveis ​​aleatórias contínuas podem ser definidas. Nas ciências e outras áreas, as mais comuns são de tempo, comprimento, peso, volume e temperatura:

Tempo

Para otimizar processos e serviços, são projetados experimentos que estudam o tempo que eles levam para serem realizados:

X = tempo que leva um cliente para a janela do banco.

Y = o que ocupa um local de fast food em servir um pedido.

Z = tempo em que uma certa reação química ocorre.

Estaturas e pesos

Em muitos estudos sobre pessoas e animais, estaturas e pesos são relevantes:

X = altura das meninas em um 6º curso. Diploma em cada escola em uma cidade.

Pode servir a você: congruência: figuras congruentes, critérios, exemplos, exercícios

Y = peso de bebês no nascimento em um hospital público.

Z = o peso das vacas em uma fazenda.

Temperaturas

A temperatura é um parâmetro relevante em vários processos químicos, que geralmente leva valores infinitos em um determinado intervalo:

X = temperatura na qual ocorre uma certa reação química, sabendo que isso ocorre entre 80 ºC e 120 ºC.

Exercícios resolvidos

Exercício 1

Determine quais são as variáveis ​​aleatórias contínuas:

1. O número de estudantes que frequentam o café da universidade ao dia.
2. Pressão arterial de pacientes que chegam a uma sala de emergência.
3. Comprimento das asas de pássaros, de uma espécie ameaçada, que habita uma reserva.
4. O tempo entre uma pessoa e outra é tratado em um banco.
5. Quantidade de produtos defeituosos por mês em uma fábrica.
6. Níveis de colesterol nas galinhas de uma fazenda.
7. Quantidade de lâmpadas de rua em uma rua, de um total de 12.

Solução

1.- O número de estudantes atendidos ao dia é entorável, portanto, essa variável não é contínua, mas discreta.

2.- É contínuo. A pressão arterial dos pacientes pode assumir qualquer valor em um determinado intervalo.

3.- Variável contínua, uma vez que o comprimento da asa de um pássaro leva qualquer valor entre um mínimo e um máximo, dependendo da espécie.

4.- O tempo entre o atendimento ao cliente é variável e pode assumir qualquer valor em um determinado intervalo, por exemplo, entre 1 e 5 minutos.

5.- Como o número de produtos defeituosos é contábil, é uma variável aleatória discreta.

6.- Essa variável é contínua, uma vez que o nível de colesterol nas galinhas assume qualquer valor em um intervalo previamente determinado.

Pode servir a você: ângulos complementares: qual e como eles são calculados, exemplos, exercícios

7.- Discreto. O número de luzes de iluminação que o trabalho é um valor contábil.

Exercício 2

A variável aleatória contínua é definida X ""nível de colesterol " Em uma certa variedade de galinhas de uma fazenda, que tem a seguinte função de densidade f (x):

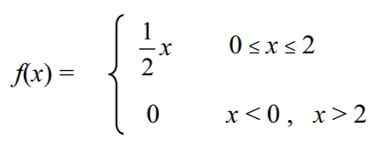
Calcule o seguinte:

1. F (x)
2. P [x ≤2]
3. A esperança EX]

Solução para

De acordo com a definição dada no início:

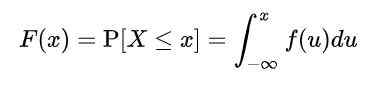
Portanto, F (x) É uma função em partes. Para o intervalo x<0, F (x) É igual a 0, pois as propriedades declaradas no começo.

No intervalo 0≤x≤2, A integral indefinida é resolvida:

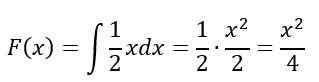
Finalmente, para o intervalo x> 2, F (x) = 1, De acordo com as propriedades, portanto, F (x) Permanece assim:

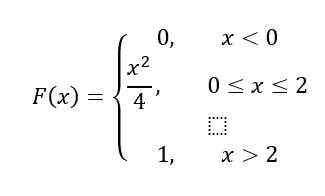
Solução b

A probabilidade procurada é F (1.2) e COmo x = 1.2 É encontrado entre 0≤x≤2, essa parte de F (x) para avaliar:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Solução c

Para calcular a esperança ou o valor esperado, é usado: