Testando hipóteses

O que é o teste de hipótese?

O testando hipóteses, Nas estatísticas, é um procedimento usado para verificar como é bem -sucedido uma conjectura sobre um população. Essas conjecturas são chamadas hipótese, que em princípio eles são considerados verdadeiros, até que algumas evidências confirmem ou neguem.

Esta evidência é fornecida por dados de amostra, aqueles que vêm de uma parte significativa da população, chamada amostra. A teoria das probabilidades fornece as técnicas necessárias para contrastar a veracidade das hipóteses.

Exemplos de hipóteses são:

-A temperatura corporal humana média é 36.1 ºC.

-Em média, uma bolsa de amendoim salgada produzida em uma fábrica de lanches pesa 50 g.

-80% dos habitantes de uma cidade fizeram compras on -line nos últimos 6 meses.

-Pontuações de teste de QI para estudantes universitários de uma instituição bem conhecida, tem um desvio padrão de 15.

-Uma certa variável aleatória x segue uma distribuição de Poisson.

Os quatro primeiros são do tipo de hipótese paramétrico, Porque essas são declarações sobre algum parâmetro populacional, como média, desvio padrão ou alguma proporção.

Por outro lado, a última hipótese estabelece a distribuição de uma variável aleatória e, como não se refere a nenhum parâmetro ou propriedade da população, diz -se que é uma hipótese não paramétrico.

Hipótese nula e hipótese alternativa

Existem dois tipos de hipótese com a qual realizar um teste, que servirá para contrastá -los:

-Hipótese nula, indicado como h₀, afirma que o parâmetro em estudo tem um valor estabelecido ou que a variável aleatória segue uma certa distribuição. Portanto, ao expressar simbolicamente a hipótese nula, o símbolo da igualdade é sempre usado.

-Hipótese alternativa: chamado h₁, Ele afirma que o parâmetro ou distribuição são diferentes do que a hipótese nula garante, portanto, para expressar simbolicamente a hipótese alternativa, os símbolos são usados: ou ≠, mas nunca igualdade.

Pode servir a você: propriedade da Bloqueio de Álgebra: Demonstração, Exemplos

Quando a hipótese nula é aceita, a hipótese alternativa é rejeitada, de modo que ambos são mutuamente exclusivos.

Nível de significância

É uma medida para o erro que pode ser cometido ao realizar um teste de hipótese. É definido como a probabilidade de rejeitar a hipótese nula, sendo que é verdade. Geralmente é indicado com a carta grega α:

α = p (rejeição H₀ Quando é verdade)

Os valores comumente usados ​​para α são 0.01, 0.05 e 0.10; sendo o segundo o uso mais frequente. Equivalente, respectivamente, a 1%, 5% e 10% de probabilidade de cometer erros ao rejeitar H₀, Mas, de qualquer forma, quanto menor o nível de significância, mais confiável o resultado do teste.

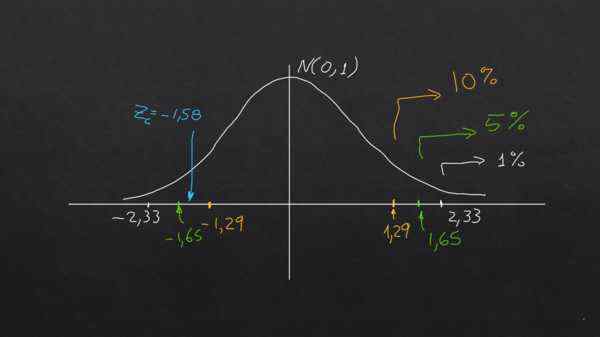
O valor alfa (α) pode ser entendido como a fração percentual da área da cauda direita (ou esquerda), em uma distribuição normal tipificada (μ = 0 e σ = 1) e esses valores sempre ocorrem em z = 2,33 para α = 0.01; em z = 1,65 para α = 1,65 e em z = 1,29 para α = 0,1.

Etapas para realizar um teste de hipótese

Passo 1

Defina respectivamente as hipóteses nulas e alternativas. A hipótese nula estabelece que o parâmetro em estudo, chamado θ, é igual a um valor de referência, indicado como θ₀:

H₀: θ = θ₀

Por exemplo, se os efeitos de um medicamento forem investigados em uma certa característica de uma população de camundongos laboratoriais, a hipótese nula contempla de que esse medicamento não faz nenhuma diferença nessa característica e que isso tem um valor constante θ₀.

Para simbolizar a hipótese nula, o sinal de igualdade é sempre usado, por outro lado, a hipótese alternativa faz uso de um dos símbolos ou ≠.

No exemplo do medicamento, a hipótese alternativa estabelece que o composto tem algum efeito na característica em questão. Portanto, isso é maior, mais baixo ou simplesmente diferente do valor de referência θ₀.

Pode atendê -lo: notação fatorial: conceito, exemplos e exercícios

Passo 2

Escolha o nível de significância apropriado, que geralmente é estabelecido em 5 %, como indicado anteriormente.

etapa 3

Determine a população e o extrair a amostra, ou amostras, cuja análise servirá para contrastar as hipóteses e determinar a aceitação ou rejeição da hipótese nula.

Passo 4

Escolha e calcule o valor da estatística do estudo para os dados coletados, dos quais a evidência necessária é obtida para tomar a decisão de aceitar ou rejeitar a hipótese nula. A escolha da estatística do estudo depende do parâmetro selecionado: média, desvio, proporção ou outro.

A estatística do estudo é obtida convertendo um parâmetro de amostra em uma pontuação z, um aluno, r pérola ou estatística quadrada chi, de acordo com o projeto experimental selecionado. Existem fórmulas para isso.

Geralmente, se o parâmetro populacional for o μ médio, “x bar” é a média da amostra, o desvio padrão σ é conhecido e o tamanho da amostra é n> 30, a estatística de teste z_C É calculado com a pontuação z:

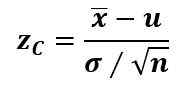
E quando n < 30, pero σ es desconocida, se usa la t de Student.

Etapa 5

Estabeleça critérios para aceitação ou rejeição da hipótese nula, que pode ser feita através de dois procedimentos:

• Através dos valores de P.
• Em comparação com valores críticos.

Os valores de p são equivalentes à probabilidade de obter os resultados encontrados, uma vez que a hipótese nula é verdadeira. Se esses valores forem pequenos, a hipótese nula é rejeitada, se não forem, é aceita. De qualquer forma, os valores de P não constituem a prova de que a hipótese alternativa é verdadeira.

Deve -se levar em consideração que, em um teste de hipótese, é possível cometer dois tipos de erro:

• Erro do tipo I: Rejeitar h₀ Quando é verdade. Sua probabilidade é α e é equivalente ao nível de significado de prova.
• Erro do tipo II: Aceitar h₀ Quando é realmente falso. Sua probabilidade é indicada como β.

Pode atendê -lo: qual é a relação entre a área de Rhombus e o retângulo?

Etapa 6

Tome a decisão de aceitar ou rejeitar a hipótese nula. Se os valores de p forem usados, quando p < α, se rechaza H₀ E H é aceito₁, E caso contrário, H é aceito₀. O conjunto de valores de P < α se conoce como região crítica. Se a estatística estiver nesse intervalo, h é rejeitado₀.

Da mesma forma, um valor crítico é selecionado, de acordo com o parâmetro populacional escolhido. Se esta for a média, prossiga da seguinte maneira:

• Teste de uma cauda: θ < θ₀ ou θ> θ₀
• Teste de duas caudas: | θ | < θ₀

Exemplo resolvido

Uma máquina fabrica parafusos cujo valor nominal deve ter 800 milímetros de comprimento, com um desvio padrão de 5%.

Uma amostra aleatória é coletada, ou seja, em diferentes dias da semana de produção, que totaliza cerca de 40 parafusos. Quando o comprimento médio da amostra é calculado, o valor de 790 milímetros é obtido.

Determine se o comprimento médio está em tolerância com níveis de significância, respectivamente, de 1%, 5% e 10%.

Solução

O primeiro é calcular a estatística média de teste, que neste caso é o desvio da média dividida entre o erro da população padrão:

ZC = (790 - 800) / (40 / √40) = -1,58

Onde foi levado em consideração que 5% desvios padrão corresponde a 40 de 800.

A hipótese nula é que a amostra média está dentro da tolerância permitida ao nível de significância necessário, desde que | ZC | é menor que o valor tipificado | zt |, caso contrário, a hipótese nula é rejeitada.

Para significância de 1% e 5%, a hipótese nula é atendida, pois | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

No entanto, para 10% de significado, acontece que | ZC | > 1,29. Isto é, nesse nível de significância, a hipótese nula não é atendida.

O gráfico a seguir esclarece a conclusão:

O gráfico mostra como dependendo do nível de significância exigido, a mesma hipótese pode ser aceita ou rejeitada com os mesmos dados. Fonte: f. Zapata.