Estimativa por intervalos

Qual é a estimativa por intervalos?

O Estimativa por intervalos É a maneira de determinar o intervalo de valores nos quais a média da população pode ser incluída, com base nas informações de uma amostra de tamanho finito, extraído aleatoriamente da população total.

Ele Intervalo de estimativa É menor, pois a amostra é maior, mas se torna mais ampla se o nível ou porcentagem de confiabilidade dos mesmos aumentar.

Se você deseja saber a média populacional de uma certa variável na forma exata, a população total deve ser considerada, algo que nem sempre é viável, pois se for uma população muito grande, é caro obter os dados do População inteira. Por esse motivo, uma ou mais amostras aleatórias da população total são usadas para tomar.

É baseado na hipótese de que, extraindo uma amostra aleatória, não tendenciosa e levando em consideração proporcionalmente todos os estratos, o valor médio da amostra deve estar muito próximo do da média da população.

A lógica indica que quanto maior os dados da amostra, a diferença entre o valor médio da amostra e o valor médio da população é menor.

Intervalo de estimativa

Na prática, a menos que a população completa seja conhecida, só é possível encontrar, com alguma probabilidade, o intervalo em que a média da população pode ser encontrada, com base em uma amostra de tamanho finito.

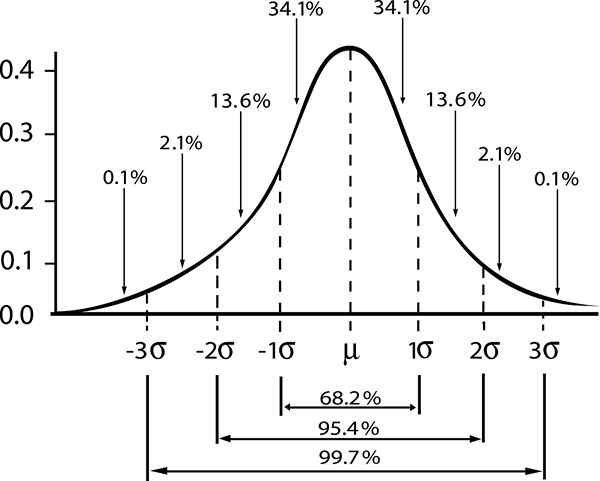
No caso de uma população que segue uma distribuição normal, com Desvio padrão σ , o Diferença padrão Entre a média da população μ e a amostra média de tamanho n É dado por:

| μ - | ≤ σ / √n

Aqui, a palavra "padrão" indica que 68% das amostras de tamanho n, Eles têm valor médio entre o intervalo [μ - σ / √n, μ + σ / √n].

Pode atendê -lo: critérios de divisibilidade: quais são eles, quais são o uso e as regras

Estimativa padrão

Uma interpretação alternativa do exposto acima seria dizer que a população média obtida de uma amostra de tamanho n e o valor médio é entendido no intervalo  [ - σ / √n, + σ / √n], Com 68% de probabilidade.

Na maioria dos casos reais, não é possível conhecer o desvio populacional padrão, então σ É aproximado pelo desvio padrão da amostra s, que é calculado da seguinte forma:

S = √ (∑ (x_Yo - )² / √ (n-1).

A partir daí, você obtém o intervalo que pode conter a população significa com um nível de confiança de 68% (nível de confiança padrão), dado por:

  -s / √n ≤ μ ≤ + s / √n

Este intervalo de medição populacional é conhecido como intervalo de estimativa padrão e foi obtido apenas com os dados disponíveis em tamanho n.

A partir da fórmula anterior, segue -se que, se você quiser fortalecer o intervalo de estimativa pela metade, é necessário quadruplicar O tamanho da amostra.

Estimativa por intervalos de confiança

Em certos estudos, um nível padrão de 68% pode ser insuficiente, então é necessário determinar os intervalos com um nível de confiança arbitrário γ.

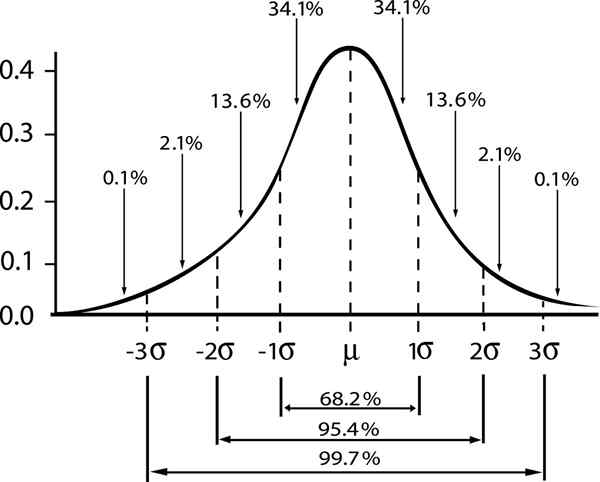A relação entre a margem de confiabilidade e o intervalo em uma distribuição gaussiana é mostrada

Se denotarmos por ε O erro padrão s/√n, então o erro da estimativa para um nível de confiança γ será dado por:

E = zγ⋅ε.

Onde Zγ É um número pelo qual o erro padrão é multiplicado e, assim, obtenha a margem de erro com um nível de confiança arbitrário γ.

Para obter o fator Zγ, proceda da seguinte forma:

Pode atendê -lo: números racionais: propriedades, exemplos e operações

Passo 1

É a chamada nível de significância α correspondente ao nível de confiança γ Pela fórmula a seguir:

α = 1 - γ

Passo 2

O valor é determinado:

Esta é a frequência acumulada em uma distribuição normal tipificada N (0,1) No intervalo (-∞, Zγ ].

etapa 3

Isso limpa Zγ A equação:

N (zγ) = 1 - α/2

Como é uma equação integral, essa folga é obtida nas tabelas de distribuição normal, usando o método de interpolação linear.

Passo 4

Alternativamente ao uso de tabelas, as funções estatísticas incorporadas nas planilhas como Excel, qualquer Folha do Google. Esses programas incorporam função inversa normal N^-1, para que o fator de correção Zγ É obtido avaliando diretamente esta função inversa:

Zγ = n^-1(1 - α/2).

Intervalos de confiança típicos

Os níveis de confiança mais usados ​​são:

• Zγ = 1; nível de confiança padrão γ = 0,68.
• Zγ = 2; nível de confiança γ = 0,95 (ou nível de significância 5%).
• Zγ = 3; nível de confiança γ = 0,997 (ou nível de significância 0,3%)

Exemplos

Exemplo 1

Determine o intervalo médio de peso dos recém -nascidos durante o mês de agosto em uma grande cidade com base em uma amostra aleatória de 100 bebês, na qual um peso médio de 3100 gramas foi obtido com um desvio padrão de amostra S = 1500 gramas.

Solução

Primeiro, o erro padrão da amostra é determinado:

ε = s/√n = (1500 g)/√100 = 150 g.

Portanto, a partir desta amostra, pode -se inferir que o peso médio dos bebês nascidos em agosto naquela cidade está entre 2950 g e 3250 g, com 68% de probabilidade.

Exemplo 2

Suponha que o tamanho da amostra de bebês nascidos no mesmo mês de agosto e na mesma cidade do Exemplo 1. O peso médio da amostra é de 3100 g com uma dispersão padrão de 1500 g. 

Pode servir a você: Decomposição de números naturais (exemplos e exercícios)

É solicitado a estimar o intervalo médio de peso dos recém -nascidos daquela cidade, a partir desta nova amostra.

Solução

Agora o erro padrão diminui no fator 1//√2, Portanto, o novo erro padrão do peso médio será de 106 g.

Em seguida, pode -se estimar, a partir desta nova amostra que, o peso médio dos recém -nascidos é composto na faixa de 2994 g a 3206 g, com uma probabilidade de 68%.

Exercícios

Exercício 1

Determine a faixa média de peso de recém -nascidos em agosto, a partir da amostra especificada no Exemplo 1, com uma probabilidade de 95%.

Solução

Um nível de confiabilidade de 95% dobra a faixa média de peso, em comparação com um nível de confiabilidade de 68%.

Portanto, o peso médio dos recém -nascidos está incluído na faixa de 2800 gramas a 3400 gramas com 95% de certeza.

Exercício 2

Estime com um nível de confiança de 99,7% no intervalo em que o peso médio dos recém -nascidos de uma cidade grande será encontrado, se houver uma amostra disponível com o peso médio de 100 bebês igual a 3100 g e com um desvio de amostra padrão S = 1500 g.

Solução

A margem média de erro de peso, com 99,7% da certeza, será triplamente o erro médio, ou seja::

3*1500/√100.

Em seguida, é inferido, a partir desta amostra, que o peso médio que os recém -nascidos serão incluídos no intervalo: 2650 gramas a 3550 gramas, com um nível de certeza de 99,7%. 

A partir deste resultado, é observado como um nível maior de certeza aumenta a incerteza do peso médio para um intervalo muito mais amplo.