Erro percentual
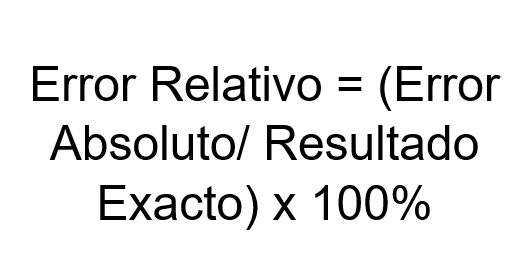
- 5060
- 1609
- Conrad Schmidt
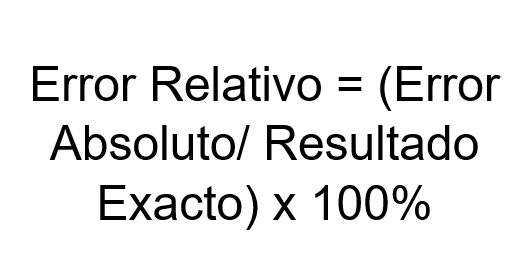
Qual é o erro percentual?
Ele erro percentual É a manifestação de um erro relativo em termos percentuais. Em outras palavras, é um erro numérico expresso pelo valor que dá um erro relativo, subsequentemente multiplicado por 100.
Para entender o que é um erro percentual, você deve primeiro entender que erro numérico, um erro absoluto e um erro relativo, uma vez que o erro percentual é derivado desses dois termos.
Um erro numérico é aquele que aparece quando uma medida é tomada equivocamente ao usar um dispositivo (medição direta) ou quando uma fórmula matemática (medida indireta) é mal aplicada.
Todos os erros numéricos podem ser expressos absolutamente ou porcentagem. Por sua parte, o erro absoluto é aquele que ocorre ao executar uma abordagem para representar uma quantidade matemática resultante da medição de um elemento ou da aplicação errônea de uma fórmula.
Dessa forma, o valor matemático exato é alterado pela abordagem. O cálculo do erro absoluto é realizado subtraindo a abordagem ao valor matemático exato, como este:
Erro absoluto = resultado exato - abordagem
As unidades de medida usadas para manifestar o erro relativo são as mesmas que são usadas para falar sobre o erro numérico. Da mesma forma, esse erro pode dar um valor positivo ou negativo.
O erro relativo é o quociente obtido dividindo o erro absoluto pelo valor matemático exato.
Dessa maneira, o erro percentual é o que é obtido multiplicando o resultado do erro relativo por 100. Em outras palavras, o erro percentual é a expressão percentual (%) do erro relativo.
Pode atendê -lo: x quadradoErro relativo = (erro absoluto/ resultado exato)
Um valor percentual que pode ser negativo ou positivo, ou seja, pode ser um valor representado por excesso ou padrão. Esse valor, diferentemente do erro absoluto, não apresenta unidades além das do percentual (%).
Erro relativo = (erro absoluto/ resultado exato) x 100%
A missão de erros relativos e percentuais é indicar a qualidade de algo ou fornecer valor comparativo.
Exemplos de cálculo do erro percentual
1. Medição de duas terras
Ao medir dois lotes ou terras, diz -se que há aproximadamente 1 m de erro na medição. Uma terra é de 300 metros e outra de 2.000.
Nesse caso, o erro relativo da primeira medição será maior que o do segundo, pois na proporção 1 m representa uma porcentagem maior.
Lot de 300 m:
EP = (1/300) x 100%
Ep = 0,33%
Lote de 2.000 m:
Ep = (1/2.000) x 100%
Ep = 0,05%
2. Medição de alumínio
Em um laboratório, um bloco de alumínio é entregue. Ao medir as dimensões do bloco e calcular sua massa e volume, sua densidade é determinada (2,68 g/cm³).
No entanto, ao verificar a tabela numérica do material, isso indica que a densidade de alumínio é 2,7 g/cm³. Dessa maneira, o erro absoluto e percentual seria calculado da seguinte forma:
EA = 2,7 - 2,68
EA = 0,02 g/cm³.
Ep = (0,02/2,7) x 100%
Ep = 0,74%
3- Participando de um evento
Foi assumido que 1.000.000 pessoas iriam a um determinado evento. No entanto, o número exato de pessoas que foram para este evento foi de 88.000. O erro absoluto e percentual seria o seguinte:
Pode servir a você: variável aleatória: conceito, tipos, exemplosEa = 1.000.000 - 88.000
EA = 912.000
Ep = (912.000/1.000.000) x 100%
Ep = 91,2%
4. Bola cair
O tempo calculado deve levar uma bola para chegar ao solo após ser jogado a uma distância de 4 metros é de 3 segundos.
No entanto, no momento da experimentação, descobre -se que a bola levou 2,1 segundos para chegar ao solo.
EA = 3 - 2.1
EA = 0,9 segundos
Ep = (0,9/2,1) x 100%
EP = 42,8%
5. É preciso um carro para chegar
Estima -se que, se um carro chegar a 60 km, chegará ao seu destino em 1 hora. No entanto, na vida real, o carro levou 1,2 horas para chegar ao seu destino. O erro percentual desse cálculo de tempo seria expresso da seguinte forma:
EA = 1 - 1.2
Ea = -0,2
Ep = (-0,2/1.2) x 100%
EP = -16%
6. Comprimento de medição
Qualquer comprimento é medido por um valor de 30 cm. Verificar a medição desse comprimento é evidente que houve um erro de 0,2 cm. O erro percentual neste caso seria manifestado da seguinte forma:
Ep = (0,2/30) x 100%
Ep = 0,67%
7. Comprimento da ponte
O cálculo do comprimento de uma ponte de acordo com seus aviões é de 100 m. No entanto, ao confirmar esse comprimento, uma vez construído, é evidente que é na verdade 99,8 m de comprimento. O erro percentual seria evidenciado dessa maneira.
EA = 100 - 99,8
Ea = 0,2 m
Ep = (0,2/99,8) x 100
Ep = 0,2%
8. O diâmetro de um parafuso
A cabeça de um parafuso fabricado padrão tem 1 cm de diâmetro.
Pode servir a você: distribuição uniforme contínua: características, exemplos, aplicaçõesNo entanto, ao medir esse diâmetro, observa -se que a cabeça do parafuso realmente tem 0.85 cm. O erro percentual seria o seguinte:
EA = 1 - 0,85
EA = 0,15 cm
Ep = (0,15/0,85) x 100
Ep = 17,64%
9. Peso do objeto
De acordo com seu volume e materiais, estima -se que o peso de um determinado objeto seja de 30 quilos. Uma vez analisado o objeto, observa -se que seu peso real é de 32 quilos.
Nesse caso, o valor do erro percentual é descrito da seguinte forma:
EA = 30 - 32
Ea = -2 quilos
Ep = (2/32) x 100
EP = 6,25%
10. Medição de aço
Em um laboratório, uma folha de aço é estudada. Ao medir as dimensões da folha e calcular sua massa e volume, a densidade do mesmo (3,51 g/cm³) é determinada.
No entanto, ao verificar a tabela numérica do material, isso indica que a densidade do aço é de 2,85 g/cm³. Dessa maneira, o erro absoluto e percentual seria calculado da seguinte forma:
EA = 3,51 - 2,85
Ea = 0,66 g/cm³.
Ep = (0,66/2,85) x 100%
EP = 23,15%
Referências
- Erro percentual. Recuperado de Mathsisfun.com
- Como calcular o erro percentual. Recuperado do pensamento.com

