Valor relativo

Qual é o valor relativo de um número?

Ele valor relativo de um número o Digit de sistema decimal depende da posição que ocupa quando faz parte de uma figura. Portanto, diz -se que é um valor posicional. Um exemplo muito simples: o valor relativo de 1 No número 123, Será 100, Porque eu ocupa a posição das centenas.

Outro exemplo: O número 58 é formado por dígitos 5 e 8. Examinando esse número da direita para a esquerda, o valor relativo de 8 é 8, para estar na posição das unidades e o valor relativo de 5 é 50, para ocupar o local das dezenas. O número é lido "cinquenta -oito".

Por outro lado, os mesmos dígitos têm valores relativos diferentes no número 85, pois trocaram posições. Sempre começando da direita para a esquerda, o valor relativo de 5 neste caso é 5, o valor relativo de 8 é 80 e o número é lido "Oitenta -cinco".

Como encontrar o valor relativo de um número?

O procedimento geral para encontrar o valor relativo de cada dígito é o seguinte:

• O primeiro dígito da direita para a esquerda está na posição das unidades e seu valor é multiplicado por 1.
• O dígito a seguir corresponde às dezenas e é multiplicado por 10.
• A próxima posição corresponde às centenas e o valor do dígito é multiplicado por 100.
• A próxima posição é mil, portanto, o dígito é multiplicado por 1000.

E assim por dia.

Por exemplo, o número 321 pode ser escrito como 3*100 + 2*10 + 1*1, ou equivalente 300 + 20 + 1 1. No exemplo anterior, pode -se ver rapidamente que o valor relativo de 3 é 300, 2 é 20 e 1 é 1.

Pode atendê -lo: propriedade distributiva

Exemplos de valores relativos

Número 727

Para determinar o valor relativo de um dígito, você deve ser guiado pelo seguinte princípio básico da numeração por escrito do sistema decimal:

Qualquer dígito à esquerda de outro representa uma unidade 10 vezes maior e vice -versa: cada dígito à direita de outro, representa uma unidade 10 vezes menor. 

Por exemplo, a figura 727, que diz "setecentos e vinte e sete", consiste em dígitos 2 e 7, com 7 repetidos, mas ocupando posições diferentes.

Lendo 727 da direita para a esquerda, observa -se que o 7 à direita ocupa a posição da unidade; portanto, é multiplicada por 1:

7 x 1 = 7

E seu valor relativo é 7.

O dígito 2 no meio ocupa a posição das dezenas e, para encontrar seu valor relativo, é multiplicado por 10:

2 x 10 = 20

Finalmente no 7 à esquerda extrema tem a posição das centenas. Então você precisa se multiplicar por 100 e seu valor relativo é:

7 x 100 = 700

Observe que somente quando o dígito ocupa a posição da unidade é que seu valor absoluto e seu valor relativo são iguais. Portanto, se o valor relativo do número for VR e seu valor absoluto é VA, a fórmula geral para descobrir que o valor relativo é:

VR = valor absoluto VA × valor de sua posição

Uma figura pode ser escrita como a soma dos valores relativos de seus dígitos, isso é conhecido como notação desenvolvida. Continuando com o exemplo do número 727, você precisa:

727 = 700 + 20 + 7

E se você preferir usar os poderes de 10, o número 727 também é expresso equivalente como:

727 = 7 ∙ 10² + 2 ∙ 10¹ + 7 ∙ 10⁰

Pode atendê -lo: múltiplos de 8: o que são e explicação

Onde os expoentes do poder com base em 10 representam a posição de cada dígito e são chamados Índices. Na figura seguinte, outro exemplo é ilustrado.

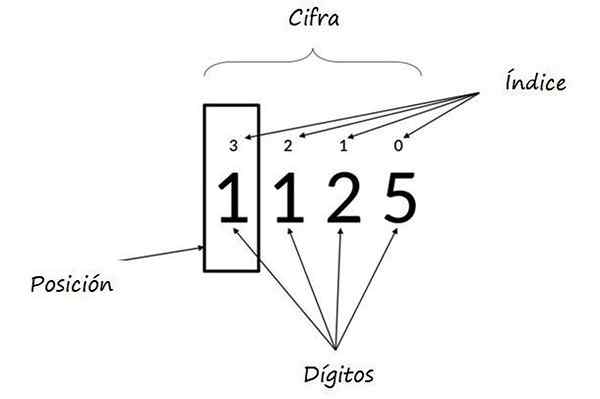No número 1125, o valor relativo de 5 é 5, o 2 é 20, o 1 é 100 e o esquerdo 1 na caixa é 1000. Fonte: Wikimedia Commons.

Número 63

A partir da esquerda para a direita, o 3 está na posição das unidades, portanto:

Valor relativo de 3: 3 x 1 = 3

Quanto a 6, isso está na posição das dezenas, então:

Valor relativo de 6: 6 x 10 = 60

Número 603

Este número é diferente do anterior, porque, embora o valor relativo de 0 seja 0, os outros dígitos têm valores relativos diferentes. Começando da direita para a esquerda como sempre:

• Valor relativo de 3: 3 x 1 = 3
• Valor relativo de 0: 0 x 10 = 0
• Valor relativo de 6: 6 x 100 = 600

Número 630

Nesse caso, 0 está na posição das unidades:

• Valor relativo de 0: 0 x 1 = 0
• Valor relativo de 3: 3 x 10 = 30
• Valor relativo de 6: 6 x 100 = 600

Exercícios resolvidos

Exercício 1

Indique o valor relativo dos números sublinhados:

a) 1209

b) 2782

c) 376

d) 3045

e) 273

Solução

a) O dígito 1 em 1209 ocupa a posição dos mil ou milhares. Portanto, seu valor relativo é 1000.

VR (1) = 1 x 1000 = 1000

b) Os 2 ocupa a posição das unidades em 2782, portanto, seu valor relativo é 2.

c) Em 376, o 7 está na posição das dezenas e:

VR (7) = 7 x 10 = 70.

d) Em 3045, o 4 também está na posição das dezenas:

VR (4) = 4 x 10 = 40.

e) 273 O 3 está no lugar das unidades e seu valor relativo coincide com a figura do dígito, ou seja::

Pode servir você: pirâmide hexagonal

VR (3) = 3 x 1 = 3

Exercício 2

Escreva o número mais baixo de 5 dígitos, sem nenhum é repetido e atenda às seguintes condições:

a) que todos os dígitos são diferentes

b) tem um 7 nos mil

c) o 8 está na posição das unidades.

Solução para

O menor número de 5 dígitos, com todos eles, deve começar por 1, pois, embora 0 seja menor, pois o primeiro dígito à esquerda não conta, portanto, o número procurado é:

10234

Solução b

A posição Millar para 7 corresponde a 7000, mas como você deseja a menor figura possível que contém 5 dígitos, o número deve começar por 1, seguido por 7 e depois 023 nas posições restantes, uma vez que nenhum dígito deve ser repetido.

Portanto, o número é:

17023

Solução c

Conforme solicitado que os 8 estivessem na posição das unidades, deve ser ao extremo direito. Sendo o número menos possível, sem que nenhum de seus 5 dígitos seja repetido, o número procurado é:

10238

Exercício 3

Calcule o valor absoluto e relativo (de cada figura) do número 579.

Solução

Tem que 579 é igual a 5 × 100+7 × 10+9 × 1, ou equivalente, é igual a 500+70+9. Portanto, o valor relativo de 5 é 500, o valor relativo de 7 é 70 e o 9 é 9.

Por outro lado, o valor absoluto de 579 é igual a 579.

Exercício 4

Dê o número 9.648.736, qual é o valor relativo de 9 e primeiro 6 (da esquerda para a direita)? Qual é o valor absoluto do número dado?

Solução

Reescrevendo para o número 9.648.736 é obtido que isso é equivalente a

9 × 1.000.000 + 6 × 100.000 + 4 × 10.000 + 8 × 1.000 + 7 × 100 + 3 × 10 + 6 × 1

ou você pode escrever como

9.000.000 + 600.000 + 40.000 + 8.000 + 700 + 30 + 6.

Para que o valor relativo de 9 seja 9.000.000 e o valor relativo dos primeiros 6 é 600.000.

Por outro lado, o valor absoluto do número fornecido é 9.648.736.