Valor absoluto

Qual é o valor absoluto?

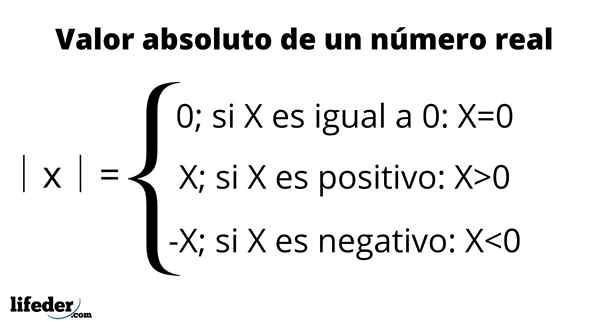
Ele valor absoluto de um número real é definido como a distância entre esse número e 0 da linha real. Por ser uma distância, seu valor é sempre positivo ou zero e igual à figura do número.

O valor absoluto é representado colocando o número entre duas barras verticais, um símbolo lido: "valor absoluto de”, Conforme resumido na tabela a seguir:

Por exemplo, o valor absoluto de -3 é escrito como │ -3│ e é igual a 3. Isso significa que entre -3 e 0 existem três unidades, o que representa os números na linha real. Por outro lado, o valor absoluto de +3 ou simplesmente 3 também é igual a 3, pois medindo sua distância a 0 também são três unidades.

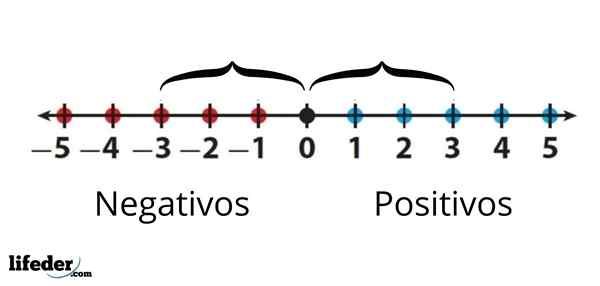O valor absoluto de -3 é igual ao valor absoluto de +3, uma vez que a distância entre um a 0 é a mesma é a mesma

Em resumo, o valor absoluto de um número é a mesma figura do número, mas sempre com um sinal positivo.

Propriedades de valor absoluto

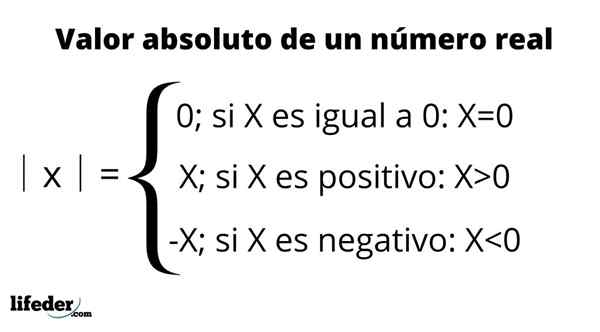Definição de valor absoluto

As principais propriedades do valor absoluto:

• 1) O valor absoluto de um número é sempre positivo ou 0, portanto:

│x│≥ 0

• 2) O valor absoluto de zero também é zero, ou seja, │0│ = 0, portanto, pode -se afirmar que:

│x│ = 0, sim y somente se x = 0

• 3) Para cada número X que pertence ao conjunto de números reais, o valor absoluto de x é igual ao valor absoluto de - x:

│x│ = │ - x│

• 4) Se o valor absoluto de um número x for a, significa que existem duas opções para esse número: i) x = +a ou ii) x = -a.

Pode servir você: Mary Travels 2/4 do Cyclepist, Melissa viaja 4/8 e Anahi viaja 3/6

Por exemplo, se o valor absoluto de um número for 5, as duas possibilidades são de que o número é +5 ou -5.

Operações com valor absoluto

As propriedades a seguir são muito úteis para fazer operações com valores absolutos:

• 5) Para "x" e "y" que são dois números reais, a seguinte desigualdade é sempre cumprida, chamada desigualdade triangular de valor absoluto:

│x│+│y│ │x+y│

Por exemplo, seja:

x = -6

y = 9

O lado esquerdo da desigualdade é:

│-6│ + │9│ = 6 + 9 = 16

E o lado certo é:

│-6+9│ = │3│ = 3

Obviamente 16 é maior ou igual a 3, e esse é sempre o caso quando os números x e e têm sinais diferentes. Se eles tiverem sinais iguais, a igualdade é obtida. Veja este outro exemplo com dois outros valores diferentes:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3≥│-8│

De fato:

8 = 8

• 6) O produto dos respectivos valores absolutos de dois número real "x" e "y" é igual ao valor absoluto do produto dos números:

│x│ ∙ │y│ = │x ∙ y│

Novamente são os valores:

x = -6

y = 9

Então:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Que é igual a:

│ (-6) ∙ 9│ = │-54│ = 54

• 7) O quociente do valor absoluto de dois números reais "X" e "Y", com o denominador diferente de 0, é o valor absoluto do quociente entre esses números:

Desde que e ≠ 0.

Exemplo:

Exemplos de valor absoluto

Exemplos simples

Cálculo do valor absoluto de qualquer número real é muito simples, por exemplo, o valor absoluto dos seguintes números é:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Cálculos com o valor absoluto de um número real

Execute as seguintes operações que envolvem o valor absoluto:

A) 2⋅│8│ + 5⋅│ -16│ -4│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Pode atendê -lo: metade dos 15

Esta é uma operação combinada, por isso é preferível resolvê -la por etapas. O primeiro valor absoluto é:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

O segundo valor absoluto que aparece é calculado da seguinte forma:

│81 ÷ (-3) │ = │-27│ = 27

Em seguida, os resultados obtidos são coletados e o cálculo final é realizado:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19- 6 + 27 = 40

A distância entre dois pontos na linha real

O valor absoluto aparece em muitas aplicações, como encontrar a distância entre dois números que pertencem à linha real. Se A é um número real, está localizado na linha real no ponto cuja abcissa é "a", o mesmo acontece com um número real B.

Deixe "A" e "B" dois números na linha real, a distância que os separa é:

d_Ab = │b - a│

Que também pode ser calculado por:

d_Ab = │a - b│

Por exemplo, a distância entre a = 5 e b = 12 é:

D = │5−12│ = │12−5│ = 7

Dessa maneira, o valor absoluto da subtração entre dois números reais é simplesmente a distância que os separa na linha real.

Função de valor absoluto

A função de valor absoluto é um aplicativo que vai no conjunto de números reais ℛ até ℛ ℛ⁺, que corresponde a cada número real de seu valor absoluto. É definido por:

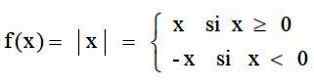
E seu gráfico tem o formulário V típico:

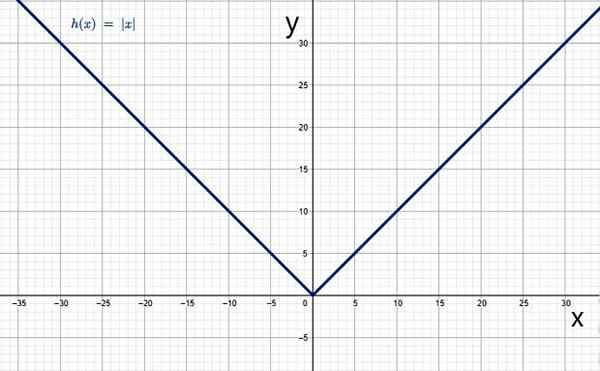O valor absoluto como uma função. Fonte: f. Zapata através da Geogebra.

Características da função de valor absoluto

-Seu domínio é o conjunto de todos os números reais.

-É contínuo.

-É par, já que é cumprido que f (x) = f (-x), portanto o eixo vertical é um eixo de simetria.

-O intervalo da função de valor absoluto é o conjunto de reais positivos, incluindo 0, pois a função sempre representa uma distância, e isso é sempre positivo ou nulo.

Pode atendê -lo: qual é a diretriz? (Geometria)

-É uma função por seções ou peças.

-Diminui no intervalo (-∞, 0) e cresce em (0,+∞).

O argumento do valor absoluto também pode ser uma função quadrática ou outra, por exemplo, pode ser definida:

• f (x) = │x²-5x+3│
• g (x) = │sen x│

O valor absoluto é responsável por se tornar positivo as imagens do argumento que têm um sinal negativo.

Exercícios resolvidos

Exercício 1

Avalie as seguintes expressões algébricas com valor absoluto:

a) │2x -5│ + │ --x + 1│ em x = 3

b) │ (x - 5) ÷ (x+4) │ em x = −1

Solução para

│2⋅3−5│ + │ - 3 + 1│ = │6−5│ + │ - 2│ = │1│ + 2 = 3

Solução b

│ (−1−5) ÷ (−1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Exercício 2

Qual é o conjunto de valores que representam a seguinte desigualdade?

│x│≤ 3

Solução

A desigualdade representa todos os números reais cujo valor absoluto é menor ou igual a 3; portanto, é o conjunto de todos os números entre -3 e +3, incluindo estes.

Na notação do intervalo, permanece:

[-3,3]

Exercício 3

Resolva a seguinte equação com valor absoluto:

│2x-1│ = 5

Solução 

Como indicado anteriormente, para resolver uma equação com valor absoluto, é necessário considerar as duas opções. Quero dizer, sim:

│f (x) │ = c

Então:

1) f (x) = c

2) f (x) = -c

Portanto, esta equação, cujo argumento é linear, tem duas soluções:

Primeira solução

2x - 1 = 5

2x = 6 ⇒ x₁ = 3

Segunda solução

2x - 1 = -5

2x = -4 ⇒ x₂ = -2

Ao avaliar x₁ = 3 ou x₂ = -2 Na equação original, uma igualdade deve ser obtida, dessa maneira é verificado que os valores obtidos são a solução da equação proposta. Em efeito:

│ (2⋅3) -1│ = │6-1│ = 5

E ao tentar com a segunda opção, também é obtida uma igualdade:

│2⋅ (-2) -1│ = │-4-1│ = 5

Referências

1. Baldor, a. 2005. Álgebra. Grupo de pátria cultural.
2. Larson, r. 2012. Pré -cálculo. 8º. Edição. Cengage Learning.
3. Hoffman, J. Seleção de questões de matemática. Volume 2.
4. Stewart, J. 2007. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
5. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.