Hendecágono

O que é um Endecagon?

Ele hendecágono, Tambem chamando UNDECÁGONO, É uma figura geométrica plana com 11 lados que pertencem à família Polgons.

Estes são nomeados de acordo com a quantidade de lados que têm e, no caso do Endecagon, seu nome deriva das palavras gregas "Hendeka" e "Gona": onze e vértice, respectivamente, de acordo com o fato de que o Endecagon tem 11 vértices ou dicas.

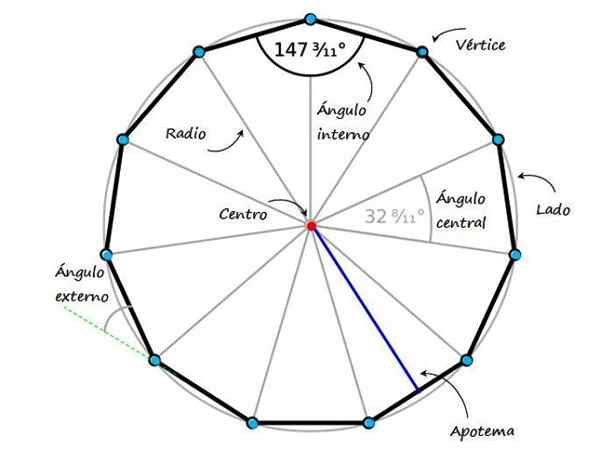
figura 1. Um EndeCagon regular e seus elementos. Fonte: f. Sapato modificado da Wikimedia Commons.

Os polígonos regulares compartilham uma série de características distintas, particular. A Figura 1 mostra um Endecagon regular e suas propriedades mais significativas:

• Lados, Um total de 11.
• Vértices, Há também 11 pontos que se juntam a dois lados consecutivos (na figura anterior estão os pontos azuis e na Figura 3 eles também são nomeados com letras maiúsculas).
• Centro, ponto equidistante de ambos os vértices e lados.
• Diagonais, Linhas que se juntam a um vértice com outro vértice não consecutivo, no total de 44.
• Ângulos internos, Aqueles que são formados entre dois lados adjacentes no lado interno do Endecagon. Se o EndeCagon for regular, todos os ângulos internos medem 147 ^3/11 º.
• Ângulos externos, Eles são formados entre um lado e o prolongamento de um dos lados consecutivos.
• Rádio, Distância do centro para um vértice.
• Ângulo central, que no caso de Endecagon regular mede 32 ^11/11 º, cujos lados são dois segmentos adjacentes e o vértice do ângulo coincide com o centro.
• Apótema, segmento perpendicular que se junta ao centro de um lado com o centro da figura.

Pode atendê -lo: Hipparco de Nicea: Biografia e Contribuições para a Ciência

Como fazer um endecagon regular?

Para desenhar um EndeCagon regular, cujos lados medem o mesmo, você precisa de regra e bússola. Uma maneira de fazer o layout é seguir estas etapas:

1.- Desenhe uma circunferência e dois diâmetros, um vertical e outro horizontal. Os pontos da circunferência determinados por esses diâmetros são nomeados e B (diâmetro horizontal) e C e D (diâmetro vertical).

2.- Abra a bússola com a medida do raio do círculo, apoie a ponta no ponto D do diâmetro do CD e desenhe um primeiro arco que cruze a circunferência no ponto e.

3.- Com essa mesma medida, apoie a ponta da bússola no ponto A e desenhe um segundo arco que cruze a circunferência no ponto F e, ao mesmo tempo, passa pelo centro do mesmo.

4.- Abra a batida com a ponta suportada por E e para o ponto F, desenhando um terceiro arco que corta o diâmetro vertical no ponto G.

5.- Agora, abra a bússola entre os pontos F e G. Esta será a medida do lado Endecagon. A ponta da bússola é apoiada em F e desenha um quarto arco que corta a circunferência no ponto H, o lado FH já pertence ao Endecagon e é desenhado juntando -se aos pontos com a ajuda da regra.

6.- A ponta da bússola repousa sucessivamente no ponto H e é elaborada com cuidado, juntando -se aos pontos que são determinados por segmentos, até os onze lados do polígono.

Exemplos de Endecágonos

Existem vários tipos de EndeCargons, de acordo com a medida de seus lados e os de seus ângulos internos, abaixo de alguns exemplos:

Endeconistas regulares e irregulares

-Regular, Se todos os lados e ângulos internos medirem o mesmo.

Pode atendê -lo: Número ou Número e Número E: quanto ok, propriedades, aplicações

-Irregular, Quando seus lados têm medida diferente.

A figura a seguir mostra um endecagon regular no contorno interno de um dólar americano com a figura de Susan B. Anthony (1820-1906), ativista dos direitos das mulheres nascidos em Massachusetts, Estados Unidos. O Endecagon também foi usado como parte do design de outras moedas em todo o mundo.

Figura 2. Um Endecagon regular que faz parte do projeto Dollar Susan B. Anthony, cunhado entre 1979 e 1981, e posteriormente lançado novamente em 1999. Fonte: Wikimedia Commons.

EndeCargons convexos e côncavos

Os enecargons diferem de acordo com seus ângulos internos, por exemplo, eles podem ser:

-Convexo, Se os ângulos internos forem menores de 180º.

-Côncavo, Quando há ângulos internos maiores que 180º.

O EndeCagon que decora o dólar Susan B. Anthony é convexo, uma vez que a medida de qualquer um de seus ângulos internos é menor que 180º. Seu valor é calculado através de uma fórmula que depende do número de lados da figura (consulte a seção a seguir).

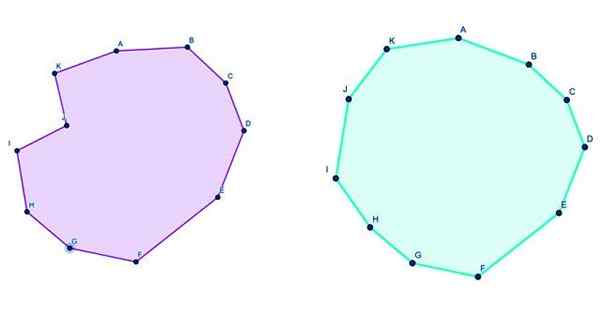Figura 3. À esquerda um enecagon convexo e à direita um endecagon côncavo. Fonte: f. Zapata através da Geogebra.

Fórmulas para o Endecagon

Fórmula para ângulos internos

Para determinar a medida i em graus, dos ângulos internos de qualquer polígono regular de n lados, a seguinte fórmula é usada:

 Substituindo o número de lados do endecagon n = 11 na fórmula é obtido:

 E como os ângulos internos do EndeCagon regular são menores de 180º, esse número é um polígono convexo.

A soma dos ângulos internos de um polígono regular é encontrada por esta fórmula, válida para todo e maior que 2:

Pode servir a você: ângulos na circunferência: tipos, propriedades, exercícios resolvidos

S = (n - 2) x 180º

Substituindo n = 11 resultados:

S = (11 - 2) x 180º = 1620º

Ângulos externos

Para conhecer a medida dos ângulos internos, é aplicado que a soma de um ângulo interno e externo seja igual a 180º:

180 º - 147 ^3/11º = 32 ^11/11º.

Perímetro

O perímetro é a soma dos lados do Endecagon, regular ou não. No caso de Endecagon regular, se ℓ É o comprimento de um lado, o perímetro está se multiplicando por n, A quantidade de lados.

Portanto, o perímetro P do EndeCagon regular é:

P = 11 ℓ

Área

Conhecendo o lado, a área pode ser calculada com a fórmula:

Que é aproximadamente:

A = 9.3656 ∙ ℓ²

Outra maneira de encontrar a área, desde que o Endecagon seja regular, é dividi -la em triângulos base iguais ao lado ℓ e altura igual ao comprimento do apothem l l l_PARA.

A área de cada triângulo é calculada por:

Área = base x altura /2

Que, dependendo do apothem, também é escrito como:

Área = ℓ. eu_PARA /2

E a área total do Endecagon está multiplicando a área do triângulo até 11:

A = 11ℓ. eu_PARA /2

Em termos de perímetro, a área regular de Endecagon é:

A = p. eu_PARA /2

Diagonais

O número de diagonais é calculado fazendo n = 11 na fórmula a seguir:

 D = [11 x (11-3)]/2 = 44 diagonais.

Exercício resolvido

Calcule o perímetro e a área de um endecágono regular de 20 cm do lado.

Solução

O perímetro é:

P = 11 ℓ =11 × 20 cm = 220 cm.

E sua área é:

A = 9.3656 ∙ ℓ²= 9.3656 × (20 cm)²= 3746.2 cm²

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Professor de desenho. Endecágono inscrito em uma circunferência (11 lados polígono). Recuperado de: youtube.com.
3. Problemas e equações. Calculadora de área e perímetro do Endecagon regular. Recuperado de: Problemas Syuses.com.
4. Sangaku Maths. Elementos de um polígono e sua classificação. Recuperado de: sangakoo.com.
5. Resolução automática de problemas de geometria. O Endecagon. Recuperado de: scuolatrica.Item.
6. Wolfram Mathworld. Hendecágono. Recuperado de: Mathworld.Volfrâmio.com.