Trinomial quadrado perfeito

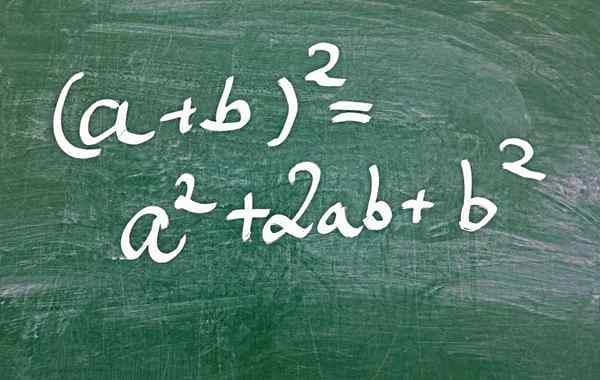figura 1.- Uma das maneiras de obter um trinômio quadrado perfeito é através do quadrado da soma

Qual é o trinômio quadrado perfeito?

O trinômio quadrado perfeito é que o polinômio de três termos, dois dos quais são quadrados perfeitos das quantidades A e B e são precedidos pelo mesmo sinal, enquanto o terceiro termo é exatamente o duplo produto de A e B, sendo capaz de ser de um sinal diferente.

Um trinômio quadrado perfeito é obtido pelo quadrado a soma ou diferença de um binomial e algebricamente, sua forma é a seguinte:

para² ± 2 ∙ ab + b²

Como pode ser visto, o trinomial quadrado perfeito contém:

• Dois termos quadráticos não semelhantes precedidos pelo mesmo sinal: a² e B²
• Um terceiro termo 2 ∙ ab, que é o produto duplo das raízes quadradas dos termos quadráticos e que podem ser precedidos por um sinal positivo ou negativo.

Trinômios quadrados perfeitos podem ser uma ou mais variáveis. Por exemplo, o seguinte trinomial é um quadrado perfeito de uma variável:

• x² + 6x + 9

Observe que os primeiros termos (x²) e o terceiro (9) são quadrados, respectivamente, das quantidades chamadas A e B. De fato, x² É o quadrado de x e 9 é o quadrado de 3. Dessa forma, você pode escrever o seguinte:

a = x

B = 3

E o termo restante é o produto duplo de x e 3:

6x = 2 ∙ 3 ​​∙ x

Uma vez que a verificação é feita, é certo que esse trinomial é um quadrado perfeito.

Exemplos

Figura 2.- Exemplos de trinômios quadrados perfeitos. Fonte: f. Zapata.

Os trinômios quadrados perfeitos também aparecem em duas ou mais variáveis, por exemplo:

4x² + 4xy + e²

É um trinômio em duas variáveis: "x" e "y". Pode -se ter certeza de que é um trinômio quadrado perfeito, pois apresenta dois termos quadráticos:

4x² = (2x)²

e² = (y)²

E o termo restante é o produto duplo das respectivas raízes quadradas: "2x" e "y":

Pode servir a você: Orthoedro: fórmulas, área, volume, diagonal, exemplos

4xy = 2 ∙ 2x ∙ e

Os trinômios apresentados até agora são o grau 2 na variável "x", mas eles não precisam necessariamente ser assim. O seguinte trinomial é o grau 4 em "X":

9x⁴ - 30x²Yz + 25y²z²

É facilmente verificado que este é um trinômio quadrado perfeito. O primeiro termo é o quadrado 3x perfeito², Desde (3x²)² = 9x⁴.

O termo 25y²z² é igual a (5yz)². Finalmente, o termo restante é 2 ∙ 3x²∙ 5yz = 30 x²e z.

Por outro lado, os trinômios mostrados abaixo não são trinômios quadrados perfeitos:

• x²  + 8x - 16

Não é um trinômio quadrado perfeito porque 16, embora seja 4², É precedido por um sinal negativo, enquanto o outro termo quadrático (x²) é positivo.

• x²  - 15x + 25

Nem é um trinômio quadrado perfeito, porque, embora tenha dois termos quadráticos: x² e 5², O termo 15x não é igual a 2 ∙ 5 ∙ x x.

• 4x²  + 10x + 32

Este trinomial não é quadrado perfeito, pois contém apenas um termo quadrático: 4x² = (2x)².

Quadrado de uma soma e quadrado de uma diferença

Trinômios quadrados perfeitos são obtidos desenvolvendo dois tipos de produtos notáveis:

• O quadrado da soma.
• O quadrado da diferença.

Primeiro, o desenvolvimento é obtido a partir da propriedade distributiva, pois levantar o binomial quadrado significa multiplicando -a por si mesma:

(A ± b)² = (a ± b) × (a ± b) = a² ± a ∙ b ± b ∙ a + b² = a² ± 2a ∙ b + b²

O trinômio obtido é um resultado que é memorizado com apenas um pouco de prática e é um tipo de atalho que facilita o desenvolvimento, e é por isso que é chamado de produto notável.

Pode atendê -lo: números transcendentes: o que são, fórmulas, exemplos, exercícios

Os seguintes trinômios são facilmente obtidos por produto notável, sem a propriedade distributiva que aplica.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 e² +20xy + 4x²

Fatoração de um trinômio quadrado perfeito

Uma operação frequente e necessária na álgebra é a fatorização do trinômio quadrado perfeito, através do qual o trinômio é expresso como o quadrado de uma soma ou subtração de dois termos (um binomial).

É a operação reversa desenvolver o produto notável, pois ter o trinomial resultante, a idéia é obter o binomial que dá origem a ele quando se eleva ao 2.

Por exemplo, no trinômio quadrado perfeito 4x analisado anteriormente² + 4xy + e², O que é o binomial que, quando é quadrado, dá origem a você?

As respectivas raízes quadradas dos termos quadráticos são:

√ (4x²) = 2x

Que é equivalente a: 4x² = (2x)²

√ (e²) = y

Equivalente a dizer isso: e² = (y)²

Portanto:

4x² + 4xy + e² = (2x + y)²

E qual é o binomial que origina o trinomial quadrado perfeito 9x⁴ - 30x²Yz + 25y²z²? Novamente, as raízes quadradas dos termos quadráticos são extraídos:

√ (9x⁴) = 3x²

√ (25 e²z²) = 5yz

Então:

(3x² - 5yz)² = 9x⁴ - 30x²Yz + 25y²z²

Exercícios resolvidos

Exercício 1

Em cada um dos seguintes trinômios, complete o espaço em branco com o termo que está faltando para ser um trinômio quadrado perfeito:

sou² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Solução para

De acordo com a fórmula do produto notável:

Pode servir a você: ângulos complementares: qual e como eles são calculados, exemplos, exercícios

(A ± b)² = A² ± 2a ∙ b + b²

Do trinomial:

m² + 18m + _____

Segue que:

a = m (para que² = m²)

Além disso, o termo central é: 2 ∙ a ∙ b = 2m ∙ b = 18m, portanto b = 9 e seu quadrado é 9² = 81. Cara, pela fórmula do produto notável, o trinomial é assim:

(M + 9)² = M² + 18m + 81

• Solução b

Neste trinomial:

4x² - _____ + 64

Você pode saber e B:

A = √ (4x²) = 2x

B = √64 = 8

Portanto, o termo ausente é o produto duplo de A e B:

2 ∙ ab = 2 ∙ 8 ∙ 2x = 32x

E o trinomial procurado é:

4x² - 32x + 64

• Solução c

No trinomial:

_____ + 30n + 25

O primeiro termo está faltando, mas sabe -se que:

B = √25 = 5

E

2 ∙ ab = 2 ∙ a ∙ 5 = 10a = 30n

Portanto, a = 3n e o trinomial procurado é:

9n² + 30n + 25

Exercício 2

Verifique se o próximo é um trinômio quadrado perfeito e fatorá -lo:

16y² - 24yz + 9z²

• Solução

Primeiro, está provado que os termos quadráticos são precedidos pelo mesmo sinal e, em seguida, as respectivas raízes quadradas são encontradas:

A = √ (16y²) = 4y

B = √ (9z²) = 3z

Então você deve verificar se o termo restante é o produto duplo de A e B:

2 ∙ ab = 2 ∙ 4y ∙ 3z = 24yz

Se for, o trinomial pode ser fator que o quadrado de uma diferença, uma vez que o termo central é precedido por um sinal negativo:

16y² - 24yz + 9z² = (4y - 3z)²

Referências

1. Jiménez, r. 2008. Álgebra. Prentice Hall.
2. Aulas de matemática de Kate. Trinômios quadrados perfeitos. Recuperado de: Katesmathlensons.com.
3. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
4. Zill, d. 2008. Preccultment com avanços de cálculo. 4º. Edição. McGraw Hill.