Propriedades do trapézio retângulo, relacionamentos e fórmulas, exemplos

A trapézio retângulo É uma figura plana de quatro lados, de modo que dois deles são paralelos entre si, chamados bases E também um dos outros lados é perpendicular às bases.

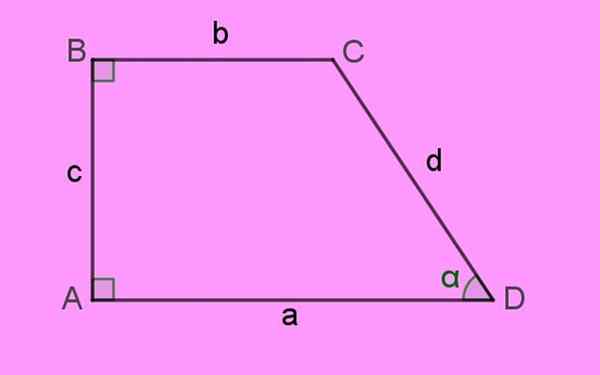
Por esse motivo, dois dos ângulos internos são retos, ou seja, eles medem 90º. Daí o nome de "retângulo" que é dado à figura. A imagem a seguir de um trapézio retângulo esclarece estas características:

[TOC]

Elementos do trapézio

Os elementos do trapézio são:

-Bases

-Vértices

-Altura

-Ângulos internos

-Base média

-Diagonais

Detalhamos esses elementos com a ajuda das Figuras 1 e 2:

figura 1. Um trapézio retângulo, caracterizado por ter dois ângulos internos de 90º: a e b. Fonte: f. Zapata.

As laterais do trapézio retângulo são indicadas pelas letras minúsculas A, B, C e D. Os cantos da figura ou Vértices Eles são indicados em letras maiúsculas. Finalmente Ângulos internos Eles são expressos com cartas gregas.

De acordo com a definição, o bases Deste trapézio são os lados A e B, que, como observados, são paralelos e também têm comprimento diferente.

O lado perpendicular para ambas as bases é o lado c à esquerda, que é o altura h do trapézio. E finalmente há o lado d, que forma o ângulo agudo α com o lado a.

A soma de Ângulos internos de um quadrilateral é 360º. É facilmente apreciado que o ângulo que faltava na figura seja 180 - α.

O base média É o segmento que se junta às feiras médias de lados não paralelos (segmento de EF na Figura 2).

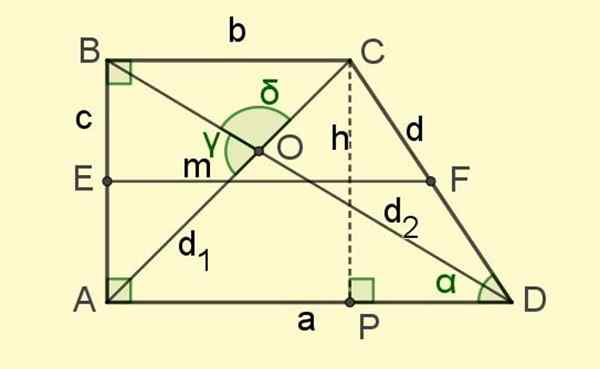Figura 2. Os elementos do trapézio retângulo. Fonte: f. Zapata.

E finalmente há os diagonais D₁ e d₂, os segmentos que unem os vértices opostos e que se cruzam no ponto O (veja a Figura 2).

Relacionamentos e fórmulas

Altura h do trapézio

H = c

Perímetro p

É a medida do contorno e é calculada adicionando os lados:

Perímetro = a + b + c + d

O lado d É expresso em termos de altura ou lado c Através do teorema de Pitágoras:

D = √ (a-b)² + c²

Substituindo no perímetro:

P = a + b + c + √ (a-b)² + c²

Base média

São os corpos semi -Bases:

Base média = (a+b)/2

Às vezes, a base média expressa dessa maneira é encontrada:

Base média = (base principal + base menor) /2

Área

Área A do trapézio é o produto da base média por altura:

A = (Base principal + base menor) x altura /2

A = (a+b) c/2

Diagonais, laterais e ângulos

Vários triângulos aparecem na Figura 2, retângulos e não -rectangles. Para aqueles que são triângulos certos, eles podem ser aplicados pelo teorema de Pitágoras e aqueles que não o fazem, os teoremas do cosseno e da mama.

Pode atendê -lo: números transcendentes: o que são, fórmulas, exemplos, exercícios

Dessa maneira, existem relações entre os lados e entre os lados e os ângulos internos do trapezio.

Triângulo CPA

É retângulo, suas pernas são iguais e valem B, enquanto a hipotenusa é a diagonal D₁, portanto:

d₁² = b² + b² = 2b²

Triângulo Dab

Também é retângulo, as pernas são para e c (ou também para e h) E a hipotenusa é D₂, de maneira que:

d₂² = a² + c² = a² + h²

Triângulo da CDA

Como este triângulo não é retângulo, o teorema de cosseno é aplicado ou também a mama.

De acordo com o teorema do Coseno:

d₁² = a² + d² - 2AD cos α

Triângulo CDP

Este triângulo é retângulo e, com seus lados, são construídas as razões trigonométricas do ângulo α:

sin α = h/d

cos α = PD/D

Mas o lado Pd = A - B, portanto:

cos α = (a -b) / d → a - b = d cos α

a = b + d cos α

Você também tem:

Tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)

Triângulo CDB

Neste triângulo, temos o ângulo cujo vértice está em c. Não está marcado na figura, mas no começo se destacou que vale 180 - α. Este triângulo não é retângulo, portanto o teorema de cosseno ou o teorema da mama pode ser aplicado.

Agora, pode -se demonstrar facilmente que:

Sen (180 - α) = sin α

cos (180 - α) = - cos α

Aplicando o teorema do Coseno:

d₂² = d² + b² - 2db cos (180 - α) = D² + b² + 2dB cos α

Exemplos de retângulos

Os trapézios e, em particular, os retângulos são encontrados em muitos lados, e às vezes nem sempre. Aqui temos vários exemplos:

TRAPECIO como um elemento de design

Figuras geométricas abundam na arquitetura de numerosos edifícios, como esta igreja em Nova York, que mostra uma estrutura na forma de trapezoidal retângulo.

Além disso, a forma trapezoidal é frequente no design de recipientes, recipientes, lâminas (Cortador ou exato), folhas e design gráfico.

Figura 3. Anjo dentro de um trapézio retângulo em uma igreja em Nova York. Fonte: David Goehring através do Flickr.

Gerador de ondas trapezoidal

Os sinais elétricos podem não apenas ser quadrados, sinos ou triangulares. Existem também sinais trapezoidais que são úteis em vários circuitos. Na Figura 4, há um sinal trapezoidal composto por dois retângulos. Entre eles, eles formam um único trapézóide isósceles.

Pode atendê -lo: divisores de 8: o que são e uma explicação fácil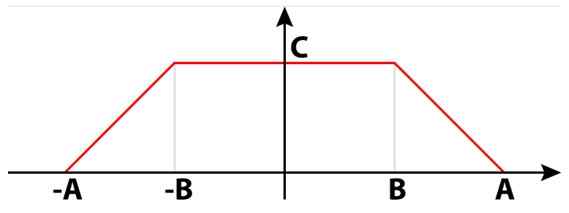Figura 4. Um sinal trapezoidal. Fonte: Wikimedia Commons.

No cálculo numérico

Para calcular numericamente a integral definida da função f (x) entre A e B, a regra do trapézio é usada para aproximar a área sob o gráfico de f (x). Na figura a seguir, à esquerda, as se aproximam de um único trapézóide retângulo.

Uma abordagem melhor é a da figura certa, com vários retângulos.

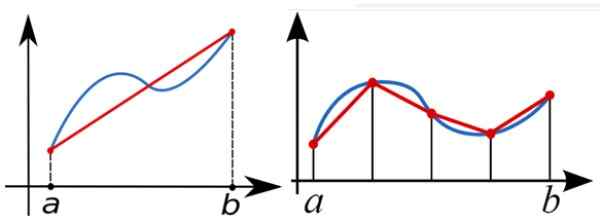Figura 5. Uma integral definida entre A e B nada além da área sob curva f (x) entre esses valores. Um trapézio retângulo pode servir como a primeira abordagem dessa área, mas quanto mais trapezoides forem usados, melhor a abordagem. Fonte: Wikimedia Commons.

Feixe de carga trapezoidal

As forças nem sempre estão concentradas em um único ponto, uma vez que os corpos em que eles agem têm dimensões apreciáveis. É o caso de uma ponte através da qual os veículos circulavam continuamente, a água de uma piscina nas paredes verticais do mesmo ou um teto em que água ou neve se acumula.

É por isso que as forças são distribuídas por unidade de comprimento, superfície ou volume, dependendo do corpo em que agem.

No caso de um feixe, uma força distribuída por unidade de comprimento pode ter várias distribuições, por exemplo, a do trapézio retângulo mostrado abaixo:

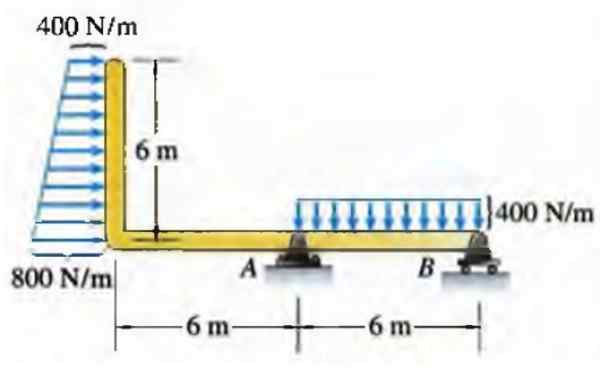Figura 6. Carrega em um feixe. Fonte: Bedford, para. mil novecentos e noventa e seis. Estático. Addison Wesley Inter -American.

Na realidade, nem sempre as distribuições correspondem a formas geométricas regulares como essa, mas podem ser uma boa abordagem em muitos casos.

Como ferramenta educacional e de aprendizado

Blocos e folhas com formas geométricas, incluindo trapezoides, são muito úteis para as crianças se familiarizarem desde tenra idade com o mundo fascinante da geometria.

Figura 7. Blocos com formas geométricas simples. Quantos retângulos estão escondidos nos blocos? Fonte: Wikimedia Commons.

Exercícios resolvidos

- Exercício 1

No trapézio retângulo da Figura 1, a maior base vale 50 cm e a menor base é igual a 30 cm, também é conhecido que o lado oblíquo mede 35 cm. Encontrar:

a) ângulo α

b) Altura

c) perímetro

d) base média

e) área

f) Diagonal

Solução para

Os dados da instrução estão resumidos desta maneira:

A = base superior = 50 cm

B = Base menor = 30 cm

D = lado inclinado = 35 cm

Pode atendê -lo: operações básicas

Para encontrar o ângulo α, visitamos a seção Fórmulas e Equações, para ver qual é melhor se adequar aos dados oferecidos. O ângulo procurado é encontrado em vários dos triângulos analisados, por exemplo, o CDP.

Lá temos essa fórmula, que contém os dados desconhecidos e também os dados que conhecemos:

cos α = (a-b) / d

Portanto:

α = arcos [(a-b) / d] = arcos [(50-30) / 35] = arcos 20/35 = 55.15 º

Solução b

Da equação:

sin α = h/d

H:

h = d.sin α = 35 sen 55.15 º cm = 28.72 cm

Solução c

O perímetro é a soma dos lados e, como a altura é igual ao lado C, temos que::

C = h = 28.72 cm

Portanto:

P = (50 + 30 + 35 + 28.72) cm = 143.72 cm

Solução d

A base média são os corpos semi -Bases:

Base média = (50 + 30 cm)/2 = 40 cm

Solução e

A área do trapezóide é:

A = base média x altura = 40 cm x 28.72 = 1148.8 cm².

Solução f

Para a diagonal d₁ Esta fórmula pode ser usada:

d₁² = b² + b² = 2b²

d₁²= 2 x (30 cm)² = 1800 cm²

d₁ = √1800 cm² = 42.42 cm

E para a diagonal d₂:

d₂² = d² + b² + 2dB cos α = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² Cos 55.15 º = 3325 cm²

d₂ = √ 3325 cm² = 57.66 cm

Esta não é a única maneira de encontrar D₂, já que há também o triângulo DAB.

- Exercício 2

O gráfico de velocidade a seguir, dependendo de um celular que possui um movimento retilíneo uniformemente acelerado. Calcule a distância percorrida pelo celular durante o intervalo de tempo entre 0.5 e 1.2 segundos.

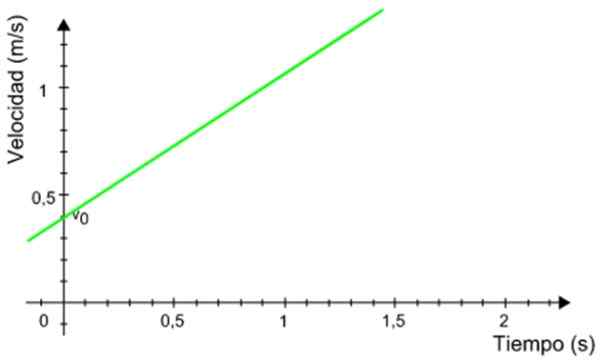Figura 8. Gráfico contra o tempo de um celular com o movimento de renoto de uniformalmente acelerado. Fonte: Wikimedia Commons.

Solução

A distância percorrida pelo celular é equivalente à área sob o gráfico, delimitada pelo intervalo de tempo indicado.

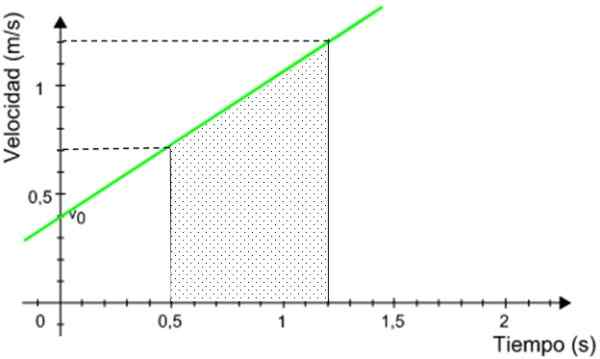Figura 9. A distância percorrida pelo celular é equivalente à área sob os gráficos. Fonte: modificado por f. Zapata.

A área sombreada é a área de um trapézio retângulo, dado por:

A = (Base principal + base menor) x altura /2

A = (1.2 + 0.7) m/s x (1.vinte.5) s/2 = 0.665 m

Referências

1. Baldor, a. 2004. Geometria plana e espacial com trigonometria. Publicações culturais.
2. Bedford, a. mil novecentos e noventa e seis. Estático. Addison Wesley Inter -American.
3. Jr. Geometria. 2014. Polígonos. Lulu Press, Inc.
4. Onlinemschool. Trapézio retângulo. Recuperado de: é.Onlinemschool.com.
5. Resolução automática de problemas de geometria. O trapézio. Recuperado de: scuolatrica.Item
6. Wikipedia. TRAPECIO (GEOMETRIA). Recuperado de: é.Wikipedia.org.