Teorema fundamental da demonstração aritmética, aplicações, exercícios

Ele O teorema fundamental da aritmética Ele afirma que qualquer número natural maior que 1 pode ser quebrado como um produto de números primos - segurando um pouco - e esse formulário é único para esse número, embora a ordem dos fatores possa ser diferente.

Lembre -se de que um número primo p É o que só admite como divisores positivos e 1. Os seguintes números são primos: 2, 3, 5, 7, 11, 13 e assim por diante, já que existem infinitos. O número 1 não é considerado primo, por ter um único divisor.

figura 1. Euclides (à esquerda) demonstrou o teorema fundamental da aritmética em seus elementos de livro (350 a.C.), E a primeira demonstração completa é devido a Carl F. Gauss (1777-1855) (direita). Fonte: Wikimedia Commons.

Por sua parte, os números que não atendem aos acima são chamados números compostos, Como 4, 6, 8, 9, 10, 12, 14 ... vamos pegar o número 10, por exemplo, e imediatamente vemos que ele pode ser quebrado como um produto de 2 e 5:

10 = 2 × 5

2 e 5 são, de fato, números primos. O teorema afirma que isso é possível para qualquer número n:

Onde p₁, p₂, p₃… P_r Eles são números primos e k₁, k₂, k₃,... k_r São números naturais. Para que os números primos agem como tijolos a partir dos quais, por multiplicação, números naturais são construídos.

[TOC]

Demonstração do teorema fundamental da aritmética

Começa a demonstrar que cada número pode se decompor em fatores primos. Ser um número natural n> 1, primo ou composto.

Por exemplo, se n = 2, pode ser expresso como: 2 = 1 × 2, que é primo. Da mesma maneira, prosseguimos com os seguintes números:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Continuamos assim, decompondo todos os números naturais até atingirmos o número n -1. Vamos ver se podemos fazer isso com o número a seguir: n.

Se n é primo, podemos decompô -lo como n = 1 × n, mas suponha que N seja composto e tenha um divisor D, logicamente menor que n:

Pode servir a você: Estatística descritiva: história, características, exemplos, conceitos

1< d < n.

Sim n/d = p₁, com p₁ Um número primo, então n é escrito como:

n = p₁.d

Se D é primo, não há mais nada a fazer, mas se não for, existe um número n₂ que é um divisor de D e menor que isso: n₂ < d, por lo que d podrá escribirse como el producto de n₂ Para outro primo Número P₂:

d = p₂ n₂

Que substituindo o número original n daria:

n = p₁ .p₂ .n₂

Agora suponha n₂ Nem é um número primo e nós o escrevemos como o produto de um número primo p₃, Para um divisor de seu₃, tais que n₃ < n₂ < n₁ < n:

n₂ = p₃.n₃ → n = P₁ p₂ p₃.n₃

 Repitamos este procedimento um número finito de vezes até você obter:

n = p₁.p₂.p₃ … P_r

Isso significa que é possível decompor todos os números inteiros de 2 para o número n, como um produto de números primos.

Singularidade de decomposição em fatores primos

Vamos verificar agora que, exceto pela ordem dos fatores, essa decomposição é única. Suponha que você possa escrever de duas maneiras:

n = p₁.p₂.p₃ … P_r = q_1.q₂.q₃… Q_s  (com r ≤ s)

Claro q₁, q₂, q₃… Eles são números primos também. Como p₁ Divida para (Q_1.q₂.q₃… Q_s) Então p₁ É igual a qualquer um dos "q", não importa O que, assim, podemos dizer que P₁ = q₁. Nós dividimos n entre p₁ E nós conseguimos:

p₂.p₃ … P_r =_.q₂.q₃… Q_s

Repetimos o procedimento para dividir tudo entre P_r, Então temos:

1 = q_R+1… Q_s

Mas não é possível chegar a q_R+1… Q_s = 1 quando r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Formulários

Como já dissemos antes, os números primos representam se você quiser, os átomos dos números, seus componentes básicos. Portanto, o teorema fundamental da aritmética tem inúmeras aplicações, as mais óbvias: podemos trabalhar mais facilmente com grandes números se os expressarmos como o produto de números menores.

Pode atendê -lo: números inteiros

Da mesma maneira, podemos encontrar o múltiplo comum máximo (M.c.m.) e o divisor comum máximo (M.C.D.), Um procedimento que nos ajuda a fazer somas de frações com mais facilidade, encontrar raízes de grandes números ou operar com radicais, racionalizar e resolver problemas de aplicação de uma natureza muito diversa.

Além disso, os números primos são extremamente enigmáticos. Um padrão ainda não é reconhecido neles e não é possível saber qual será o seguinte. O maior até os tempos foi encontrado por computadores e tem 24.862.048 dígitos, Embora os novos números primos apareçam com menos frequência todas as vezes.

Números primos na natureza

As cigarras, Cycaked ou Chicharras que vivem no nordeste dos Estados Unidos emergem em 13 ou 17 anos de ciclos. Ambos são números primos.

Dessa forma, Chicharras evita coincidir com predadores ou concorrentes que têm outros períodos de nascimento, nem as várias variedades de Chicharra competem entre si, pois não coincidem durante o mesmo ano.

Figura 2. A Cicada del Este dos Estados Unidos emerge a cada 13 ou 17 anos. Fonte: Pxfuel.

Números primos e compras online

Os números primos são usados ​​em criptografia para manter os detalhes dos cartões de crédito quando você compra compras on -line. Dessa forma, os dados que o comprador chega precisamente para a loja sem se perder ou cair em pessoas sem escrúpulos.

Como? Os dados do cartão são codificados em um número n que pode ser expresso como o produto de números primos. Esses números primos são a chave que revelam os dados, mas são desconhecidos para o público, eles só podem ser decodificados na web para a qual são direcionados.

A decomposição de um número em fatores é uma tarefa fácil se os números forem pequenos (vendo os exercícios resolvidos), mas, neste caso enorme trabalho.

Pode atendê -lo: estimativa pontual

Exercícios resolvidos

- Exercício 1

Decompor 1029 em fatores primos.

Solução

1029 é divisível por 3. Sabe -se porque, ao adicionar seus dígitos, a soma é um múltiplo de 3: 1+0+2+9 = 12. Como a ordem dos fatores não altera o produto, podemos começar por aí:

1029 3

343

1029 = 3 × 343

Por outro lado, 343 = 7³, então:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

E como 3 e 7 são números primos, esta é a decomposição de 1029.

- Exercício 2

Fator trinomial x² + 42x + 432.

Solução

O trinomial é reescrito na forma (x+a). (x+b) e precisamos encontrar os valores de A e B, para que:

A+b = 42; para.B = 432

O número 432 se decompõe em fatores primos e a partir daí é escolhido, por Tanteo, a combinação apropriada para os fatos adicionados a 42.

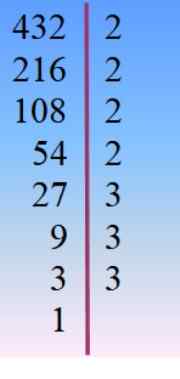
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 =…

A partir daqui, existem várias possibilidades para escrever 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

E todos podem ser encontrados combinando produtos entre fatores primos, mas para resolver o exercício proposto, a única combinação adequada é: 432 = 24 × 18 desde 24 + 18 = 42, então:

x² + 42x + 432 = (x + 24). (x +18)

Referências

1. Baldor, a. 1986. Aritmética teórica prática. Editor Companhia Cultural de Textos Americanos S.PARA.
2. BBC World. O código oculto da natureza. Recuperado de: BBC.com.
3. De Leon, Manuel.Números primos: Guardiões da Internet. Recuperado de: blogs.20 minutos.é.
4. Unam. Teoria do número I: Teorema Fundamental da Aritmética. Recuperado de: TeoriAdenumeros.Wikidot.com.
5. Wikipedia. O teorema fundamental da aritmética. Recuperado de: é.Wikipedia.org.