Definição hiperbólica parabolóide, propriedades e exemplos

A parabolóide hiperbólico É uma superfície cuja equação geral nas coordenadas cartesianas (x, y, z) atende à seguinte equação:

(para)² - (e B)² - Z = 0.

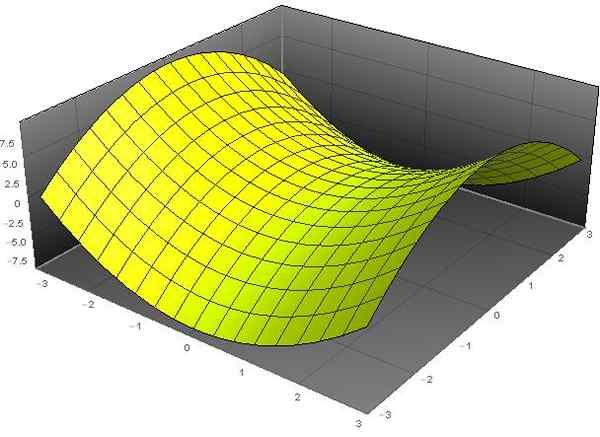
A denominação "parabolóide" vem do fato de que a variável z depende dos quadrados das variáveis ​​x e y. Embora o adjetivo "hiperbólico" seja devido ao fato de a equação de uma hipérbole ter valores fixos de z. A forma dessa superfície é semelhante à de uma cadeira de cavalgada.

figura 1. Parabolóide hiperbólico z = x² - e². Fonte: f. Zapata através de Wolfram Mathematica.

[TOC]

Descrição do parabolóide hiperbólico

Para entender a natureza do parabolóide hiperbólico, será feita a seguinte análise:

1.- O caso específico será tomado a = 1, b = 1, ou seja, a equação cartesiana do parabolóide permanece como z = x² - e².

2.- Eles são considerados planos paralelos para o plano ZX, ou seja, y = ctte.

3.- Com y = ctte é z = x² - C, que representa parábolas com as ramificações e o vértice abaixo do plano XY.

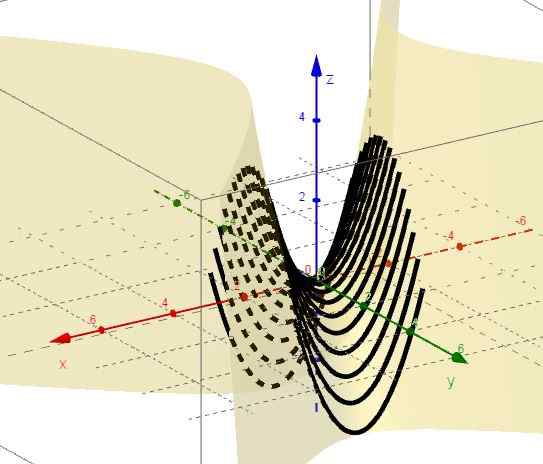Figura 2. Família de curvas z = x² - C. Fonte: f. Zapata através da Geogebra.

4.- Com x = ctte é z = c - y², que representa parábolas com os galhos para baixo e o vértice acima do plano XY.

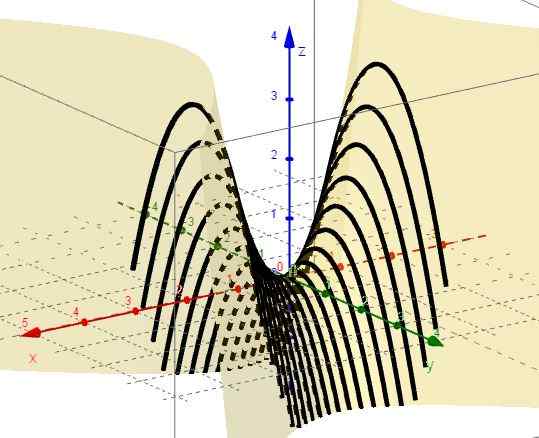Figura 3. Família de curvas z = c - e². Fonte: f. Zapata através da Geogebra.

5.- Com z = ctte é c = x² - e², que representam hiperbolas em aviões paralelos ao avião XY. Quando C = 0 existem duas linhas (A +45º e -45º em relação ao eixo X) que são interceptadas na origem no plano XY.

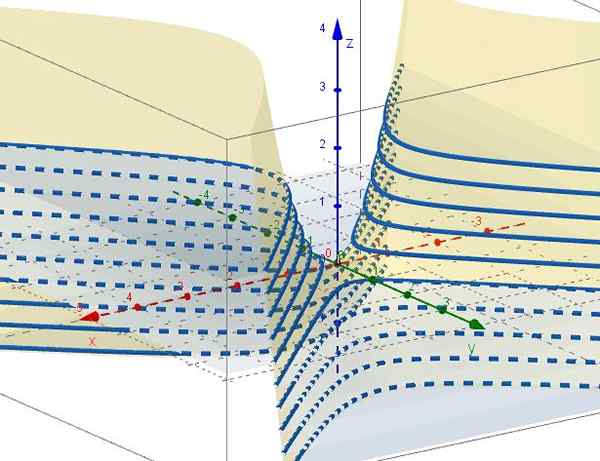Figura 4. Família de curvas x² - e² = C. Fonte: f. Zapata através da geogebra ..

Propriedades de parabolóide hiperbólico

1.- Quatro pontos diferentes no espaço tridimensional definem um e apenas um parabolóide hiperbólico.

Pode atendê -lo: limitar as propriedades (com exemplos)

2.- Parabolóide hiperbólico é um superfície dupla regulada. Isso significa que, apesar de ser uma superfície curva, para cada ponto de um parabolóide hiperbólico, duas linhas diferentes passam completamente para o parabolóide hiperbólico. A outra superfície que não é um avião e é duplamente regulamentada é o Revolução hiperboloide.

É precisamente a segunda propriedade do parabolóide hiperbólico que permitiu um amplo uso na arquitetura, pois a superfície pode ser gerada a partir de vigas ou cordas retas.

A segunda propriedade do parabolóide hiperbólico permite uma definição alternativa: É a superfície que pode ser gerada por uma linha móvel direta paralela a um plano fixo e corta duas linhas fixas que servem como um guia. A figura a seguir esclarece essa definição alternativa de parabolóide hiperbólico:

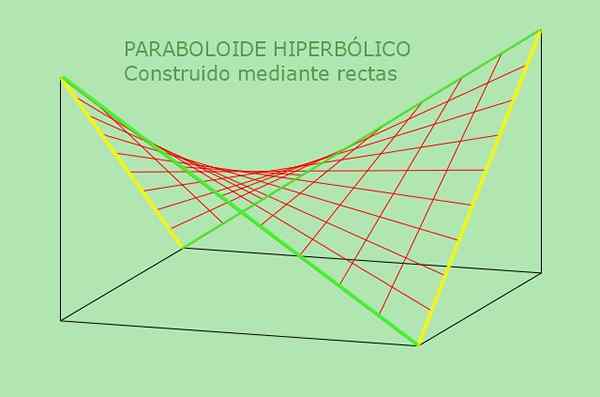Figura 5. O parabolóide hiperbólico é uma superfície duplamente regulamentada. Fonte: f. Zapata.

Exemplos resolvidos

- Exemplo 1

Demonstrar que a equação: Z = xy, corresponde a um parabolóide hiperbólico.

Solução

Uma transformação será aplicada nas variáveis ​​x e y correspondentes a uma rotação dos eixos cartesianos em relação ao z do eixo +45. As antigas coordenadas X e Y são transformadas no novo x 'e e' de acordo com os seguintes relacionamentos:

x = x ' - y'

y = x ' + e'

Enquanto a coordenada z permanece a mesma, ou seja, z = z '.

Substituindo na Equação Z = x e temos:

z '= (x' - y ') (x' + y ')

Ao aplicar o produto notável da diferença pela soma igual à diferença de quadrados, é:

Z '= x'² - e'²

que corresponde claramente à definição inicialmente dada de parabolóide hiperbólico.

A interceptação dos planos paralelamente ao eixo XY com o parabolóide hiperbólico z = x e determina hiperbolas equiláteis que têm assíntotas os planos x = 0 e y = 0.

Pode atendê -lo: Miletus como o teorema

- Exemplo 2

Determine os parâmetros para e b do parabolóide hiperbólico que passa pelos pontos a (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) e D (2, -1, 32/9).

Solução

De acordo com suas propriedades, quatro pontos no espaço tridimensional determinam um único parabolóide hiperbólico. A equação geral é:

Z = (x/a)² - (e B)²

Substituímos os valores fornecidos:

Para o ponto A, você tem 0 = (0/a)² - (0/b)², equação que é satisfeita, independentemente dos valores dos parâmetros A e B.

Substituindo o ponto B é obtido:

5/9 = 1/A² - 1 b²

Enquanto para o ponto C permanece:

32/9 = 4/A² - 1 b²

Finalmente, para o ponto D, é obtido:

32/9 = 4/A² - 1 b²

Que é idêntico à equação anterior. Em resumo, o sistema de equações deve ser resolvido:

5/9 = 1/A² - 1 b²

32/9 = 4/A² - 1 b²

Subtraindo a segunda equação do primeiro é obtida:

27/9 = 3/A² o que implica isso² = 1.

Da mesma forma, a segunda equação do quadruplo do primeiro é subtraída, obtendo:

(32-20)/9 = 4/a² - 4/a² -1 b² + 4/b²

Isso é simplificado como:

12/9 = 3/b² ⇒ b² = 9/4.

Em suma, o parabolóide hiperbólico que passa pelos pontos A, B, C e D dados tem uma equação cartesiana dada por:

Z = x² - (4/9) e²

- Exemplo 3

De acordo com as propriedades do parabolóide hiperbólico, duas linhas que estão completamente contidas nele passam para cada ponto. Para o caso z = x^2 - y^2, encontre a equação das duas linhas que passam pelo ponto P (0, 1, -1) pertencente claramente ao parabolóide hiperbólico, de modo que todos os pontos dessas linhas também pertencem ao mesmo.

Solução

Usando o produto notável da diferença nos quadrados, a equação do parabolóide hiperbólico pode ser escrita da seguinte forma:

Pode servir a você: quadrilateral: elementos, propriedades, classificação, exemplos

(x + y) (x - y) = c z (1/c)

Onde C é uma constante não -zero.

A equação x + y = c z e a equação x - y = 1/c correspondem a dois planos com vetores normais n= y m=. O produto vetorial m x n = A direção da interseção da linha dos dois aviões nos dá. Em seguida, uma das linhas que passa pelo ponto P e pertence ao parabolóide hiperbólico tem uma equação paramétrica:

= + t

Para determinar c, substituímos o ponto P na equação x + y = c z, obtendo:

C = -1

Da mesma forma, mas considerando as equações (x - y = k z) e (x + y = 1/k) você tem a equação paramétrica da linha:

= + s com k = 1.

Em suma, as duas linhas:

= + t y = + s

Eles estão completamente contidos no parabolóide hiperbólico z = x² - e² passando pelo ponto (0, 1, -1).

Como um cheque suponha t = 1 o que nos dá o ponto (1,2, -3) na primeira linha. Você tem que verificar se também está no parabolóide z = x² - e²:

-3 = 1² - 2² = 1 - 4 = -3

Que confirma isso, com efeito, pertence à superfície do parabolóide hiperbólico.

O parabolóide hiperbólico na arquitetura

Figura 6. Oceanográfico de Valência (Espanha).Fonte: Wikimedia Commons.

O parabolóide hiperbólico tem sido usado na arquitetura pelos grandes arquitetos de vanguarda, entre os quais os nomes do arquiteto espanhol Antoni Gaudí (1852-1926) e muito particularmente os espanhóis também os espanhóis Félix Candela (1910-1997) são particularmente particularmente.

Abaixo estão alguns trabalhos baseados no parabolóide hiperbólico:

-Capela da cidade de Cuernavaca (México) Trabalho do arquiteto Félix candela.

-The Oceanographic of Valência (Espanha), também de Félix Candela.

Referências

1. Enciclopédia da matemática. Superfície governada. Recuperado de: Enciclopédia.org
2. Llera Rubén. Parabolóide hiperbólico. Recuperado de: rubenllera.WordPress.com
3. Weisstein, Eric W. “Parabolóide hiperbólico.”De Mathworld-A Wolfram Web Resource. Recuperado de: Mathworld.Volfrâmio.com
4. Wikipedia. Parabolóide. Recuperado de: em.Wikipedia.com
5. Wikipedia. Parabolóide. Recuperado de: é.Wikipedia.com
6. Wikipedia. Superfície governada. Recuperado de: em.Wikipedia.com