Teorema da existência e demonstração, exemplos e exercícios de singularidade

Ele Teorema da existência e singularidade estabelece as condições necessárias e suficientes para uma equação diferencial de primeira ordem, com uma determinada condição inicial, para ter uma solução e que esta solução também é a única. 

No entanto, o teorema não fornece nenhuma técnica ou indicação de como encontrar essa solução. O teorema da existência e singularidade também se estende a equações diferenciais de ordem superior com as condições iniciais, que é conhecida como problema de Cauchy.

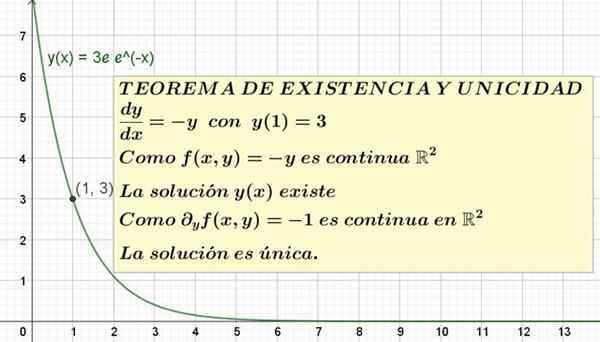
figura 1. Uma equação diferencial com a condição inicial e sua solução é mostrada. O teorema da existência e singularidade garante que é a única solução possível.

A declaração formal do teorema da existência e exclusividade é a seguinte:

"Para uma equação diferencial e '(x) = f (x, y) com condição inicial e (a) = b,  existe pelo menos uma solução em uma região retangular do plano XY contendo o ponto (A, b), Sim f (x, y) É contínuo naquela região. E se o derivado parcial de F em relação à e: G = ∂f/ ∂y É contínuo na mesma região retangular, portanto a solução é única em um ambiente do ponto (A, b) conteúdo na região de continuidade de F e g."

A utilidade desse teorema é o primeiro a saber quais são as regiões do plano XY em que pode haver uma solução e também saber se a solução encontrada é a única possível ou se houver outros. 

Observe que, no caso de a condição de exclusivo.

[TOC]

Demonstração do teorema da existência e exclusividade

Figura 2. Para Charles Émile Picard (1856-1941) Uma das primeiras manifestações do teorema da existência e singularidade é credenciada. Fonte: Wikimedia Commons.

Para este teorema, duas manifestações possíveis são conhecidas, uma delas é a demonstração de Charles Émile Picard (1856-1941) e o outro é devido a Giuseppe Peano (1858-1932) com base nos trabalhos de Augustin Louis Cauchy (1789-1857 ).

Pode atendê -lo: vetores simultâneos: características, exemplos e exercícios

Deve -se notar que as mentes matemáticas mais brilhantes do século XIX participaram da demonstração desse teorema, para que possa ser intuído que nenhum deles seja simples.

Para demonstrar formalmente o teorema, é necessário primeiro estabelecer uma série de conceitos de matemática mais avançados, como funções do tipo Lipschitz, espaços de Banach, Caratheodory e vários outros teorema da existência, que escapam do objetivo do artigo.

Grande parte das equações diferenciais que são tratadas na física lidam com funções contínuas nas regiões de interesse; portanto, nos limitaremos a mostrar a maneira como o teorema é aplicado em equações simples.

Exemplos

- Exemplo 1

Considere a seguinte equação diferencial com uma condição inicial:

e '(x) = - y; com e (1) = 3

Existe uma solução para este problema? É a única solução possível?

Respostas

Primeiro, a existência da solução da equação diferencial é avaliada e que também atende à condição inicial. 

Neste exemplo f (x, y) = - y A condição da existência exige saber se  f (x, y) É contínuo em uma região plana XY contendo o ponto de coordenada x = 1, y = 3.

Mas f (x, y) = -y É o função relacionada, que é contínuo no domínio de números reais e existe em toda a gama de números reais.

Portanto, conclui -se que f (x, y) é contínuo em r², Portanto, o teorema garante a existência de pelo menos uma solução.

Sabendo disso, é hora de avaliar se a solução é única ou se pelo contrário, há mais de um. Para isso, é necessário calcular o derivado parcial de F Sobre a variável e:

∂f/∂y = ∂ (-y)/∂y = -1

Então G (x, y) = -1 que é uma função constante, que também é definida para todos os r² E também é contínuo lá. Segue -se que o teorema da existência e exclusividade garante que esse problema de valor inicial tenha uma solução única, embora não nos diga o que é.

Pode atendê -lo: polígono convexo: definição, elementos, propriedades, exemplos

- Exemplo 2

Considere a seguinte equação diferencial comum de primeira ordem com a condição inicial:

e '(x) = 2√y; e (0) = 0.

Há uma solução e (x) Para este problema? Nesse caso, determine se há um ou mais de um.

Responder

Nós consideramos a função f (x, y) = 2√y. A função F é definido apenas para y≥0, Bem, sabemos que um número negativo não tem raiz real. Além do mais f (x, y) É contínuo no semiplano superior de r²  incluindo o eixo x, então O teorema da existência e exclusividade garante Pelo menos uma solução naquela região.

Agora, a condição inicial x = 0, y = 0 está na borda da região da solução. Então tomamos o derivado parcial de f (x, y) em relação a y:

∂f/∂y = 1/√y

Nesse caso, a função não é definida para y = 0, exatamente onde a condição inicial é.

O que nos diz o teorema? Diz -nos que, embora saibamos que existe pelo menos uma solução, o semiplano superior do eixo x, incluindo o eixo x, pois a condição de singularidade não é atendida, não há garantia de que exista uma única solução.

Isso significa que pode haver uma ou mais de uma solução na região de continuidade de f (x, y). E como sempre, o teorema não nos diz o que poderia ser.

Exercícios resolvidos

- Exercício 1

Resolva o problema Cauchy do Exemplo 1:

e '(x) = - y; com e (1) = 3. 

Encontre a função y (x) que satisfaz a equação diferencial e a condição inicial.

Solução

No Exemplo 1, foi determinado que esse problema tem uma solução e também é único. Para encontrar a solução, a primeira coisa que deve ser notada é que é uma equação diferencial de primeiro grau de variáveis ​​separáveis, que é escrita da seguinte maneira:

Pode servir a você: coeficiente de variação: para que serve, cálculo, exemplos, exercícios

dy /dx = - e → dy = -y dx

Dividindo entre e em ambos os membros para separar as variáveis ​​que temos:

dy/y = - dx

Integral indefinido em ambos os membros é aplicado:

∫ (1/y) dy = - ∫dx

Resolver as integrais indefinidas é:

ln (y) = -x + c

onde C é uma constante de integração que é determinada pela condição inicial:

ln (3) = -1 + c, isto é, que c = 1 + ln (3)

Substituir o valor de C e a reorganização é:

ln (y) - ln (3) = -x + 1

Aplicando a seguinte propriedade dos logaritmos:

A diferença de logaritmos é o logaritmo quociente

A expressão anterior pode ser reescrita assim:

ln (y/3) = 1 - x

A função exponencial é aplicada com os dois membros para obter:

S / 3 = e^{(1 - x)}

Que é equivalente a:

 y = 3e e^-x

Esta é a solução única da equação e '= -y com y (1) = 3. O gráfico desta solução é mostrado na Figura 1.

- Exercício 2

Encontre duas soluções para o problema levantado no Exemplo 2:

e '(x) = 2√ (y); e (0) = 0.

Solução

É também uma equação de variáveis ​​separadas, que é escrita diferencialmente:

Dy / √ (y) = 2 dx

Tomar a integral indefinida em ambos os membros permanece:

2 √ (y) = 2 x + c

Como se sabe que y≥0 Na região da solução que temos:

y = (x + c)² 

Mas como a condição inicial x = 0, y = 0 deve ser atendida, a constante C é zero e a solução a seguir permanece:

e (x) = x².

Mas esta solução não é única, a função y (x) = 0 também é uma solução do problema levantado. O teorema da existência e singularidade aplicado a esse problema no Exemplo 2 já havia previsto que poderia haver mais de uma solução.

Referências

1. Coddington, Earl A.; Levinson, Norman (1955), Teoria das equações diferenciais comuns, Nova York: McGraw-Hill.
2. Enciclopédia da matemática. Teorema de Cauchy-Lipschitz. Recuperado de: Enciclopédia.org
3. Lindelöf, South L'A Aplicação dos sucessivos de Methode des aproximações AUX AUX Equations difírentielles ordenines du premier ordre; Compttes rendus hebdomadaires des Séances de l'annc acadequie des Sciences. Vol. 116, 1894, pp. 454-457. Recuperado de: Gallic.Bnf.fr.
4. Wikipedia. Método de abordagens sucessivas de Picard. Recuperado de: é.Wikipedia.com
5. Wikipedia. Teorema de Picard-Lindelöf. Recuperado de: é.Wikipedia.com.
6. Zill, d.1986. Equações diferenciais elementares com aplicações.Prentice Hall.