Verão telescópico como é resolvido e resolvido exercícios

O Somatório Telescópico É um ramo de operações com série numérica. Aborda os resumos dos elementos de um valor inicial a "n" de expressões cujo argumento se deve a qualquer um dos seguintes padrões:

(F_x - F_x+1); F_x+1  - F_x)

Onde sua expressão sumária é definida da seguinte maneira: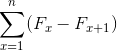

Como também:

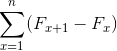
Fonte: Pixabay.com

Eles representam uma soma de elementos que, ao desenvolver, estão sujeitos a cancelamentos de termos opostos. Causando a seguinte igualdade para sumões telescópicas:

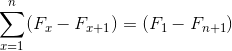
Seu nome vem do relacionamento com o aparecimento de um telescópio clássico, que pode ser dobrado e implantado, mudando significativamente sua dimensão. Da mesma forma, as sumaturas telescópicas, que, por sua natureza, são infinitas, podem ser resumidas na expressão simplificada:

F₁ - F_N+1

[TOC]

Demonstração

Ao desenvolver a soma dos termos, a eliminação de fatores é bastante óbvia. Onde para cada um dos casos, elementos opostos aparecerão na seguinte iteração.

O primeiro caso será tomado como exemplo (f_x - F_x+1), como o processo funciona homólogo de (f_x+1-F_x).

Desenvolvendo os 3 primeiros valores 1, 2, 3 A tendência de simplificação é observada

X₁     (F₁ - F₁₊₁) = F₁ - F₂

X₂     (F₂ - F₂₊₁) = F₂ - F₃

X₃     (F₃ - F₃₊₁) = F₃ - F₄

Onde expressando a soma dos elementos descritos:

X₁ + X₂ + X₃ = F₁ - F₂ + F₂ - F₃ + F₃ - F₄

Observa -se que os termos f₂ e f₃ Eles são descritos com seus opostos, o que torna sua simplificação inevitável. Da mesma maneira, observa -se que os termos f₁ e f₄ se mantém.

Se a soma foi feita de x = 1 a x = 3, significa que o elemento f₄ corresponde ao termo genérico f_N+1.

Demonstrando assim igualdade:

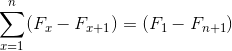
Como é resolvido?

O objetivo das somaes telescópicas é facilitar o trabalho, para que não seja necessário desenvolver uma quantidade infinita de termos ou simplificar uma cadeia muito longa.

Pode servir a você: Método Trachtenberg: O que é, exemplos

Para resolução, só será necessário avaliar os termos f₁ e f_N+1. Essas substituições simples compõem o resultado final da soma.

A totalidade dos termos não será expressa, tornando -se necessária para a demonstração do resultado, mas não para o processo de cálculo normal.

O importante é notar a convergência da série numérica. Às vezes, o argumento da soma não será expresso de maneira telescópica. Nesses casos, a implementação de métodos de fatoração alternativa é muito comum.

O método de fatorização característica nos resumos telescópicos é o de frações simples. Isso ocorre quando uma fração original se decompõe em uma soma de várias frações, onde o padrão telescópico pode ser observado (f_x - F_x+1) ou (f_x+1  - F_x).

Decomposição em frações simples

Para verificar a convergência da série numérica, é muito comum transformar expressões racionais com o método de frações simples. O objetivo é modelar o argumento até a forma de uma soma telescópica.

Por exemplo, a seguinte igualdade representa uma decomposição em frações simples:

Ao desenvolver a série numérica e aplicar as propriedades correspondentes que a expressão leva a seguir:

Onde a forma telescópica pode ser vista (f_x - F_x+1).

O procedimento é bastante intuitivo e consiste em encontrar os valores do numerador que, sem quebrar a igualdade, permitem separar os produtos que estão no denominador. As equações que surgem na determinação desses valores são levantadas de acordo com as comparações entre os dois lados da igualdade.

Este procedimento é observado passo a passo no desenvolvimento do Exercício 2.

Pode atendê -lo: 6 enigmas matemáticos divertidos para crianças

História

É bastante incerto poder definir o momento histórico em que as sumões telescópicas foram apresentadas. No entanto, sua implementação começa a ser vista no século XVII, em estudos numéricos da série realizada por Leibniz e Huygens.

Ambos os matemáticos, ao explorar as sumões de números triangulares, começam a observar as tendências na convergência de certas séries de elementos sucessivos. Mas ainda mais interessante é o começo da modelagem dessas expressões, em elementos que não acontecem necessariamente.

De fato, a expressão usada anteriormente para se referir a frações simples:

Foi apresentado por Huygens e imediatamente chamou a atenção de Leibniz. Quem com o tempo pode observar a convergência em valor 2. Sem saber, ele implementou o somatismo telescópico.

Exercícios

Exercício 1

Defina qual termo a soma a seguir converge:

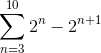
Quando a soma é desenvolvida manualmente, o seguinte padrão é observado:

(2³ - 2⁴) + (2⁴ - 2⁵) + (2⁵ - 2⁶)… (2¹⁰ - 2^onze)

Onde os fatores de 2⁴ até 2¹⁰ Eles apresentam partes positivas e negativas, tornando seu cancelamento evidente. Então os únicos fatores que não serão simplificados serão os primeiros “2³"E o último" 2^onze".

Dessa forma, ao implementar os critérios telescópicos de resumo, é obtido:

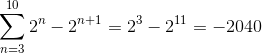
Exercício 2

Transforme o argumento em uma soma do tipo telescópico e defina a convergência da série:

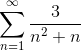
Conforme indicado na declaração, a primeira coisa será decompor em frações simples, a fim de repensar o argumento e expressá -lo de forma telescópica.

2 frações cujos denominadores são respectivamente "n" e "n+1" devem ser encontrados, onde o método usado abaixo deve atingir os valores do numerador que atendem à igualdade.

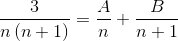
Os valores de A e B são definidos. A primeira soma das frações é feita.

Pode atendê -lo: 60 divisores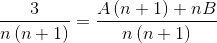

Então, os denominadores são simplificados e uma equação linear é estabelecida.

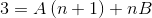
Na próxima etapa, a expressão da direita é operada, até um padrão comparável ao "3" à esquerda.

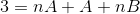
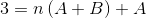
Para definir as equações a serem usadas, os resultados de ambos os lados da igualdade devem ser comparados. Ou seja, nenhum valores variáveis ​​de n são observados no lado esquerdo, dessa maneira A +B terá que ser igual a zero.

A + b = 0; A = -b

Por outro lado, o valor constante terá que ser igual ao valor constante 3.

A = 3

Portanto.

A = 3 e b = -3

Já definiu os valores do numerador para frações simples, a soma está repensando.

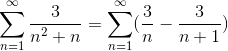
Onde a forma genérica de soma telescópica já foi alcançada. A série telescópica é desenvolvida.

Onde, dividindo -se por um número muito grande, o resultado se aproximará cada vez mais, observando a convergência da série em valor 3.

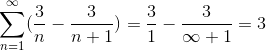
Esse tipo de série não pôde ser resolvido em outras palavras, devido à quantidade infinita de iterações que definem o problema. No entanto, esse método, juntamente com muitos outros, enquadram o ramo do estudo da série numérica, cujo objetivo é determinar os valores de convergência ou definir a divergência dessas séries.

Referências

1. Lições de cálculo infinitesimal. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. Editum, 1994.
2. Cálculo abrangente: sucessões e série de funções. Antonio Rivera Figueroa. Patria Editorial Group, 21 de outubro. 2014.
3. Um curso em cálculo e análise real. Sudhir r. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 de junho. 2006.
4. Série Infinita. Forte Tomlinson. The Clarendon Press, 1930.
5. Elementos da teoria das procissões infinitas. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorgan, 1923.