Sistema octal

O que é um sistema octal?

Ele Sistema octal É um sistema de numeração de base oito (8); Ou seja, consiste em oito dígitos, que são: 0, 1, 2, 3, 4, 5, 6 e 7. Portanto, cada dígito de um número octal pode ter qualquer valor de 0 a 7. Os números octais são formados a partir de números binários.

Isso ocorre porque sua base é um poder exato de dois (2). Ou seja, os números que pertencem ao sistema octal são formados quando são agrupados em três dígitos consecutivos, ordenados da direita para a esquerda, obtendo assim seu valor decimal.

História do sistema octal

O sistema octal tem sua origem nos tempos antigos, quando as pessoas usavam as mãos para contar oito por oito animais.

Por exemplo, para contar o número de vacas em um estábulo, a mão direita começou a ter o polegar com o dedo mindinho; Então, para contar o segundo animal, o polegar se juntou ao dedo indicador, e assim por diante com os dedos restantes de cada mão, até concluir 8.

Existe a possibilidade de que o sistema de numeração octal antes do decimal possa contar os espaços interdigitais; isto é, conte todos os dedos, exceto os polegares.

Posteriormente, foi estabelecido o sistema de numeração octal, originado do sistema binário, porque precisa de muitos dígitos para representar apenas um número; A partir de então, os sistemas octal e hexagonal foram criados, que não requerem tantos dígitos e que podem facilmente converter para o sistema binário.

Sistema de numeração octal

O sistema octal consiste em oito dígitos que variam de 0 a 7. Eles têm o mesmo valor que no caso do sistema decimal, mas seu valor relativo muda dependendo da posição que estes ocupam. O valor de cada posição é dado pelos poderes base 8.

Pode atendê -lo: Regra T: Características, para que sejam, exemplos

As posições dos dígitos em um número octal têm os seguintes pesos:

8⁴, 8³, 8², 8¹, 8⁰, Octal Point, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

O principal dígito octal é 7; Dessa forma, quando contado neste sistema, uma posição de um dígito de 0 a 7 está aumentando. Quando atinge 7, é reciclado em 0 para a próxima contagem; Isso aumenta a seguinte posição de dígito. Por exemplo, para contar sequências, no sistema octal, será:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Existe um teorema fundamental que é aplicado ao sistema octal e é expresso da seguinte maneira:

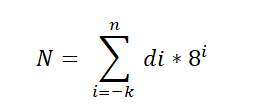
Nesta expressão, Di representa o dígito multiplicado pela potência da base 8, que indica o valor posicional de cada dígito, da mesma maneira que é ordenada no sistema decimal.

Por exemplo, você tem o número 543.2. Para levá -lo ao sistema octal, ele se decompõe o seguinte:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_d

Dessa forma, você tem 543.2_q = 354,25_d. O subscrito que indica que é um número octal que também pode ser representado pelo número 8; e o subscrito D refere -se ao número decimal, que também pode ser representado com o número 10.

Conversão do sistema octal em decimal

Para converter um número de sistema octal em seu equivalente no sistema decimal, cada dígito octal deve ser multiplicado por seu valor posicional, começando pela direita.

Exemplo 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Pode atendê -lo: igualdade matemática

Exemplo 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0,125)

26.9₈ = 16 + 6 + 1,125

26.9₈= 23.125₁₀

Conversão decimal do sistema para octal

Um número inteiro decimal pode ser convertido em um número octal usando o método de divisão repetido, onde o número inteiro decimal é dividido por 8 até que o quociente seja igual a 0, e o desperdício de cada divisão representará o número octal.

O lixo é ordenado do último ao primeiro; isto é, o primeiro resíduo será o dígito menos significativo do número octal. Dessa forma, o dígito mais significativo será o último resíduo.

Exemplo

Octal do número decimal 266₁₀

- O número decimal 266 é dividido por 8 = 266/8 = 33 + 2 resíduos.

- Então o 33 é dividido por 8 = 33/8 = 4 + 1 resíduo.

- 4 é dividido por 8 = 4/8 = 0 + 4 resíduos.

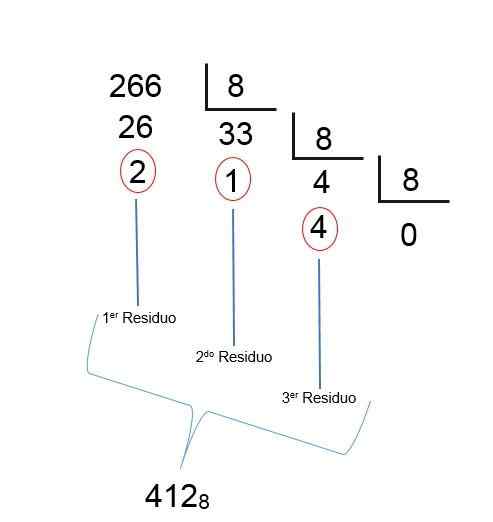
Como na última divisão, um quociente menor que 1 é obtido, isso significa que o resultado foi encontrado; Somente os restos mortais devem ser ordenados ao contrário, para que o número octal de 266 decimal seja 412, como pode ser visto na seguinte imagem:

Conversão do sistema octal binário

A conversão do sistema octal em binária é realizada ao converter o dígito octal em seu dígito binário equivalente, formado por três dígitos. Há uma tabela que mostra como os oito dígitos possíveis se tornam:

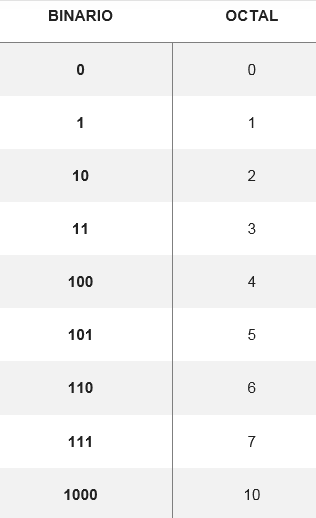
A partir dessas conversões, você pode alterar qualquer número do sistema octal para binário, como converter o número 572₈ Seus equivalentes são procurados na mesa. Assim, você tem que:

5₈ = 101

7₈= 111

2₈ = 10

Portanto, 572₈ equivalente no sistema binário para 10111110.

Sistema binário para conversão octal

O processo de conversão de números integrais em números inteiros octais é a operação reversa para o processo anterior.

Pode atendê -lo: quais são os elementos de um ângulo?

Ou seja, os bits de números binários são agrupados em dois grupos de três bits, começando da direita para a esquerda. Então, a conversão binária para octal é feita com a tabela anterior.

Em alguns casos, o número binário não terá grupos de 3 bits; Para completá -lo, um ou dois zeros são adicionados à esquerda do primeiro grupo.

Por exemplo, para alterar o número binário 11010110 para octal, é feito o seguinte:

- Grupos de 3 bits são formados a partir da direita (última bit):

11010110

- Como o primeiro grupo está incompleto, um zero é adicionado à esquerda:

011010110

- A conversão é feita da tabela:

011 = 3

010 = 2

110 = 6

Dessa maneira, o número binário 011010110 é equivalente a 326₈.

Conversão do sistema octal em hexadecimal e vice -versa

Para alterar um número octal para o sistema hexadecimal ou hexadecimal para octal, é necessário que o número seja primeiro binário e depois para o sistema desejado.

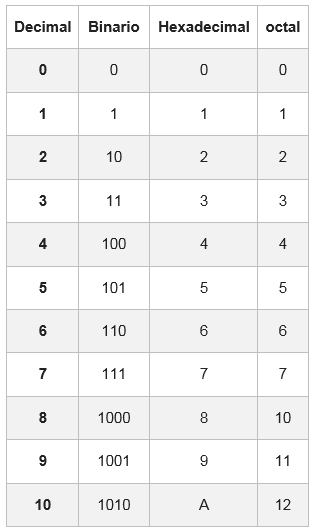
Para isso, há uma tabela em que cada dígito hexadecimal é representado com sua equivalência no sistema binário, composto por quatro dígitos.

Em alguns casos, o número binário não terá grupos de 4 bits; Para completá -lo, um ou dois zeros são adicionados à esquerda do primeiro grupo

Exemplo

Converta o número octal de 1646 em um número hexadecimal:

- O número octal a binário se torna

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Assim, 1646₈ = 1110100110.

- Para converter de binário para hexadecimal, eles são ordenados pela primeira vez em um grupo de 4 bits, começando da direita à esquerda:

11 1010 0110

- O primeiro grupo é concluído com zeros, para que possa ter 4 bits:

0011 1010 0110

- A conversão hexadecimal do sistema binário é feita. As equivalências são substituídas por meio da tabela:

0011 = 3

1010 = a

0110 = 6

Dessa forma, o número octal de 1646 é equivalente a 3A6 no sistema hexadecimal.