Semicircle como calcular o perímetro, área, centróide, exercícios

Ele semicírculo É uma figura plana delimitada por um diâmetro da circunferência e um dos dois arcos circulares planos determinados pelo referido diâmetro.

Dessa forma, um semicírculo é delimitado por um semicircumferência, que consiste em um arco circular plano e um segmento reto que se junta às extremidades do arco circular plano. O semicírculo cobre o semicírculo e todo o interior aponta para o mesmo.

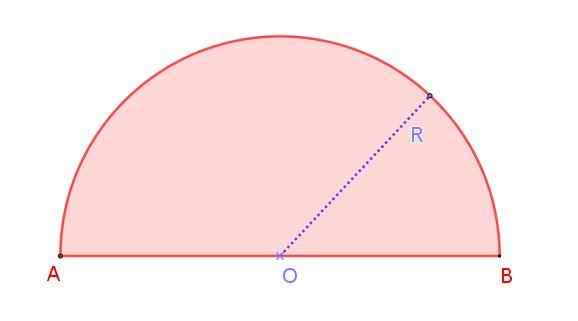figura 1. Radio R Radio Semicircle. Fonte: f. Zapata.

Podemos ver isso na Figura 1, que mostra uma rádio rión r, cuja medida é metade do diâmetro AB. Observe que, diferentemente de um círculo, no qual existem diâmetros infinitos, no semicírculo há apenas um diâmetro.

O semicírculo é uma figura geométrica com muitos usos em arquitetura e design, como vemos na imagem a seguir:

Figura 2. Seminicírculo como um elemento decorativo em arquitetura. Fonte: Pikist.

[TOC]

Elementos e medidas de um semicírculo

Os elementos de um semicírculo são:

1.- O arco circular plano A⌒b

2.- O segmento [AB] 

3.- O interior aponta para o semicírculo composto pelo arco e segmento A⌒b [AB].

Perímetro de um semicírculo

O perímetro é a soma do contorno do arco mais o do segmento direto, portanto:

Perímetro = comprimento do arco a⌒b + comprimento do segmento [ab]

No caso de um semicírculo de rádio, seu perímetro P será dado pela fórmula:

P = π⋅r + 2⋅r = (π + 2) ⋅r

O primeiro termo é metade do perímetro de uma circunferência do raio r, enquanto o segundo é o comprimento do diâmetro, que é o dobro do raio.

Pode atendê -lo: escalas termométricas

Área de um semicírculo

Como um semicírculo é um dos setores angulares planos que permanecem desenhando um diâmetro através da circunferência, sua área A será metade da área do círculo que contém o Radio Semicircle R:

A = (π⋅r²) / 2 = ½ π⋅r²

Centróide de um semicírculo

O centróide de um semicírculo está em seu eixo de simetria a uma altura medida a partir de seu diâmetro de 4/(3π) vezes o raio r.

Isso corresponde a aproximadamente 0,424⋅R, medido no centro do semicírculo e em seu eixo de simetria, como mostrado na Figura 3.

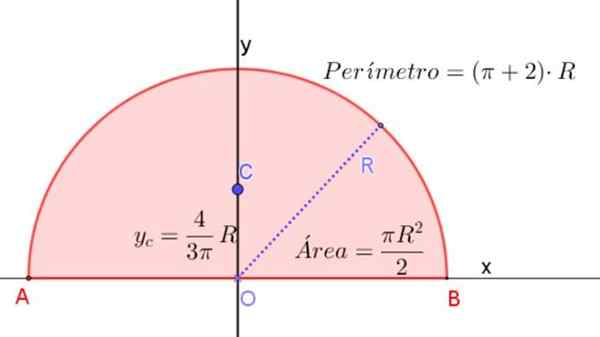Figura 3. Semicírculo da Radio R, indicando as fórmulas para determinar a área, o perímetro e a localização do seu centróide. Fonte: f. Zapata.

Momento de inércia de um semicírculo

O momento de inércia de uma figura plana é definido em relação a um eixo, por exemplo, eixo x, como:

A integral do quadrado da distância dos pontos que pertencem à figura ao eixo, sendo o diferencial de integração uma área infinitesimal da área, tomada na posição de cada ponto. 

A Figura 4 mostra a definição do momento da inércia i_x do semicírculo da Rádio R, com relação ao eixo X que passa por sua diagonal:

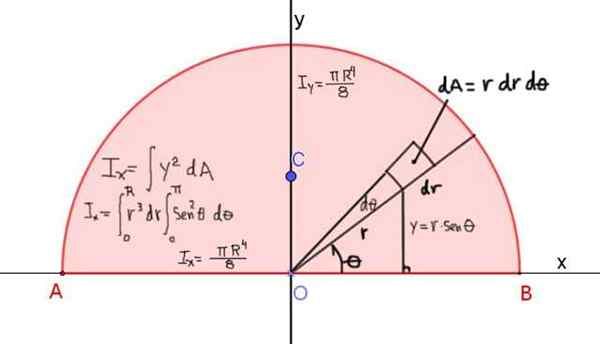Figura 4. Definição de momento de inércia ix de um semicírculo em relação ao eixo x que passa por sua diagonal. O resultado é mostrado para os momentos de inércia em relação aos eixos X e Y. Fonte: f. Zapata.

O momento da inércia em relação ao eixo x é dado por:

Yo_x = (π⋅r⁴) / 8

E o momento da inércia em relação ao eixo de simetria e é:

Pode atendê -lo: Óptica ondulada

Iy = (π⋅r⁴) / 8

Isso mostra que ambos os momentos de inércia coincidem em sua fórmula, mas é importante enfatizar que eles são referidos a eixos diferentes.

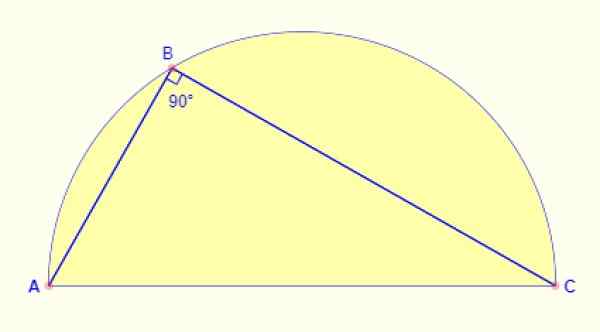
Ângulo registrado

O ângulo registrado no semicírculo é sempre 90º. Independentemente de qual parte do arco é levada ao ponto, o ângulo formado entre os lados AB e BC da figura é sempre reto.

Figura 5. Ângulo registrado no semicírculo. Fonte: Math Open Reference.

Exercícios resolvidos

Exercício 1 

Determinar o perímetro de um raio de 10 cm semicírculo.

Solução

Lembre -se de que o perímetro, dependendo do raio, é dado pela fórmula que vimos anteriormente:

P = (2 + π) ⋅r

P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Exercício 2

Encontre a área de um semicírculo de rádio de 10 cm.

Solução

A fórmula para a área de um semicírculo é:

A = ½ π⋅r² = ½ π⋅ (10cm)² = 50π cm² = 50 x 3,14 cm² = 157 cm².

Exercício 3

Determine a altura H do centróide de um raio semicírculo r = 10 cm medido a partir de sua base, sendo o mesmo o diâmetro do semicírculo. 

Solução

O centróide é o ponto de equilíbrio semicírculo e sua posição está no eixo de simetria a uma altura H da base (diâmetro semicírculo):

H = (4⋅r) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4.246 cm

Exercício 4

Encontre o momento de inércia de um semicírculo em relação ao eixo que coincide com seu diâmetro, sabendo que o semicírculo é feito de uma folha fina. Seu raio é de 10 cm e sua massa é de 100 gramas.

Solução

A fórmula que dá o momento de inércia do semicírculo é:

Pode atendê -lo: física de estado sólido: propriedades, estrutura, exemplos

Yo_x = (π⋅r⁴) / 8

Mas como o problema nos diz que é um semicírculo material, o relacionamento anterior deve ser multiplicado pela densidade da superfície da massa semicírculo, que será denotada por σ.

Yo_x = σ (π⋅r⁴) / 8

Em seguida, determinamos σ, o que não é nada além da massa do semicírculo dividido entre a área do mesmo.

A área foi determinada no Exercício 2 e o resultado foi de 157 cm². Então a densidade superficial deste semicírculo será:

σ = 100 gramas / 157 cm² = 0,637 g/cm²

Então, o momento da inércia em relação ao diâmetro será calculado da seguinte forma:

Yo_x = (0,637 g/cm²) [3.1416 ⋅ (10cm)⁴]/ 8

Resultando:

Yo_x = 2502 g⋅cm²

Exercício 5

Determine o momento de inércia de um raio semicírculo 10 cm construído de uma folha de material com uma densidade de superfície de 0,637 g/cm² por um eixo que passa pelo seu centróide e é paralelo ao seu diâmetro.

Solução

Para resolver este exercício, é necessário lembrar o teorema de Steiner em momentos de inércia de eixos paralelos, que diz:

O momento da inércia i em relação a um eixo que está a uma distância H do centróide é igual à soma do momento da inércia i_c Em relação a um eixo que passa pelo centróide e é paralelo ao primeiro a mais o produto da massa através do quadrado da separação dos dois eixos.

I = i_c + M h²

No nosso caso, sabe -se que é o momento da inércia em relação ao diâmetro, que já foi calculado no Exercício 4. H também sabe entre o diâmetro e o centróide, que foi calculado no Exercício 3.

Nós apenas temos que limpar o IC:

Yo_c = I - m h²

Yo_c = 2502 g⋅cm² - 100g ⋅ (4.246 cm)² resultando no momento da inércia por um eixo paralelo ao diâmetro e que passa pelo centróide é: 

Yo_c = 699,15 G⋅cm²

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Math Open Reference. Semicírculo. Recuperado de: MathpenRef.com.
3. Fórmulas do Universo.Semicírculo. Recuperado de: universoformulas.com.
4. Fórmulas do Universo. Área de um semicírculo. Recuperado de: universoformulas.com.
5. Wikipedia. Semicírculo. Recuperado de: em.Wikipedia.com.