Regra de Sarrus

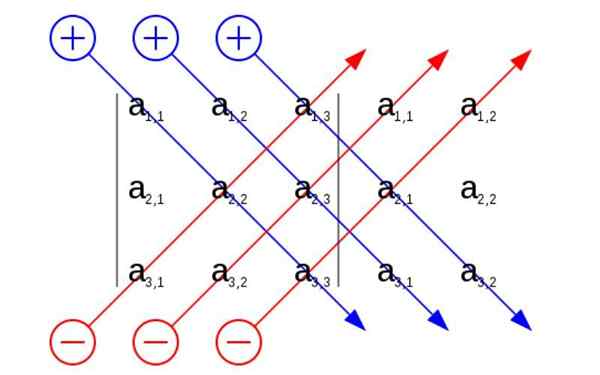
Regra de Sarrus. Fonte: Usuário: Sevela.P, CC BY-SA 4.0, Wikimedia Commons

Qual é a regra de Sarrus?

O Regra de Sarrus É uma técnica calcular determinantes de uma matriz quadrada de 3 × 3 ou mais. Este sistema permite que a solução seja mais facilmente. Também é usado para determinar se os conjuntos de vetores são linearmente independentes e formam a base do espaço vetorial.

Essas aplicações são baseadas na invertibilidade das matrizes. Se uma matriz é regular, seu determinante é diferente de 0. Se for singular, seu determinante vale 0. Os determinantes só podem ser calculados em matrizes quadradas.

Para calcular matrizes de qualquer ordem, o teorema de Laplace pode ser usado. Este teorema nos permite simplificar as matrizes de altas dimensões, em somas de pequenos determinantes que quebramos da matriz principal.

Afirma que o determinante de uma matriz é igual à soma dos produtos de cada linha ou coluna, pelo determinante de sua matriz anexada.

Isso está reduzindo os determinantes, para que um determinante do grau n se torne determinantes de N-1. Se aplicarmos esta regra de maneira sucessiva, podemos obter determinantes da dimensão 2 (2 × 2) ou 3 (3 × 3), onde seu cálculo é muito mais fácil.

Regra de Sarrus

Pierre Frederic Sarrus (1798-1861) era um matemático francês. A maioria de seus tratados matemáticos é baseada em métodos de resolução de equações e no cálculo de variações, dentro de equações numéricas.

Em um de seus tratados, ele resolveu um dos enigmas mais complexos da mecânica. Para resolver os problemas das peças articuladas, Sarrus introduziu a transformação de movimentos retilíneos alternativos, em movimentos circulares uniformes. Este novo sistema é conhecido como o mecanismo de Sarrus.

Pode atendê -lo: externalização e internalização dos custos

A pesquisa que mais lhe deu foi aquela em que ele introduziu um novo método de cálculo dos determinantes, no artigo “Nouvelles Metodes derramaram a respiração des Équations” (“Novo método para a resolução das equações”), publicado em 1833. Essa maneira de resolver equações lineares é conhecida como regra de Sarrus.

A regra de Sarrus permite calcular o determinante de uma matriz 3 × 3, sem usar o teorema de Laplace, introduzindo um método muito mais simples e intuitivo. 

Para poder verificar o valor da regra de Sarrus, tomamos qualquer matriz da dimensão 3:

O cálculo de seu determinante seria feito pelo produto de suas diagonais principais, subtraindo o produto das diagonais inversas. Isso seria o seguinte:

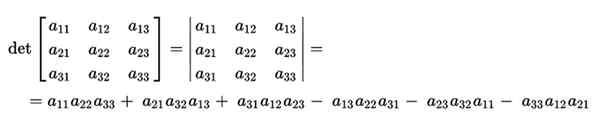
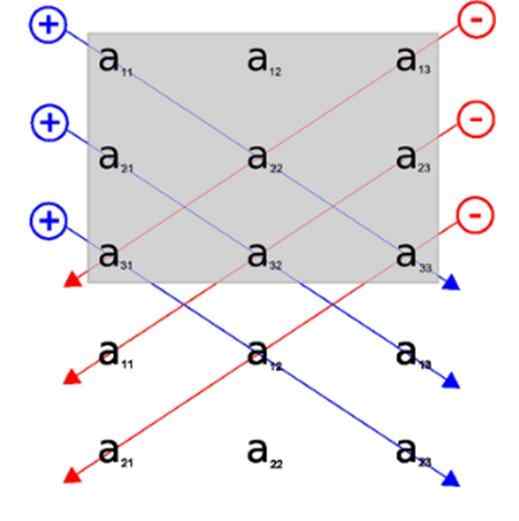
A regra de Sarrus nos permite obter uma visão muito mais simples ao calcular as diagonais do determinante. Seria simplificado adicionando as duas primeiras colunas na parte traseira da matriz.

Dessa forma, é mais claro sobre suas diagonais principais e que o inverso, para o cálculo do produto.

Através desta imagem, podemos ver a aplicação da regra de Sarrus, incluímos a linha 1 e 2, sob a representação gráfica da matriz inicial. Dessa forma, as principais diagonais são as três diagonais que aparecem em primeiro lugar.

Os três diagonais inversos, por sua vez, são aqueles que aparecem primeiro na parte de trás.

Dessa maneira, os diagonais aparecem de uma maneira mais visual, sem complicar a resolução do determinante, tentando descobrir quais elementos da matriz pertencem a cada diagonal.

Pode atendê -lo: Palavras de Quechua traduzidas para o espanhol

Como aparece na imagem, escolhemos as diagonais e calculamos o produto resultante de cada função. Os diagonais que aparecem em azul são aqueles que somam. Para a soma destes, subtraímos o valor das diagonais que aparecem em vermelho.

Para que a compactação seja mais fácil, podemos usar um exemplo numérico, em vez de usar termos algébricos e termos subternos.

Se tomarmos qualquer matriz 3 × 3, por exemplo:

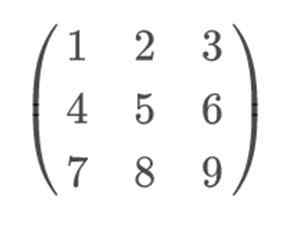
Para aplicar a regra de Sarrus e resolvê -la de uma maneira mais visual, devemos incluir as linhas 1 e 2, como linha 4 e 5, respectivamente. É importante manter a linha 1 na 4ª posição e a linha 2 no 5º. Como se os trocarmos, a regra de Sarrus não será eficaz.

Para calcular o determinante, nossa matriz seria a seguinte:

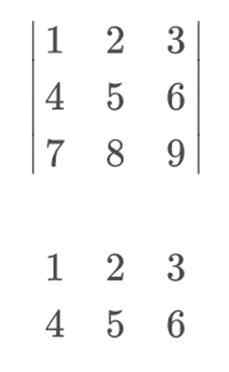
Para continuar com o cálculo, multiplicaremos os elementos das diagonais principais. A descendência que eles começam à esquerda terá um sinal positivo, enquanto os diagonais reversos, que são os que começam à direita, carregam um sinal negativo.

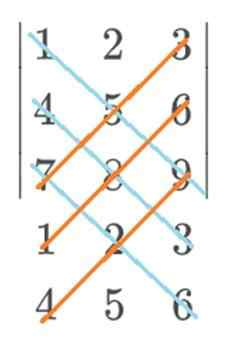
Neste exemplo, o azul iria com um sinal positivo e o vermelho com um sinal negativo. O cálculo final da regra de Sarrus permaneceria desta maneira:

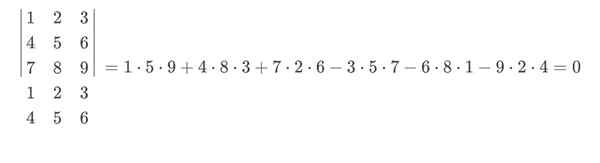
Pessoal de determinantes

Determinante da dimensão 1

Se a dimensão da matriz for 1, a matriz é dessa maneira: a = (a)

Portanto, seu determinante seria o seguinte: det (a) = | a | = a

Resumido, o determinante da matriz A é igual ao valor absoluto da matriz A, que neste caso é um.

Dimension Determinante 2

Se formos para as matrizes da dimensão 2, obtemos matrizes do tipo:

Pode servir você: taumaticgy

Onde seu determinante é definido como:

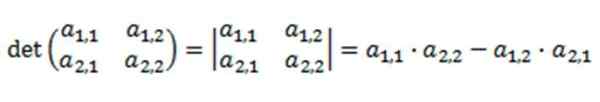
A resolução deste determinante é baseada na multiplicação de sua principal diagonal, subtraindo o produto de sua diagonal inversa.

Determinante da dimensão 3

Se a dimensão da matriz for 3, a matriz resultante seria desse tipo:

O determinante desta matriz seria resolvido através da regra de Sarrus dessa maneira:

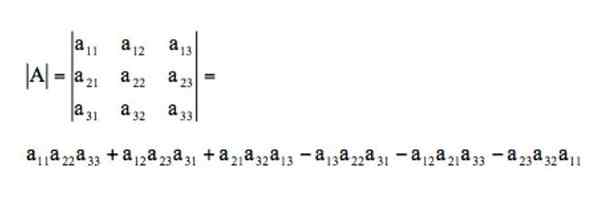
Referências

1. Anthony Nicolaides (1994). Determinantes e matrizes. Pass Publicação.
2. M. Casteleiro Villalba (2004). Introdução à álgebra linear. Editorial ESIC.