Conceito de Redes Bravais, características, exemplos, exercícios

As Redes Bravais Eles são o conjunto de quatorze células unitárias tridimensionais nas quais os átomos de um cristal. Essas células consistem em um arranjo tridimensional de pontos que formam uma estrutura básica que é repetida periodicamente nas três direções espaciais.

A origem dessa denominação para estruturas cristalinas básicas vem de 1850, quando Auguste Bravais mostrou que existem apenas 14 células unitárias tridimensionais básicas possíveis possíveis.

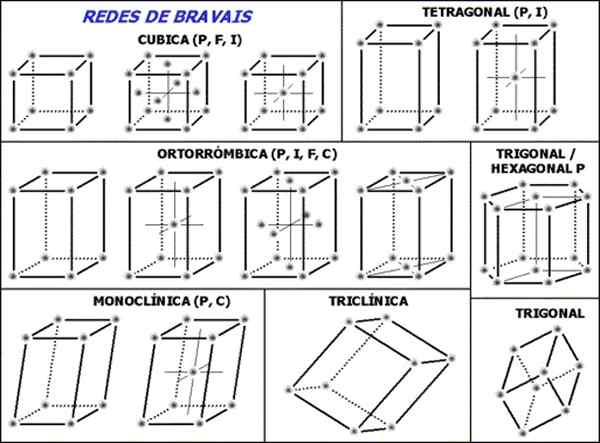
figura 1. As redes Bravais são o conjunto das 14 células unitárias necessárias e suficientes para descrever qualquer estrutura cristalina. (Wikimedia Commons)

O conjunto das 14 redes Bravais é subdividido em sete grupos ou estruturas de acordo com a geometria das células, esses sete grupos são:

1- cúbico

2- tetragonal

3- ortorrombic

4- trigonal-hexagonal

5-monoclínico

6- triclínico

7- trigonal

Cada uma dessas estrutura define uma célula unitária, sendo esta a menor porção que retém o arranjo geométrico de átomos no vidro.

[TOC]

Características das redes Bravais

Os quatorze redes de Bravais, como afirmado acima, são subdivididos em sete grupos. Mas cada um desses grupos possui suas células unitárias com seus parâmetros característicos que são:

1- O parâmetro de rede (a, b, c)

2- Número de átomos por célula

3- relação entre parâmetro de rede e rádio atômico

4- Número de coordenação

5- fator de embalagem

6- Espaços intersticiais

7- por traduções ao longo dos vetores a, b, c a estrutura cristalina é repetida.

Redes cúbicas

Consiste na rede cúbica simples ou cúbica, a rede cúbica centrada em faces ou na rede cúbica F e a rede cúbica centrada no corpo ou rede cúbica.

Todas as redes cúbicas têm os três Parâmetros de rede correspondente aos endereços x, y, z do mesmo valor:

A = b = c

Rede cúbica p

É conveniente destacar que os átomos são representados por esferas cujos centros estão nos vértices da célula cúbica P.

Pode atendê -lo: satélites artificiais

No caso da rede cúbica P o Número de átomos por célula É 1, porque em cada vértice apenas a oitava parte do átomo está dentro da célula unitária, então 8*⅛ = 1.

Ele Número de coordenação Indica o número de átomos que são vizinhos próximos na rede cristalina. No caso da rede cúbica p, o número de coordenação é 6.

Rede cúbica i

Nesse tipo de rede, além dos átomos nos vértices do cubo, há um átomo no centro do cubo. Então número de átomo por célula Unitário na rede cúbica P é 2 átomos.

Figura 2. Rede cúbica centrada no corpo.

Rede cúbica f

É a rede cúbica que, além dos átomos nos vértices, tem um átomo no centro da face de cada cubo. Ele Número de átomos por célula É 4, já que cada um dos seis átomos da face tem metade dentro da célula é dizer 6*½ = 3 mais 8*⅛ = 1 nos vértices.

Figura 3. Rede cúbica centrada em rostos.

Rede hexagonal

Nesse caso, a célula unitária é um prisma hexagonal reto. Redes hexagonais têm os três Parâmetros de rede correspondente cumprindo o seguinte relacionamento:

A = b ≠ c

Sendo o ângulo entre o vetor A e B de 120º, como mostrado na figura. Enquanto entre os vetores A e C, bem como entre B e C são ângulos retos.

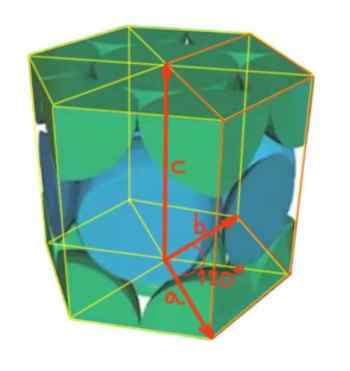Figura 4. Rede hexagonal.

Ele Número de átomos por célula Será calculado da seguinte forma:

- Em cada uma das 2 bases do prisma hexagonal, existem 6 átomos nos seis vértices. Cada um desses átomos ocupa ⅙ da célula unitária.

- No centro de cada uma das 2 bases hexagonais, há 1 átomo que ocupa 1/2 célula unitária.

- Nas 6 faces laterais do prisma hexagonal, existem 3 átomos, cada um dos quais ocupa ⅔ da célula unitária e 3 átomos que ocupam cada ⅓ de volume da célula unitária.

Pode atendê -lo: ouvir força: forças de superfície e massa

(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6 

A relação entre os parâmetros da rede A e B com o raio atômico R sob a suposição de que todos os átomos são de rádio igual e estão em contato é: 

a/r = b/r = 2

Exemplos

Os metais são os principais exemplos de estruturas cristalinas e também as mais simples, porque geralmente consistem em um único tipo de átomo. Mas existem outros compostos não metálicos que também formam estruturas cristalinas, como diamante, quartzo e muitos outros.

- O ferro

O ferro possui uma célula unitária cúbica simples com parâmetro de rede ou borda a = 0,297 nm. Em 1 mm, existem 3,48 x 10^6 células unitárias.

- O cobre

Possui uma estrutura cristalina cúbica centrada em faces, formada apenas por átomos de cobre.

- Gemas preciosas

Gemas preciosas são estruturas cristalinas basicamente o mesmo composto, mas com pequenas porções de impurezas que geralmente são responsáveis ​​pela cor deles.

Diamante

É composto apenas de carbono e não contém impurezas, e é por isso que não tem cor. O diamante tem Estrutura cristalina cúbica (isométrica-hexoctahedral) e é o material mais difícil conhecido.

Quartzo

É composto de sílica óxido, geralmente é incolor ou branco. Sua estrutura cristalina é trigonal-trapezoédrica.

Rubi 

É composto de óxido de alumínio com impurezas cromadas que dão sua cor vermelha característica. Forma um Rede cristalina hexagonal.

Safira 

É também um cristal de óxido de alumínio, mas com impurezas de titânio e ferro, responsáveis ​​por sua cor azul em vários tons. Como o rubi tem Estrutura hexagonal.

Jade

Pedra preciosa geralmente verde, tem Estrutura monoclínica E é composto de silicato de ferro-magnesium-calcio.

Topázio 

É incolor com um Estrutura ortorrômbica de fluoreto de alumínio-hidróxido-silicato.

Exercícios resolvidos

Exercício 1

Encontre a relação entre o parâmetro de rede e o raio atômico para uma rede cúbica F.

Pode servir a você: Teoria do Big Bang: características, estágios, evidências, problemas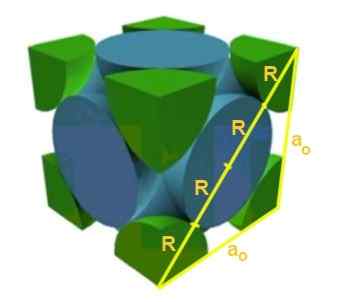

Solução: Em primeiro lugar, supõe -se que os átomos sejam representados como esferas todo o raio r em "contato" um com o outro, como mostrado na figura. Um triângulo retângulo é formado no qual é cumprido que:

(4 r)^2 = a^2 + a^2 = 2 a^2

Então você tem que o relacionamento de radio de borda é:

A/r = 4/√2

Exercício 2

Encontre a relação entre o parâmetro de rede e o raio atômico para uma rede cúbica I (centralizada no corpo).

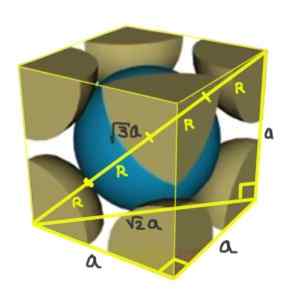
Solução: Os átomos devem ser representados como todas as esferas de raio r em "contato" entre si, como mostrado na figura.

Dois retângulos são formados um de hipotenusa √2a e o outro de hipotenusa √3a, como pode ser demonstrado usando o teorema de Pitagoreano. A partir daí, você tem para o relacionamento entre o parâmetro de rede e o raio atômico para uma rede cúbica I (centralizada no corpo) é:

A/r = 4/√3

Exercício 3

Encontre o fator de embalagem F para uma célula unitária de uma estrutura cúbica F (centradas cúbicas em faces) em que os átomos têm rádio e estão em "contato".

Solução: O fator de empacotamento F é definido como a razão entre o volume ocupado pelos átomos na célula unitária e o volume da célula:

F = vátomos / Vcélula

Como demonstrado acima, o número de átomos por unidade de célula de uma rede cúbica centrada em faces é 4, portanto o fator de embalagem será:

F = 4 [4πr^3/3] /[a^3] =…

… 4 [4πr^3/3]/[4r/√2]^3 = (√2) π/6 = 0,74

Referências

1. Estruturas de cristal Centro de recursos acadêmicos. [PDF]. Recuperado em 24 de maio de 2018, de: Web.IIT.Edu
2. Cristais. Recuperado em 26 de maio de 2018, de: pensamento.com
3. Pressbooks. 10.6 estruturas de latice em sólidos cristalinos. Recuperado em 26 de maio de 2018, de: OpenTextBC.AC
4. Ming. (30 de junho de 2015). Tipos de estruturas cristalinas. Recuperado em 26 de maio de 2018, de: CrystalVisions-Film.com
5. Helmestine, Anne Marie, Ph.D. (31 de janeiro de 2018). Tipos de 
6. Kittel Charles (2013) Física de Estado Sólido, Física da Matéria condensada (8ª edição). Wiley.
7. Khi. (2007). Estruturas cristalinas. Recuperado em 26 de maio de 2018, de: folk.Ntnu.Não
8. Wikipedia. Bravais Latices. Recuperado de: em.Wikipedia.com.