Definição convexa de polígono, elementos, propriedades, exemplos

A polígono convexo É uma figura geométrica contida em um plano que é caracterizado porque possui todas as suas diagonais dentro e seus ângulos medem menos de 180º. Entre suas propriedades estão as seguintes:

1) Consiste em n segmentos consecutivos, onde o último dos segmentos se junta ao primeiro. 2) Nenhum dos segmentos é cruzado de tal maneira que delimite o avião em um interior e outro exterior. 3) Cada um dos ângulos da região interna é estritamente menor do que um ângulo plano.

figura 1. Os polígonos 1, 2 e 6 são convexos. (Preparado por Ricardo Pérez).

Uma maneira simples de determinar se um polígono é convexo ou não é considerar a linha que passa por um de seus lados, o que determina dois semipans. Se em cada linha que passa por um lado, os outros lados do polígono estão no mesmo semiplano, é então um polígono convexo.

[TOC]

Elementos de um polígono

Cada polígono consiste nos seguintes elementos:

- Lados

- Vértices

Os lados são cada um dos segmentos consecutivos que compõem o polígono. Em um polígono, nenhum dos segmentos que o compõem pode ter uma extremidade aberta; nesse caso, haveria uma linha poligonal, mas não um polígono.

Os vértices são os pontos sindicais de dois segmentos consecutivos. Em um polígono, o número de vértices sempre é igual ao número de lados.

Se dois lados ou segmentos de uma cruz de polígono, então você tem um polígono cruzado. O ponto de travessia não é considerado um vértice. Um polígono cruzado é um polígono não convexo. Os polígonos acidentados são polígonos cruzados e, portanto, não são convexos.

Pode atendê -lo: geometria analítica

Quando um polígono tem todos os lados do mesmo comprimento, há um polígono regular. Todos os polígonos regulares são convexos. 

Polígonos convexos e não convexos

A Figura 1 mostra vários polígonos, alguns deles são convexos e outros não são. Vamos analisá -los:

O número 1 é um polígono de três lados (triângulo) e todos os ângulos internos são menores que 180º, portanto é um polígono convexo. Todos os triângulos são polígonos convexos.

O número 2 é um polígono de quatro lados (quadrilateral), onde nenhum dos lados é interceptado e também todos e cada um dos ângulos interiores é menor que 180º. É então um polígono convexo de quatro lados (quadrilateral convexo).

Por outro lado, o número 3 é um polígono de quatro lados, mas um de seus ângulos internos é maior que 180º, por isso não atende à condição de convexidade. Isto é, é um polígono não convexo que é chamado de côncavo quadrilateral.

O número 4 é um polígono de quatro segmentos (lados), dois dos quais são interceptados. Os quatro ângulos internos são inferiores a 180º, mas à medida que os dois lados cruzam, eles são um polígono cruzado não convexo (quadrilátero cruzado).

Outro caso é o número 5. Este é um polígono de cinco anos, mas como um de seus ângulos internos é maior que 180º, há um polígono côncavo.

Finalmente, o número 6, que também tem cinco lados, tem todos os seus ângulos internos inferiores a 180º, por isso é um polígono convexo de cinco anos (Pentágono Convexo).

Pode servir a você: Erro de amostragem: fórmulas e equações, cálculo, exemplos

Propriedades convexas de polígono

1- Um polígono não esmagado ou polígono simples divide o avião que o contém em duas regiões. A região interior e a região externa, sendo o polígono a fronteira entre as duas regiões.

Mas se o polígono também for convexo, existe uma região interna que está simplesmente relacionada, o que significa que levar dois pontos da região interna, ela sempre pode ser unida por um segmento que pertence à sua totalidade à região interna.

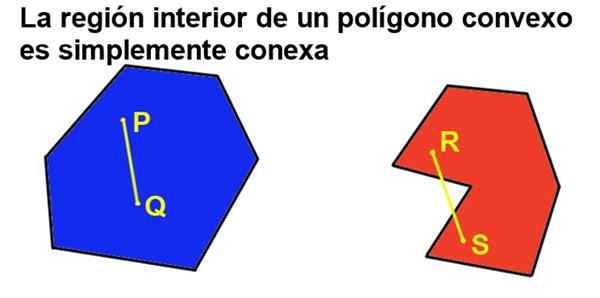Figura 2. Um polígono convexo está simplesmente relacionado, enquanto um côncavo não é. (Preparado por Ricardo Pérez).

2- Todo o ângulo interno de um polígono convexo é menor que um ângulo plano (180º).

3- Todos os pontos interiores de um polígono convexo sempre pertencem a um dos semi-definidos pela linha que passa por dois vértices consecutivos.

4- Em um polígono convexo, todas as diagonais estão totalmente contidas na região do polígono interno.

5- Os pontos interiores de um polígono convexo pertencem à sua totalidade ao setor angular convexo definido por cada ângulo interno.

6- Todo polígono no qual todos os seus vértices estão em circunferência é um polígono convexo chamado polígono cíclico.

7- Cada polígono cíclico é convexo, mas nem todo polígono convexo é cíclico.

8- Todo polígono não esmagado (polígono simples) que tem todos os seus lados de igual comprimento é convexo e é conhecido como polígono comum.

Diagonais e ângulos em polígonos convexos

9- O número total de diagonais de um polígono convexo de N lados é dado pela seguinte fórmula:

Pode atendê -lo: gráficos polybal

N = ½ n (n - 3)

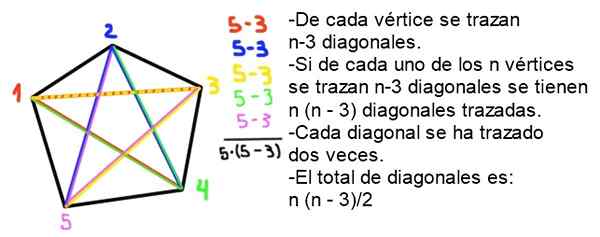
Demonstração: Em um polígono convexo de N lados de cada vértice, N - 3 diagonais são desenhadas, uma vez que o próprio vértice e os dois adjacentes são excluídos. Como existem n vértices, eles são desenhados no total de diagonais N - 2), mas cada diagonal foi desenhada duas vezes; portanto, o número de diagonais (sem repetição) é n (n -2)/2.

10- A soma dos ângulos internos de um polígono convexo de N lados é dado pelo seguinte relacionamento:

S = (n - 2) 180º

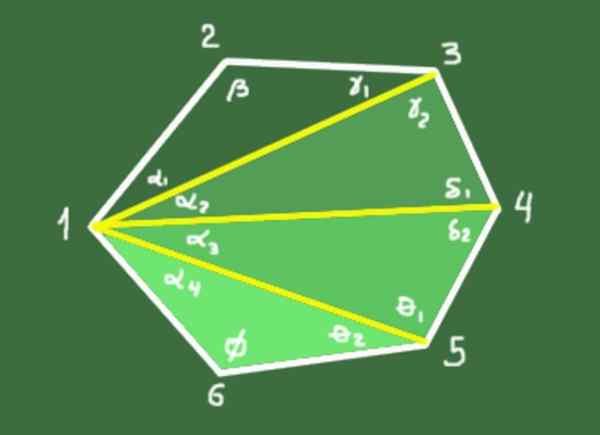
Demonstração: as diagonais N-3 são extraídas de um vértice que define triângulos N-2. A soma dos ângulos internos de cada triângulo é 180º. A soma total dos ângulos dos triângulos N-2 é (N-2)*180º, que coincide com a soma dos ângulos internos do polígono.

Exemplos

Exemplo 1

Hexágono cíclico, é um polígono de seis e seis vértices, mas todos os vértices estão na mesma circunferência. Todo o polígono cíclico é convexo.

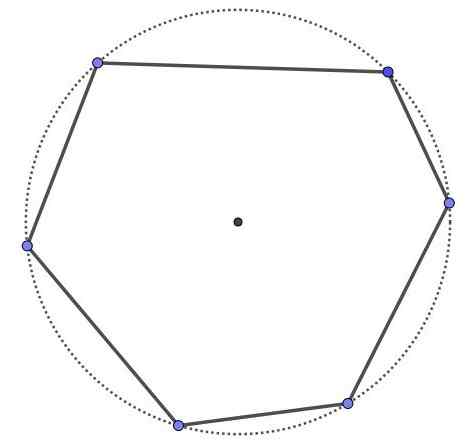Hexágono cíclico.

Exemplo 2

Determinar o valor dos ângulos internos de um Enegon regular.

Solução: Enegon é um polígono de 9 anos, mas também está regulando todos os seus lados e ângulos.

A soma de todos os ângulos internos de um polígono de 9 anos é:

S = (9 - 2) 180º = 7 * 180º = 1260º 

Mas existem 9 ângulos internos de igual medida α, portanto a seguinte igualdade deve ser cumprida:

S = 9 α = 1260º

De onde se segue que a medida α de cada ângulo interno do Enegon regular é:

α = 1260º/9 = 140º