O que é equilíbrio dinâmico? (Com exemplo)

Ele Equilíbrio dinâmico É o estado em que um objeto móvel é idealmente representado como uma partícula quando seu movimento é uniforme retilíneo. Esse fenômeno ocorre quando a soma das forças externas que atua é cancelada.

Geralmente acredita. Ou também para que um corpo esteja em equilíbrio, não deve haver força atuando.

figura 1. Este gato se move em equilíbrio dinâmico se o fizer com velocidade constante. Fonte: Pixabay.

Na verdade, o equilíbrio é a ausência de aceleração e, portanto, a velocidade constante é perfeitamente possível. O gato na figura pode estar se movendo sem aceleração.

Um objeto que possui movimento circular uniforme não está em equilíbrio dinâmico. Embora sua velocidade seja constante, há uma aceleração direcionada para o centro da circunferência que a mantém na trajetória. Esta aceleração é responsável por mudar adequadamente para o vetor de velocidade.

A velocidade nula é uma situação particular do equilíbrio de uma partícula, equivalente a afirmar que o objeto está em repouso.

Quanto a considerar objetos como uma partícula, é uma idealização muito útil ao descrever seu movimento global. Na verdade, os objetos móveis que nos cercam são compostos por um grande número de partículas cujo estudo individual seria complicado.

[TOC]

O princípio da superposição

Este princípio permite substituir a ação de múltiplas forças em um objeto por um equivalente chamado força resultante de força ou força líquida e que, neste caso, é nulo:

F1 +F2 +F3 +… . = Fr = 0

Onde forças F1, F2, F3 .. ., Fi são as diferentes forças que agem no corpo. A notação de Sumory é uma maneira compacta de expressá -la:

Enquanto uma força desequilibrada não intervir, o objeto pode ser mantido indefinidamente em movimento com velocidade constante, pois apenas uma força pode alterar esse panorama.

Em termos dos componentes da força resultante, a condição dinâmica de equilíbrio de uma partícula é expressa da seguinte forma: fx = 0; Fy = 0; Fz = 0.

Condições de rotação e equilíbrio

Para o modelo de partículas, condição fr = 0 é garantia de equilíbrio suficiente. No entanto, ao levar em consideração as dimensões do celular em estudo, existe a possibilidade de o objeto girar.

O movimento de rotação implica a existência de uma aceleração; portanto, os corpos rotativos não estão em equilíbrio dinâmico. A virada de um corpo precisa não apenas da participação de uma força, mas é necessário aplicar o site conveniente.

Para verificar, você pode colocar uma haste fina de comprimento em uma superfície livre de atrito, como uma superfície gelada ou um espelho ou vidro muito polido. Os saldos normais ao peso verticalmente e ao aplicar duas forças F1 e F2 da mesma magnitude, de acordo com o diagrama da figura a seguir, o que acontece:

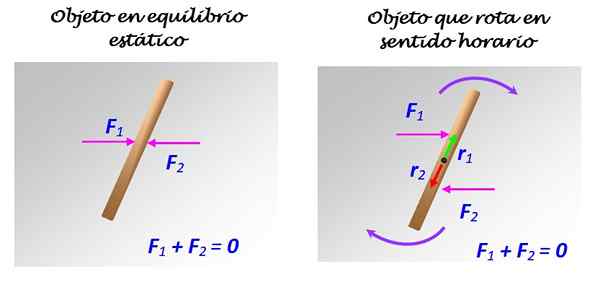Figura 2. Uma haste em uma superfície sem atrito pode ou não estar em equilíbrio, dependendo de como as forças 1 e 2 são aplicadas. Fonte: Self feito.

Se F1 e F2 se aplicarem como mostrado à esquerda, com uma linha de ação comum, a haste permanecerá em repouso. Mas se F1 e F2 se aplicarem como mostrado à direita, com diferentes linhas de ação, embora paralelas, ocorre uma rotação em um cronograma, ao redor do eixo que passa pelo centro.

Nesse caso, F1 e F2 constituem algumas forças ou simplesmente um casal.

Torque ou momento de força

O efeito do torque é produzir uma rotação em um objeto estendido, como a haste de exemplo. A magnitude do vetor no comando é chamada de torque ou também um momento de força. É indicado como τ e é calculado por:

τ = r x f

Nesta expressão F é a força aplicada e R é o vetor que vai do eixo de rotação até o ponto de aplicação da força (veja a Figura 2). A direção de τ é sempre perpendicular ao plano onde F e R mentam e suas unidades no sistema internacional são n.m.

Para o exemplo, a direção dos momentos produzidos por F1 e F2 é para o artigo, de acordo com as regras do produto vetorial.

Embora as forças se cancelem, seus torques não. E o resultado é a rotação mostrada.

Condições de equilíbrio para um objeto estendido

Estas são duas condições que devem ser atendidas para garantir o equilíbrio de um objeto estendido:

Exemplo resolvido

Você tem uma gaveta ou porta-malas que pesa 16 kg-f, que desliza através de um plano inclinado com velocidade constante. O ângulo de inclinação da cunha é θ = 36º. Responder:

a) Qual é a magnitude da força de atrito dinâmico necessária para o porta -mala deslizar com velocidade constante?

b) quanto é o coeficiente de atrito cinético?

c) Se a altura h do plano inclinado for de 3 metros, encontre a taxa de descida do porta -malas, sabendo que leva 4 segundos para alcançar o solo.

Solução

O porta -malas pode ser tratado como se fosse uma partícula. Portanto, as forças serão aplicadas em um ponto localizado aproximadamente em seu centro, no qual toda a sua massa pode ser assumida. É nesse ponto que a faixa será seguida.

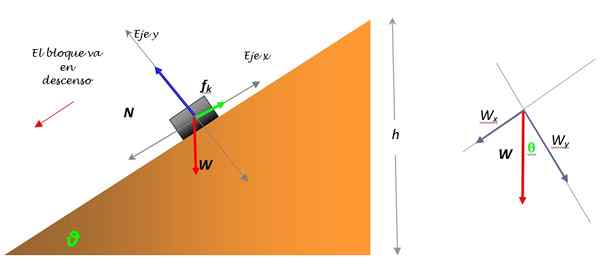Figura 3. Diagrama do corpo livre para o porta -malas que desliza ladeira abaixo e a decomposição do peso (à direita). Fonte: Self feito.

O peso w é a única força que não cai em um dos eixos de coordenadas e deve ser dividido em dois componentes: WX e WY. Esta decomposição é mostrada no esquema (Figura 3).

Também é conveniente passar o peso para as unidades do sistema internacional, para o qual é suficiente para se multiplicar por 9.8:

Wy = w.cosθ = 16 x 9.8 x cos 36º n = 126.9 n

Wx = w.Senθ = 16 x 9.8 x sin 36º = 92.2 n

Seção a

Em todo o eixo horizontal estão o componente horizontal do peso WX e a força de atrito dinâmica ou cinética da FK, que se opõe ao movimento.

Escolhendo o sentido positivo na direção do movimento, é fácil perceber que é WX responsável pelo bloco descer ladeira abaixo. E à medida que o atrito se opõe, em vez de escorregar rapidamente, o bloco tem a possibilidade de deslizar constantemente ladeira abaixo.

A primeira condição de equilíbrio é suficiente, pois estamos tratando o tronco como uma partícula, que é garantida na declaração que está em equilíbrio dinâmico:

Wx - fk = 0 (não há aceleração no endereço horizontal)

FK = 92.2 n

Seção b

A magnitude do atrito dinâmico é constante e é dado por fk = μk n. Isso significa que a força de atrito dinâmica é proporcional ao normal e a magnitude disso é necessária para conhecer o coeficiente de atrito.

Observando o diagrama do corpo livre, pode -se ver que no eixo vertical temos a força normal n, que a cunha exerce no porta -malas e é direcionada para cima. Ela é equilibrada com o componente vertical do peso wy. Selecionando como um sentido positivo e utilizando a segunda lei de Newton e os resultados do status do saldo:

N - wy = 0 (não há movimento ao longo do eixo vertical)

Portanto:

N = wy = 126.9 n

fk = μk n

μk = fk / n = 92.2 /126.9 = 0.73

Seção c

A distância total percorrida pelo tronco do topo da cunha até o solo é encontrada pela trigonometria:

d = h/sin 36º = 3/sin 36º m = 5.1 m.

Para calcular a velocidade, é usada a definição de movimento retilíneo uniforme:

V = d/t = 5.1 m/4 s = 1.3 m/s

Referências

1. Rex, a. 2011. Fundamentos da Física. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning. 120 - 124.
3. Serway, r., Vulle, c. 2011. Fundamentos da Física. 9na ed. Cengage Learning. 99-112.
4. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Física. Addison Wesley. 148-164.